大桩帽轨道梁不同支承条件的受力分析

陶桂兰，卜美飞

（河海大学港口海岸与近海工程学院，江苏 南京 210098）

1 问题的提出

随着装卸设备的大型化及码头向外海发展，为满足结构的使用要求及抵抗施工期的波浪作用，纵、横梁节点处的桩数增多，工程上常在节点处采用大桩帽结构，桩帽上搁置预制梁并现浇梁节点，因此梁的支座宽度较以往大大增加，有些码头轨道梁的支座宽度已达到梁中到中跨度的0.6倍左右[1]。JTJ267—98《高桩码头设计与施工规范》（以下简称98规范）在梁内力计算中，将纵梁简化为弹性支承连续梁或刚性支承连续梁计算，弹性支承连续梁法支座处采用点支承，无法考虑支座宽度的影响。现行JTS167-1—2010《高桩码头设计与施工规范》（以下简称2010规范），考虑到目前高桩码头的发展趋势，在规范中提出了轨道梁宽支座计算方法，采用支座内的分布弹簧模拟宽支座的影响。但宽支座梁的受力特性如何，新老规范不同支承条件对轨道梁内力的影响仍是工程界极为关心的问题。本文以某大桩帽码头为例，模拟高桩码头中的纵向轨道梁排架，利用Ansys软件对模型进行有限元模拟，得到纵梁在采用大桩帽时的一些受力特性，并对轨道梁不同支承条件下的受力特性进行了比较分析，以供类似工程设计参考[2-3]。

2 计算模型

2.1 工程概况

本文计算结构以上海某码头后门机轨道梁为例，纵梁全长78 m，共6个排架，排架间距12 m，两端各有3 m长的悬臂段，纵梁使用期截面尺寸为1.6 m×2.75 m，桩帽尺寸为6.3 m×5.4 m×2.1 m。纵梁及桩帽材料为混凝土C45，弹性模量E=3.35×104MPa，泊松比μ=0.167。桩基为钢管桩，桩自由长度为12.4 m，外径1.2 m，壁厚0.02 m，弹性模量E=2.1×105MPa，泊松比μ=0.3。每个桩帽下设有3根斜桩，斜桩倾斜度为6∶1。轨道梁结构示意图见图1。

图1 轨道梁结构示意图（单位：m）

2.2 计算模型

本文考虑《98规范》及《2010规范》中轨道梁的3种支承方式及宽支座梁空间有限元模型对宽支座轨道梁进行计算分析，计算模型均采用ANSYS有限元软件建模。

1）刚性点支承连续梁模型

该计算模型中的轨道梁采用beam188单元，支座处节点的竖向自由度约束，3个转动自由度自由。有限元模型见图2。

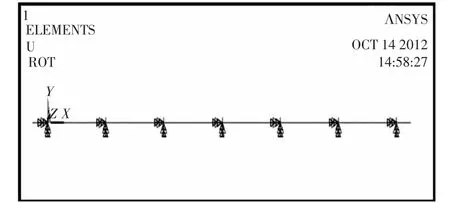
图2 刚性点支承连续梁有限元模型图

2）弹性点支承连续梁模型

模型中的轨道梁采用beam188单元，支承处用弹簧单元combin14模拟弹性点支承，弹簧与梁单元连接点处进行节点耦合，弹簧底端全部固定。弹簧常数取所在支座处的刚性系数，计算得k=1.303×106kN/m。有限元模型见图3。

图3 弹性点支承连续梁有限元模型图

3）分布弹性支承计算模型

当以支座宽度范围内有限个等间距布置的弹簧代替均匀分布弹簧时，单个弹簧的刚性系数可按下式计算：

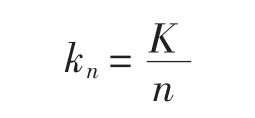
式中：kn为单个弹簧刚性系数，kN/m；K为支座竖向刚性系数，kN/m，取桩帽在支座中心处产生单位竖向位移时所需竖向作用力的数值；n为支座宽度范围内等间距布置的弹簧个数。

模型中的纵梁选取beam188单元，选取弹簧单元combin14来模拟弹性支承，每个支座宽度范围内均匀布置28个弹簧，每个弹簧常数相同。经计算取支座竖向刚性系数为k=1.303×106kN/m，可得单个弹簧常数为k=46 530 kN/m。弹簧与梁单元连接点处进行节点耦合，弹簧底端全部固定，模型有限元图见图4[4-5]。

4）空间有限元计算模型

为便于比较不同计算模型对内力的影响，本文同时建立了纵向排架空间有限元计算模型。纵梁采用beam188单元，桩帽选用实体单元solid45模拟，桩基采用管单元pipe16，桩与桩帽采用固接连接，桩端与土之间弹性嵌固，经计算，嵌固深度取4.6 m。梁单元和桩帽实体单元连接处采用节点耦合，桩端与土之间用弹簧单元combin14来模拟，桩与弹簧单元连接点处除桩轴向自由度外，其他自由度全部约束，弹簧底端固接。有限元模型见图5[4-5]。

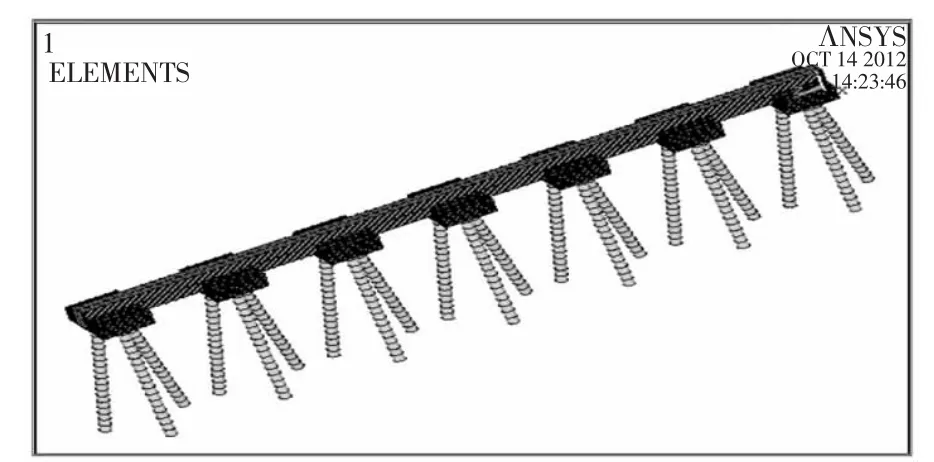
图5 纵向排架空间有限元模型图

3 计算结果分析

计算时采用均布荷载，荷载值取q=151kN/m。各计算模型弯矩、剪力图对比见图6、图7，考虑到模型以及荷载的对称性，文中只给出半梁弯矩、剪力图。（图中坐标轴黑线部分表示桩帽段）：

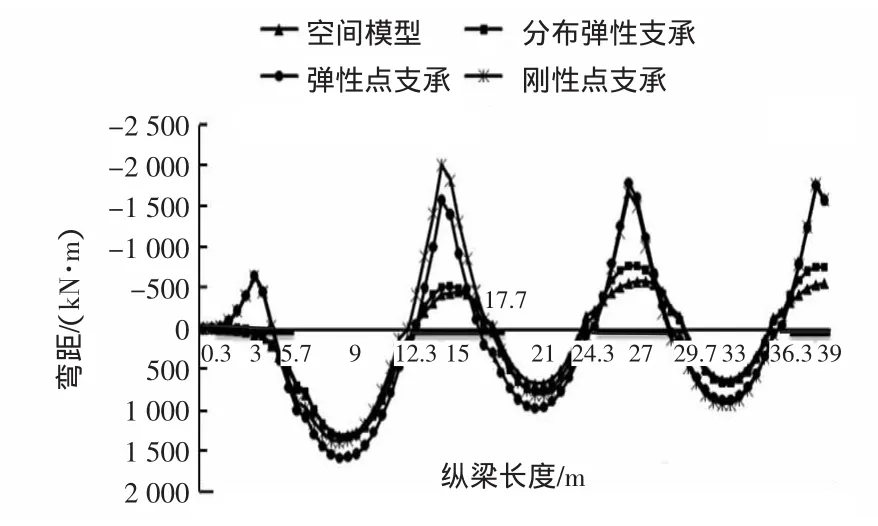
图6 不同计算模型轨道梁弯矩比较

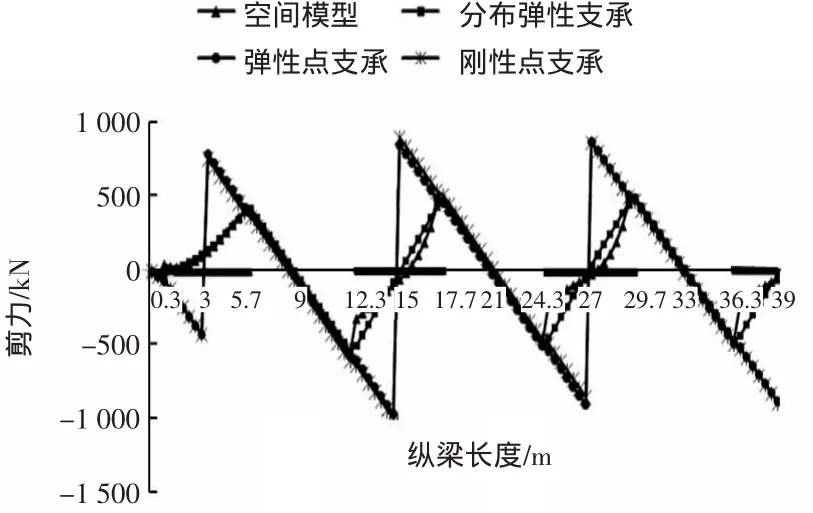
图7 不同计算模型轨道梁剪力比较

各模型的最大正负弯矩以及最大剪力见表1。

3.1 弯矩分布特性

由弯矩图及表1可知：弹性点支承连续梁计算所得的最大负弯矩小于刚性点支承连续梁，而最大正弯矩大于刚性点支承连续梁。弹性点支承模型计算所得的最大正弯矩、最大负弯矩、最大剪力要比分布弹性支承计算所得结果要大的多，特别是最大负弯矩达到2.3倍，表明支承宽度对连续梁的内力有明显的削峰作用，特别是最大负弯矩。

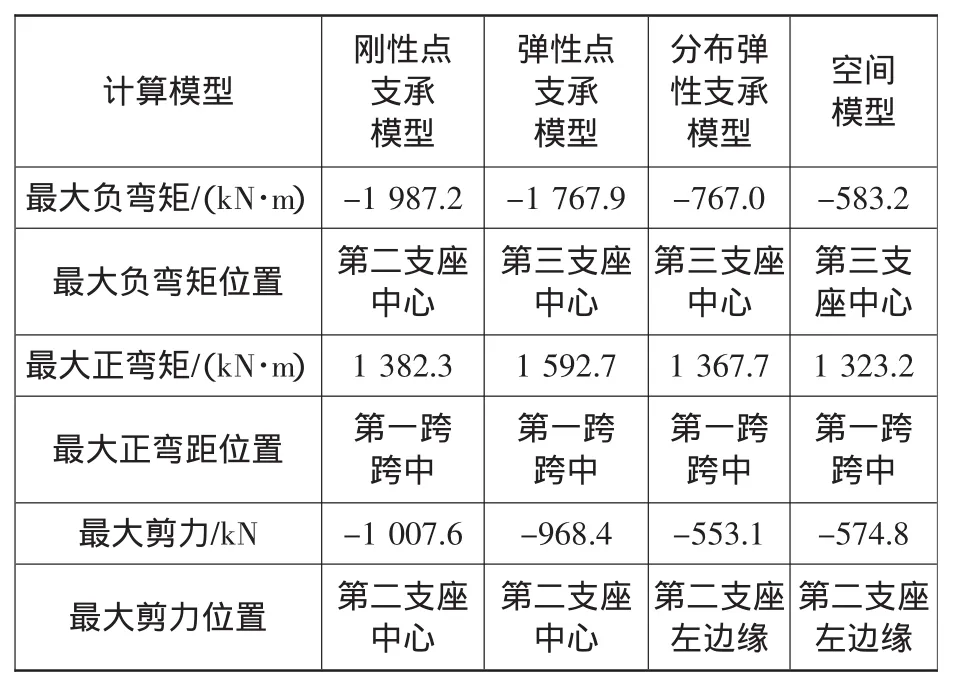
表1 各计算模型最大正负弯矩以及剪力

从支座边缘处的弯矩比较可以看出，两种点支承模型与分布弹性支承模型以及空间模型在支座左边缘处的弯矩符号完全相反，表明如果桩帽宽度比较大时，对点支承模型进行支座处弯矩削峰后取支座边缘处弯矩作为控制弯矩有可能产生较大的误差。

从分布弹性支承与空间模型弯矩图比较可知，两种模型的计算结果比较接近，本例计算结果表明，空间模型计算所得支座边缘处的最大负弯矩比分布弹性支承模型略大，而支座中心处的最大负弯矩比分布支承模型略小，即空间模型的支座弯矩在支座范围内更为均匀。

3.2 剪力分布特性

从剪力值计算结果可以看出，刚性点支承模型计算所得最大剪力大于其它3种模型，刚性点支承模型支座边缘处的剪力值最大，空间模型和分布弹性支承模型计算结果比较接近，4种计算模型支座边缘处的剪力差别不大。

3.3 支座反力分布特性

分布弹性支承、空间模型各支座反力分布见图8，考虑到结构的对称性，文中给出前四个桩帽处的支座反力分布图。

从各支座反力分布图可知，分布弹性支承与空间模型支座处反力分布差距较大，分布弹性支承支座处的反力分布基本呈均匀分布，而空间模型支座两端反力较大，支座中间反力较小，呈抛物线分布。支座反力分布应与支承模型假定有关，有待于进一步讨论。

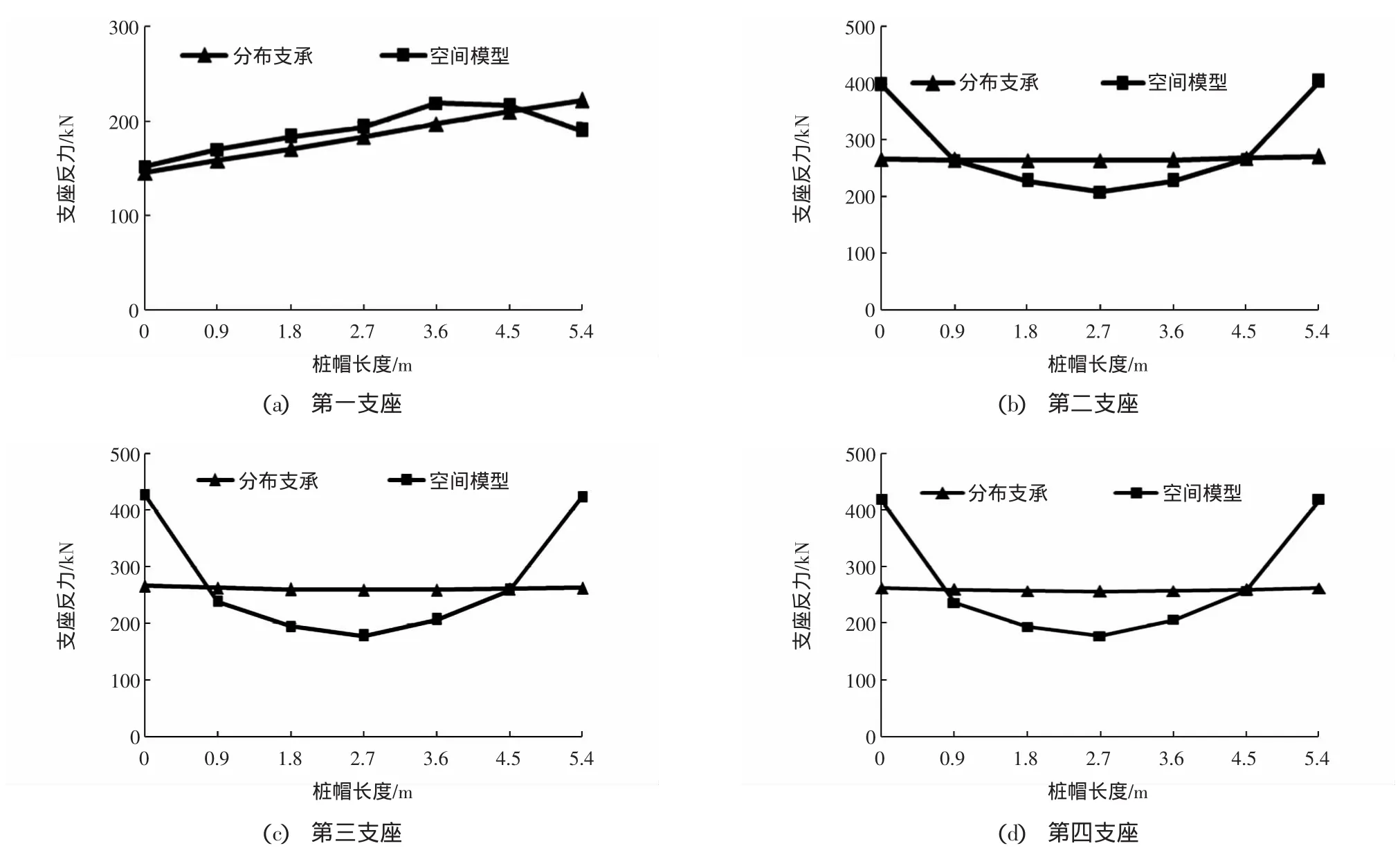
图8 各支座反力分布图

4 主要结论

本文以某宽支座梁为例，通过ANSYS软件对宽支座梁的4种模型：弹性点支承，刚性点支承，分布弹性支承以及空间模型进行有限元模拟，得出不同模型下的连续梁内力以及支座反力的分布特性，并对不同模型的计算结果进行比较，得到以下主要结论：

1）对于大桩帽轨道梁，按弹性点支承模型及刚性点支承连续梁模型计算弯矩与宽支座梁分布模型计算其支座边缘处的弯矩有较大差异，对宽支座梁采用弹性点支承模型连续梁计算弯矩后再削峰的方法将可能产生较大的误差。

2）计算表明支座宽度对连续梁的内力有明显的削峰作用，特别是最大负弯矩，因此对大桩帽梁计算时有必要考虑宽支座的影响。

3）对于大桩帽梁，按弹性和刚性点支承连续梁模型计算支座中心截面剪力与分布弹性支承模型及空间模型计算值差异较大，支座边缘处剪力值与分布弹性支承模型及空间模型的计算结果比较接近。

4）分布弹性支承模型与空间模型的内力计算结果比较相近，但空间模型与分布弹性支承模型在各支座处的反力分布相差较大，对于支座反力计算模型，有待于进一步讨论。

[1] 周伟才.大桩帽码头排架计算方法及模型试验研究[D].南京：河海大学，2005.

[2] 曹称宇.宽支座条件下梁的内力计算研究[D].南京：河海大学，2005.

[3] 周伟才，陶桂兰.考虑节点域和剪切变形影响的高桩码头横向排架的内力计算[J].水利水运工程学报，2005（1）：56-59.

[4] 王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007：230-407.

[5] 陆东汉.用宽支承方式计算高桩梁板式码头上的轨道梁[J].水运工程，2003（12）：36-39.