桩基托梁式挡土墙在黄土路堑中的应用研究

赵如意

(中铁第一勘察设计院集团有限公司, 西安 710043)

桩基托梁挡土墙是挡土墙与桩基础[1]的组合形式,由托梁相连接,最早于20世纪60年代在成昆铁路陡峻山坡的路堤处采用[2]。据统计,成昆铁路有铁西、白果、拉白等8处桩基托梁挡土墙,共长283.23 m。实践表明,该型挡土墙使用效果明显,技术可靠,投资节省。与常规的扩大基础挡墙方案比较,圬工量可省35%,挖基量可省70%。由于其突出的优点,后被宝成铁路增建第二线、达成铁路东段、广梅汕铁路等多条线路采用。桩基托梁挡土墙尽管在工程上进行了一定的应用,但由于结构中存在挡土墙、托梁、路基及地基土体、桩基等多种结构,使得其作用机理非常复杂,挡土墙、托梁、桩基、周围土体四者之间作用力大小和传递途径不明确[3]。此外,目前采用的桩基托梁挡土墙也主要用在山区铁路陡峻山坡、隧道洞口等不同位置,但在黄土地区却较少见文献报道。基于此,本文主要结合黄陵—韩城—侯马铁路建设工程实践,进行在黄土地区设计桩基托梁挡土墙工程实践研究。

1 工程概况

1.1 概述

黄陵—韩城—侯马铁路位于陕西省延安市、渭南市及山西省运城市、临汾市境内,线路全长204.58 km,线路正线设计时速120 km,Ⅰ级重型电气化铁路。北塬至芝阳为新建双线段,南永宁至金水沟上行联络线为单线,南永宁至金水沟上行联络线于DK54+733.12位置处上跨正线,与正线斜交37°,因正线净空要求,只能设置箱形桥,其他桥型满足不了正线净空要求。为保证桥两端联络线路基稳定,并与箱形桥两侧顺接,于箱形桥两侧设置胸坡基本垂直的挡土墙进行收坡,墙高10 m左右。结合工程实际情况,经多方案比选试算,本工程最终选定采用托梁式挡土墙结构,通过对所选定的桩基托梁式挡土墙进行计算设计,并与三维有限元仿真模拟结果相对比,为今后的此类设计提供参考。

1.2 地质特征

线路沿线大面积分布第四系黄土,本工程地层岩性从地表向下描述如下[4-6]：黏质黄土(Q3eol3)：浅棕黄色,厚度21.9～26 m,土质均匀,夹有钙质网膜及零星姜石,硬塑,Ⅱ级普通土,σo=150 kPa；黏质黄土(Q2eol3)：浅棕黄色,厚度大于15 m,土质均匀,夹有钙质网膜及零星姜石,硬塑,Ⅱ级普通土,σo=200 kPa；地表水不发育,钻孔深度内为揭露地下水,水质对工程无影响；场地黄土湿陷类型自重,湿陷等级Ⅳ级,湿陷土层厚22～29.3 m。

挡土墙墙背填料设计参数[7]:γ=19 kN/m3,φ=35°,摩擦系数f=0.6。衡重式挡土墙截面尺寸：墙高10 m,墙胸坡为1∶0.05,顶宽为0.5 m,上墙墙背坡为1∶0.40,下墙墙背坡为1∶0.25,承台宽度为1.79 m,墙体材料采用C25片石混凝土。

桩基地基设计参数[8,9]：地基水平比例系数4 200 kPa/m2，竖向比例系数10 000 kPa/m2。

1.3 托梁式挡土墙结构形式

挡土墙为路堑衡重式挡土墙,桩基设双排桩[10-11],具体结构形式如图1所示。

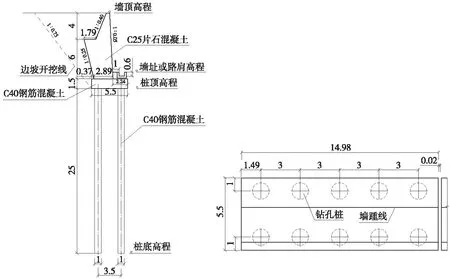
图1 托梁式挡土墙结构布置(单位：m)

2 设计方案计算分析

2.1 解析计算

基于挡土墙、托梁和桩基三者的受力特点、相互作用关系,以及考虑到挡土墙所受土压力等比较复杂。且根据规范,对于桩基托梁挡土墙,桩的设计是关键。因此,限于篇幅,这里采用如图2所示模型重点计算桩基础的受力。

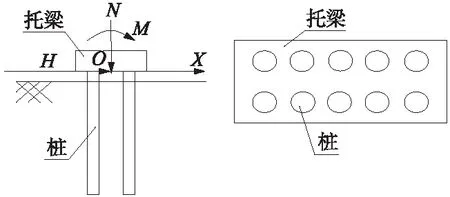
图2 桩基础受力分析的计算模型

其中,衡重式挡土墙可根据《铁路路基支挡结构设计规范》设计。当上部结构确定后,即可计算出墙底作用到托梁的竖向力N、水平力H和竖向力距托梁原点的偏心距e,挡墙对托梁原点处的弯矩M=eH。

假设托梁底板为刚性,用地基系数法的基本方法[12],可建立下列方程

(1)

式中γba、γaa、γβa——托梁底板产生单位水平位移时,所用桩顶产生的竖向反力之和、水平反力之和以及它们对坐标原点O的反弯矩之和,分别以kN/m、kN/m和kN·m /m计。

γbb、γab、γβb——托梁底板产生单位竖向位移时,所用桩顶产生的竖向反力之和、水平反力之和以及它们对坐标原点O的反弯矩之和,分别以kN/m、kN/m和kN·m /m计。

γbβ、γaβ、γββ——托梁底板绕O点产生单位转角时,所用桩顶产生的竖向反力之和、水平反力之和以及它们对坐标原点O的反弯矩之和,分别以kN/rad、kN/rad和kN·m /rad计。

上式中系数采用下列诸公式计算

γba=0；γaa=∑ρ2;γbβ=∑-ρ3;

γbb=∑ρ1;γab=γba;γβb=∑ρ1x;

γbβ=γβb;γaβ=γβa;γββ=∑(ρ1x2+ρ4)。

式中x——桩的顶点的坐标距,m；

ρ1——当托梁底板沿桩轴线方向产生单位位移时,所引起桩顶面处的轴向力,kN/m；

ρ2——当托梁底板沿垂直桩轴线方向产生单位横向位移(而无转角)时,所引起桩顶面处的横向力,kN/m；

ρ3——当托梁底板沿垂直桩轴线方向产生单位横向位移(而无转角)时,所引起桩顶面处的弯矩,kN·m /m；或当托梁底板顺桩顶面弯矩力方向产生单位转角(无横向位移)时,所引起桩顶面处的横向力,kN/rad；

ρ4——当托梁底板顺桩顶面弯矩方向产生单位转角(而无横向位移)时,所引起桩顶面处的弯矩,kN·m /rad。

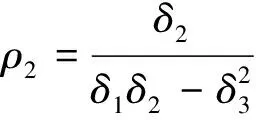
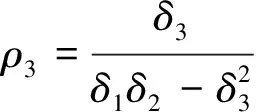
上面诸式中的δ1、δ2、δ3按下式求算

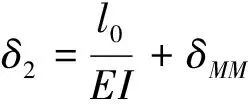
式中δ1、δ3——当桩顶作用单位横向力H=1时,桩顶的横向位移和转角,分别以m/kN和rad/kN计；

δ3、δ2——当桩顶作用单位力矩M=1时,桩顶的横向位移和转角,分别以m/kN·m和rad/ kN·m计；

δQQ、δMQ——按照地基系数法计算,当地面或局部冲刷线处作用单位横向力Q0=1时,桩在地面或局部冲刷线处的横向位移和转角,分别以m/kN和rad/kN计；

δQM、δMM——按照地基系数法计算,当地面或局部冲刷线处作用单位力矩M0=1时,桩在地面或局部冲刷线处的横向位移和转角,分别以m/kN·m和rad/kN·m计。

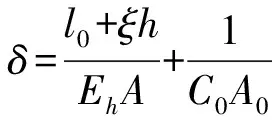
解方程(1),求出a、b、β后,图2中任一根桩顶的内力按下式计算

Ni=(b+βx)ρ1

Qi=aρ2-βρ3

Mi=βρ4-aρ3

求出Ni、Qi和Mi之后,可按地基系数法求得桩身任一截面的弯矩My、剪力Qy和桩侧土的横向应力σx。

对于本工点：托梁采用C40钢筋混凝土,高1.5 m,宽为5.5 m,长为14.98 m；力矩：M=2 250 kN·m；水平力：H=3 750 kN；桩身采用C40钢筋混凝土,桩为圆形截面:φ1.0 m；横向桩间距3.5 m；纵向桩间距3.0 m；桩长25.0 m；经过计算，承台水平位移a=4.58 mm,竖向位移2.00 mm,转角0.000 20 rad；内侧桩顶轴力1 567.68 kN,外侧桩顶轴力1 896.80 kN。桩基础单根桩的内力如图3所示。

图3 桩基础单根桩的内力图

2.2 有限元分析

根据桩基托梁挡土墙的受力特点,桩基托梁挡土墙计算长度沿纵向取14.98 m,即两伸缩缝间的长度,采用三维有限元仿真模拟。路基填土考虑弹塑性、用D-P模型,桩基托梁结构采用实体模型,荷载通过耦合施加在托梁顶面,挡土墙底部和左侧土体各取2～3倍墙高作为计算域地基,计算参数采用现场实测参数。计算结果如图4所示。

图4 桩基托梁的横向位移及托梁底面最大主应力

从图4中可以看出，通过有限元计算,托梁承台的水平位移为4.318 mm,小于理论计算时的4.58 mm。桩基和托梁的连接部位有较强的应力集中问题,最大拉应力出现在承台的底部,托梁结构中的最大拉应力0.318 MPa,小于C40混凝土的抗拉强度值1.71 MPa。

图5给出了单桩随桩深弯矩与剪力变化,曲线的变化规律整体与前面解析计算结果相似,但有一定的差异。理论计算时,在桩身15 m的位置时弯矩和剪力达到较小值,而有限元分析结果显示,弯矩在整个桩身位置都较大,剪力在10 m后达到较小值,桩顶最大弯矩342.04 kN·m,最大剪力212.10 kN,均小于解析计算的801 kN·m和375 kN。引起这种差异的主要原因是，理论计算时将桩简化为一端固结的悬臂梁和一端固结的弹性地基梁,悬臂部分没有考虑土体的支承作用,偏于保守。

图5 单根桩的弯矩及剪力图

综上可以看出,采用解析计算方法和有限元方法对于桩基托梁挡土墙均能取得较一致的计算结果,但从对比来看,解析计算结果偏于保守。

3 设计参数影响分析

3.1 土体参数的影响分析

考虑到土体参数的复杂性及确定其真值的困难性,本文采用3组土体参数,分析对比土体参数的变化对计算分析结果的影响(图6)。

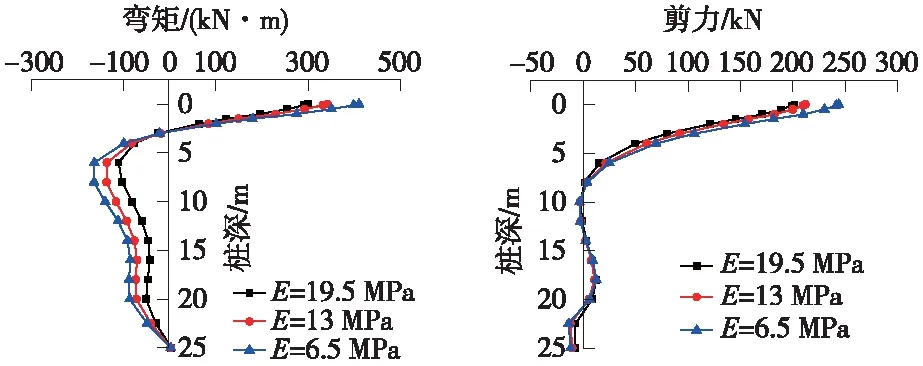
图6 土体参数的影响分析

由图6可知,改变土层参数,对桩基托梁挡土墙受力有一定影响,但规律基本一致。3种情况(土体模量分别为19.5、13、6.5 MPa),沿桩轴线桩身最大剪应力和最大弯矩均出现在桩顶位置处,最大剪应力分别为201.55、212.10、243.97 kN,最大弯矩分别为300.06、342.04、410.49 kN·m。随着土体模量的减小,剪力分别增大了5.23%与21.05%,弯矩分别增大了13.99%与36.80%。由此可见,地基土体参数的变化对桩基托梁挡土墙的受力影响非常敏感。黄土属于特殊土体,各地区土质属性差异较大,且随降雨等环境因素变化其力学性质变化也较大,因此建议在黄土地区使用桩基托梁挡土墙结构时应对土体参数的确定给予重点关注。

3.2 桩顶水平荷载的影响分析

当土体模量为13 MPa,受到的水平荷载为H=1 875、3 750、5 625 kN时,桩基托梁挡土墙结构的受力如图7所示。

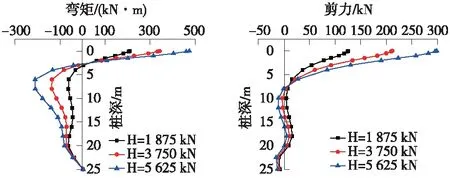
图7 桩顶水平荷载对桩基受力的影响分析

由图7可知,对于不同的桩顶水平荷载,沿桩轴线桩身最大剪应力和最大弯矩均出现在桩顶位置处,最大剪应力分别为125.46、212.10、298.73 kN,分别增大了69.06%、138%；最大弯矩分别为210、342.04、474.08 kN·m,分别增大了62.88%、126%。由此可见,施加在桩基托梁上的水平力对结构的影响非常显著。而水平力的大小与上部挡土墙的结构形式、高度、路基填料性质等密切相关。因此,建议在进行桩基托梁挡土墙设计时,对上部挡土墙的方案确定应给予重视,这也是决定桩基配筋等工程量的直接因素,进而对工程造价有很大影响。

3.3 桩顶弯矩的影响分析

当土体模量为13 MPa,受到的弯矩为M=1 125、2 250、3 375 kN·m时,桩基托梁挡土墙结构的受力如图8所示。

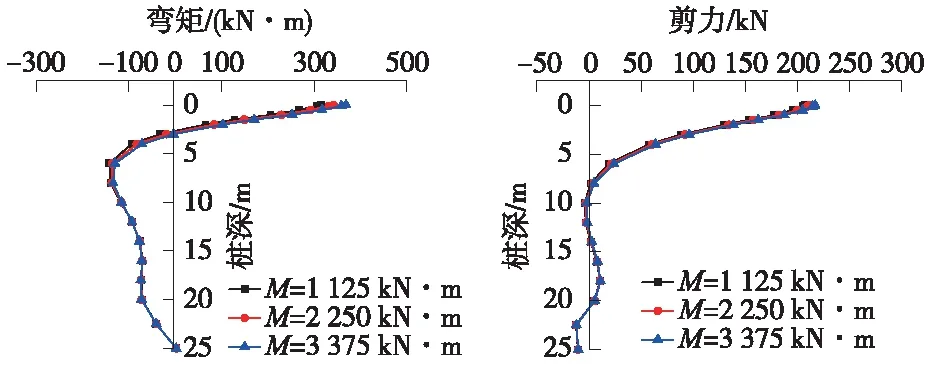
图8 桩顶弯矩对桩基受力的影响分析

由图8可知,对于不同的桩顶弯矩荷载,沿桩轴线桩身最大剪应力和最大弯矩均出现在桩顶位置处,最大剪应力分别为207.22、212.10、216.98 kN,分别增大了2.35%、4.71%；最大弯矩分别为315.43、342.04、368.65 kN·m,分别增大了8.44%、16.87%。由此可见,桩顶的弯矩变化对桩基托梁挡土墙的剪力影响较小,而对弯矩有一定的影响。

综合以上分析,地基土体参数的变化对桩基托梁挡土墙的受力影响非常敏感。在地基土体参数确定后,桩顶水平荷载的变化对结构的影响非常显著,桩顶弯矩的变化对桩基托梁挡土墙的弯矩有一定的影响,而对剪力影响较小。

4 结论及建议

结合黄陵—韩城—侯马铁路建设工程实践,对在黄土地区采用桩基托梁挡土墙进行了比较系统的设计研究,初步得到如下结论。

(1)采用解析计算方法和有限元方法对于桩基托梁挡土墙均能取得较一致的计算结果,但从相对比来看,解析计算结果偏于保守。设计时,应从工程安全出发,采用解析计算方法进行设计,并采用有限元方法对设计结果进行验证和优化。

(2)对土体参数、桩顶水平荷载、弯矩等设计参数进行了计算分析,结果表明土体参数与桩顶水平荷载对结构的影响非常敏感,而弯矩变化对结构的影响有限。

(3)基于黄土的特殊性,在采用桩基托梁挡土墙时应给予重点关注。考虑到桩顶水平荷载主要是由结构上部的挡土墙所产生,因此,在进行桩基托梁挡土墙设计时,对上部挡土墙方案的选择应予高度重视,在本文所述工程的设计中,上部挡土墙采用衡重式,墙胸坡1∶0.05,墙尺寸计算时,考虑挡土墙与桩基托梁的一体化,取较大的摩擦系数,以减小墙的断面尺寸；并将挡土墙的重心位置与桩基托梁的偏心位置布置在一条垂直线上,以减小桩基托梁承受的弯矩。

[1] 徐健强.黄土陡坡桥梁桩基础设计[J].铁道标准设计,2011(9):40-42，47.

[2] 李海光.新型支挡结构设计与工程实例[M].北京：人民交通出版社,2004．

[3] 孔德惠,孔书祥.桩基挡墙在既有铁路路基加固中的应用[J].铁道建筑,2008(4):50-52．

[4] 张全锋,李玉章.黄土特性及处理方法研究[J].中国勘察设计,2010(11):59-62．

[5] 王家鼎,腾志宏,王煜,韩晓盟.新建郑州—西安高速铁路黄土地层及其特征[J].西北大学学报,2008(5):795-800．

[6] 李华明,蒋关鲁,吴丽君,王智猛.黄土地基动力沉降特性试验研究[J].岩土力学,2009(8):2220-2224．

[7] 甘善杰,彭炳芬.不同计算方法对挡土墙设计的影响分析[J].高速铁路技术,2012(5):46-49．

[8] 李俊,强士中,李小珍.地基系数的比例系数m的确定[J].铁道标准设计,2004(11):83-85．

[9] TB10025—2006 铁路路基支挡结构设计规范[S].北京：中国铁道出版社,2006．

[10] 李黎.客运专线弹性地基梁桩基布置方案研究[J].铁道标准设计,2007(2):63-65．

[11] 崔俊杰,韩志霞.排桩挡土墙的设计及有关问题探讨[J].铁道标准设计,2006(11):13-15．

[12] 铁道部第三勘测设计院.铁路工程设计技术手册桥梁地基和基础[M].北京：中国铁道出版社,1996.