线路纵向阻力形式对桥上无缝线路计算影响

2013-01-17魏贤奎熊震威

铁道标准设计 2013年10期

刘浩,魏贤奎,熊震威,王平

(西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

线路纵向阻力是抵抗钢轨伸缩、防止线路爬行的主要因素之一,也是桥上无缝线路计算的一个重要参数[1-2]。目前,研究桥上无缝线路线桥纵向相互作用规律时,常采用的线路阻力形式有常阻力、双线性及幂指数型,我国《新建铁路桥上无缝线路设计暂行规定》采用常阻力形式,国际铁路联盟《梁轨相互作用计算的建议》(UIC 774-3)建议采用双线性阻力形式。在计算桥上无缝线路时,选取不同线路阻力形式,计算的结果可能不同,因此有必要分析不同线路阻力形式对其的影响。本文选取不同线路阻力形式,对简支梁桥上有砟轨道无缝线路进行计算分析。

1 线路纵向阻力形式

1.1 常阻力形式

采用常量阻力对桥上无缝线路附加力进行迭代计算时,依据《新建铁路桥上无缝线路设计暂行规定》[3],常量阻力取值见表1。

1.2 双线性阻力形式

有砟道床纵向阻力包括轨枕与道床间的摩擦阻力和轨枕盒内道砟抗推力,道床纵向阻力与轨枕类型及道砟密实程度、材质、颗粒级配、道床断面形状等有关[4]。依据《铁路无缝线路设计规范(送审稿)》规定[5],在计算桥上无缝线路时,采用的道床纵向阻力为双线性的,即梁轨位移小于某一位移时,线路纵向阻力与位移成线性关系,当位移大于或等于此位移量时,线路纵向阻力为常量,取值如图1所示。

轨面有载r=7.5z

轨面无载r=12z(1)

式中,r为钢轨纵向位移阻力，kN/m/线;z为梁轨相对位移,mm;轨面有无荷载，z>2 mm时均取为2 mm。线路纵向阻力与位移关系曲线见图1。

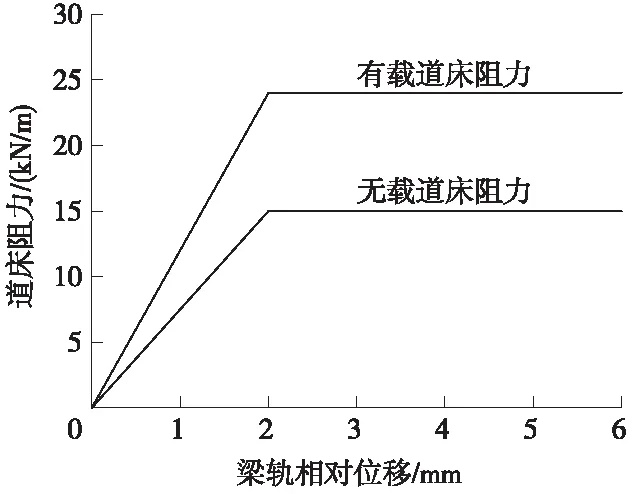
图1 有砟轨道道床纵向阻力

1.3 幂指数型阻力形式

试验表明,混凝土枕位移小于2 mm时,道床纵向阻力呈抛物线状增长,此时道床处于弹塑性工作范围,位移超过该值之后,纵向阻力的增长趋缓[6-7]。为了便于数值迭代法求解,根据实验测试数据拟合并计算出线路纵向阻力与位移的关系曲线。如图2所示。

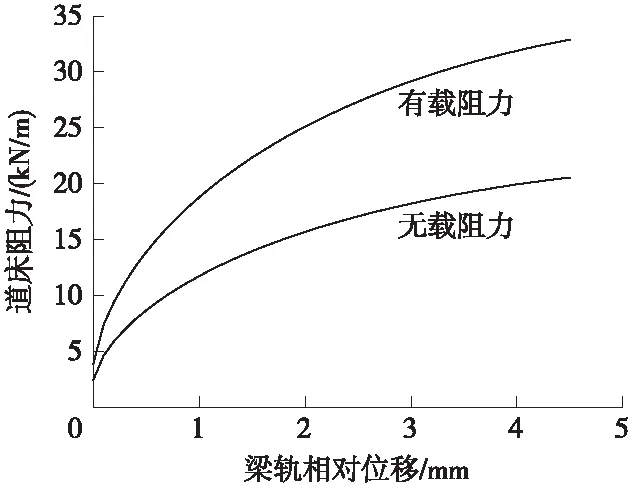
图2 幂指数型线路纵向阻力曲线

2 计算背景

2.1 计算模型

基于桥上无缝线路梁轨相互作用机理及轨道、桥梁的结构受力特点,建立线桥墩一体化计算模型[8-10],见图3。在该计算模型中,采用弹簧单元模拟线路纵向阻力。

图3 线桥墩一体化计算模型

2.2 计算参数

以简支梁桥为例,桥梁跨数为10跨,跨度分别取20、24、32 m和48 m,固定支座位于简支梁左边,在桥梁边跨两侧分别取112 m长的路基。梁体结构为预应力混凝土简支箱梁,梁高3.09 m,梁截面惯性矩为11.285 m4,桥台纵向水平刚度取3 000 kN/cm/线,在计算跨度为20、24 m和32 m简支梁时,桥墩纵向刚度取200 kN/cm/线,计算48 m简支梁时,取为500 kN/cm/线[11]。桥上铺设单线有砟轨道无缝线路,不设钢轨伸缩调节器。

因桥梁竖向抗弯刚度较大,由于荷载作用而产生的挠曲力小于因温度作用而产生的伸缩力,挠曲附加力在钢轨强度检算中不起控制作用,基于挠曲力与伸缩力不叠加考虑的原则,本文不计算挠曲力。

2.3 计算工况

在计算线路附加纵向力时,共分为3种工况：工况1采用的阻力形式为常量阻力,工况2为双线性阻力,工况3为幂指数型阻力。各工况除线路纵向阻力形式不同外,其余计算参数均相同。

3 计算结果及分析

3.1 伸缩力计算

规范规定：计算伸缩附加力时,混凝土有砟梁温度差取为15 ℃。桥梁跨度分别取20、24、32 m和48 m,分析线路阻力形式在不同温度跨度下对伸缩力的影响。计算结果如图4、图5所示,以钢轨受压为正。

图4 32 m简支梁钢轨附加伸缩力分布

图5 钢轨最大伸缩力对比

由计算结果可以看出,对于同一跨度的32 m简支梁,采用常阻力形式进行计算时,钢轨最大伸缩附加力为11.96 MPa,双线性阻力形式下钢轨伸缩力最大值为14.82 MPa,幂指数型计算结果为17.85 MPa。不同温度跨度下各线路阻力形式计算得到的钢轨伸缩力最大值见表2。

表2 钢轨伸缩力最大值 MPa

由计算结果得：当温度跨度相同时,3种线路阻力形式计算得到的钢轨伸缩力分布规律形同,只是大小不同,其中常阻力最小,幂指数型最大,双线性次之。桥梁温度跨度较小时,常量阻力和双线性计算结果相近,幂指数型较大,随着桥梁温度跨度的增加,双线性与幂指数型阻力计算结果越来越接近,而常量阻力与两者差别逐渐增大。这主要是因为在桥梁温度跨度比较小时,梁轨相对位移较小,常量阻力和双线性极限阻力取值比较接近,而幂指数型取值较大,但随着温度跨度的增加,梁轨相对位移大于2 mm时,双线性阻力和幂指数型极限阻力值相差不大,而常量阻力极限阻力仍然按测试值的0.5～0.8倍取值,导致计算结果偏小。由此可以预见，随着我国大跨度桥梁的出现,在检算时若仍按照常阻力形式取值时,会低估钢轨伸缩附加力的值。

3.2 制动力计算

制动力计算时,采用32 m简支梁,计算列车制动力时轨面摩擦系数取为0.164,荷载类型为中-活载,荷载从左至右入桥,全桥制动。制动力计算结果如图6所示,钢轨受压为正。计算梁轨相对位移时,桥墩纵向水平刚度值分别取200 kN/cm/线、150 kN/cm/线、100 kN/cm/线及50 kN/cm/线,计算结果见图7。

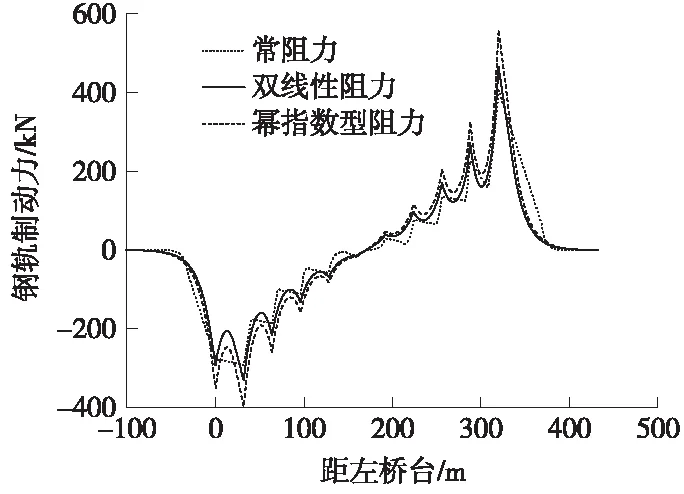
图6 钢轨附加制动力分布

图7 梁轨相对位移曲线

由计算结果可以看出,全桥范围内制动时,常阻力形式下最大制动力为52.39 MPa；双线性计算结果为60.08 MPa；幂指数型计算的最大制动力为72.05 MPa。桥墩纵向水平刚度取不同值时，梁轨最大相对位移值如表3所示。

表3 梁轨相对位移最大值 mm

由计算结果可知,3种线路阻力形式下的钢轨附加制动力分布规律相同,但大小不同,其中常阻力最小,幂指数型最大,双线性次之。桥墩纵向水平刚度取200 kN/cm/线时,常量阻力计算得到的梁轨相对位移为5.6 mm,约是幂指数型的3倍,双线性约为幂指数型的2倍,已超过我国规范要求的检算标准4 mm,这就需要增加桥墩纵向水平刚度或设置小阻力扣件,造成资源的不必要浪费。幂指数型阻力在线路位移较小时的阻力取值较双线性要大,在制动荷载作用下,可以将荷载很快地传至桥梁上,因此梁轨相对位移较双线性要小。由计算结果还可以看出,随着桥墩刚度的降低,3种阻力形式下梁轨相对位移越来越大,当桥墩刚度超过150 kN/cm/线时,均已超过检算标准。由线性插值求得当采用常量阻力计算得到的梁轨相对位移为4 mm时,桥墩最小刚度取值为280 kN/cm/线,双线性为190 kN/cm/线,幂指数型为130 kN/cm/线,由此可见,在制动工况下,通过梁轨相对位移来确定桥墩最小纵向水平刚度时,不同线路阻力形式下差异较大。

3.3 断轨力计算

计算钢轨断轨力时,钢轨降温幅度取50 ℃。计算钢轨断缝值时,为了分析线路阻力形式在不同降温幅度下对其影响,取30、40 ℃和50 ℃ 3种形式。钢轨断缝位于右桥台处,计算结果如图8、图9所示。

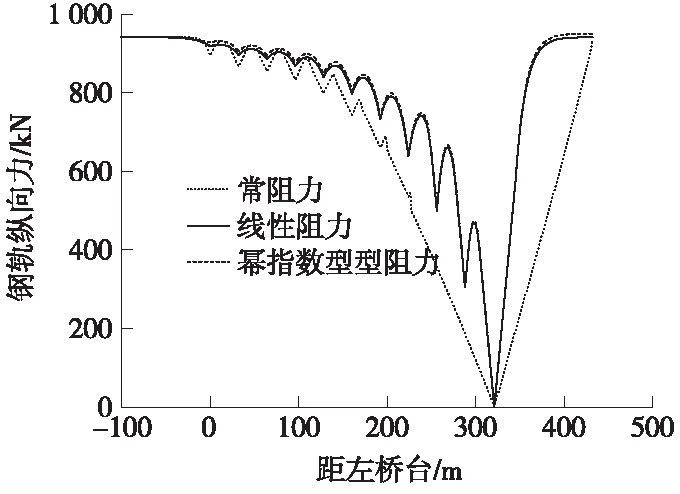
图8 钢轨降温50 ℃时断轨力

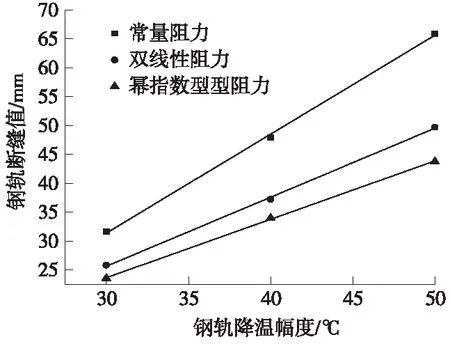
图9 钢轨断缝值比较曲线

由钢轨断轨力分布图知,左桥台处钢轨断轨力有最大值,且3种线路阻力形式下相差不大。断缝值计算结果见表4。

表4 钢轨断缝值 mm

由计算结果可知,双线性和幂指数型阻力计算得到的钢轨断缝值相差不大,但均小于常量阻力计算所得值,且随着钢轨降温幅度的增加差值变大。这主要是因为断缝附近钢轨温度力梯度基本上为线路极限阻力,双线性阻力及幂指数型在梁轨相对位移达到2 mm时的极限阻力大小基本相等,而常量阻力极限阻力是通过大量计算按测试值的0.5～0.8倍取值而得,有可能会导致在计算时结果偏大。