列车制动对刚构桥上无缝线路梁轨相对位移的影响研究

2013-01-17熊震威谢铠泽

铁道标准设计 2013年10期

熊震威,谢铠泽,刘浩,王平

(西南交通大学高速铁路线路工程教育部重点实验室,四川成都 610031)

桥上无缝线路设计时,为了保证道床的稳定性,UIC(International Union of Railways)标准中规定计算制动力时,梁轨相对位移不宜大于4 mm[1]。该限值对于指导铁路桥梁墩台纵向水平刚度的设计十分重要。虽然我国《新建铁路桥上无缝线路设计暂行规定》中并未对制动力检算进行规定,但是在无缝线路设计过程中，设计者已经参照UIC标准的规定将制动力考虑在内,从而规定了不同跨度简支梁桥的墩顶纵向水平线刚度最小值。

目前研究梁、轨位移时,只是单独考虑了简支梁桥桥墩刚度或刚构桥桥墩刚度对其的影响。对于简支梁桥而言,在线路纵向阻力等参数一定的情况下,一般只能通过增加主桥桥墩纵向水平线刚度，以减小制动力作用下的梁轨相对位移。由于刚构桥跨度比较大,刚构桥桥墩纵向水平线刚度也较大,如果继续提高桥墩刚度,就意味着工程量的增加,工程造价会大幅度提高。在某些特殊情况下,由于地形、选线等方面的特殊原因,增加主桥桥墩纵向水平刚度不仅十分困难而且代价非常高。综合考虑以上因素,在满足结构物安全的情况下,研究了刚构桥桥墩纵向水平刚度与其相邻跨的简支梁桥桥墩纵向水平刚度的合理匹配,最终选取合理的桥墩纵向水平刚度，从而降低工程造价。

1 计算模型与基本参数

1.1 模型建立

随着计算机及有限元方法的发展,桥上无缝线路若采用有限元方法求解,则其对应的模型有很多种,例如桁杆单元模型、桁式杆件加平面桥模型、抗弯杆件加刚臂桥模型、抗拉压桁式杆件加刚臂桥模型、单/双层弹簧阻力模型以及空间整体模型等。本文主要采用目前比较通用的单层弹簧阻力模型进行分析,如图1所示。在该模型中线路纵向阻力采用非线性弹簧模拟,梁采用平面单元及带刚臂的刚架来模拟[2],该模型可同时适用于伸缩力、挠曲力、断轨力、制动力的计算。其中图1(a)模型主要用于计算伸缩力、断轨力及制动力,图1(b)模型主要用于挠曲力的计算,由于本文主要研究制动荷载下的梁轨相对位移,因此主要采用图1(a)模型。

图1 单层弹簧阻力模型

1.2 基本假设

图1(a)是简化之后的计算模型,根据梁轨相互作用原理以及刚构桥的特点,做出以下计算假定：

(1)假设桥梁固定支座能完全阻止梁的伸缩,不考虑支座本身的纵向变形,固定支座承受的纵向力全部传递至墩台上,活动支座抵抗伸缩的阻力可忽略不计,计算时不考虑梁在支座外的悬出部分的伸缩量；

(2)不考虑桥梁护轨对无缝线路纵向力及位移计算的影响；

(3)有砟轨道桥上不考虑梁端头道砟断面所传递的纵向力,假设道床所承受的纵向阻力全部传递至桥梁墩台上；

(4)桥梁墩台顶纵向刚度假定为线性,包含在支座顶面纵向水平力作用下的墩身弯曲、基础倾斜、基础平移及橡胶支座剪切变形等引起的支座顶面位移,桥梁墩台及基础的竖向刚度即为桥梁支座竖向刚度；

(5)钢轨与桥梁、钢轨与路基间的纵向约束阻力均假定为纵向弹簧约束,其位移阻力特性与梁轨间、钢轨与线路间的纵向阻力一致。

1.3 刚构桥桥墩刚度

桥梁墩台纵向水平刚度为使桥梁墩台支承垫石顶产生单位纵向水平位移时所需的纵向作用力,如图2所示。

图2 墩台纵向水平刚度计算图示

(1)

式中，∑δi=δp+δφ+δh；H为作用在墩台支承垫石顶的纵向水平力；δp为在H作用下,由墩身弯曲引起的墩台支承垫石顶纵向水平位移；δφ为在H作用下,由基础倾斜引起的墩台支承垫石顶纵向水平位移；δh为在H作用下,由基础平移引起的墩台支承垫石顶纵向水平位移。

对于简支梁或连续梁桥桥墩纵向水平刚度可以采用图2进行计算,对于刚构桥,由于桥墩与梁体固结在一起,在横向力H作用下,墩身位移、基础倾斜等引起的墩身弯曲应该考虑桥梁梁体的影响,会使刚构桥桥墩的纵向水平线刚度增加；假设桥墩墩身等截面、不考虑基础位移,采用结构力学方法计算可知,考虑梁体对墩身弯曲影响时的桥墩刚度约为不考虑梁体截面影响的4倍。

1.4 主要计算参数

以5×32 m简支梁+(L1+L2+L3)连续刚构桥+5×32 m简支梁为例,桥跨及支座布置如图3所示。

图3 桥跨及支座布置

列车起动/制动时，作用于钢轨面的牵引/制动力的大小主要取决于轮轨黏着系数。由于轮轨黏着系数受到列车编组形式、制动方式、轴重、制动时的速度、轮轨表面状态和气候等因素的影响,各国对轮轨黏着系数的规定存在较大的差异。国内外轮轨黏着机理的理论分析和试验研究表明,随着速度的提高,轮轨黏着系数有下降的趋势；在中低速情况下,随着轴重的增加,轮轨黏着系数有所下降。铁道科学研究院在“八五”科技攻关研究中,对桥上无缝线路的计算模型和参数建议值研究,提出了轮轨黏着系数取为0.164,故本文在计算中取为0.164。列车荷载采用中-活载,制动荷载长度取为400 m(如果桥梁总长小于400 m,则取为桥梁总长)；线路纵向阻力依照《新建铁路桥上无缝线路设计暂行规定》取值

[3]

。

2 计算结果

2.1 制动力及位移分布规律

以L1=L3=80 m,L2=128 m为例,刚构桥左右各1跨简支梁固定支座墩顶纵向水平线刚度取为550 kN/(cm·双线),其他简支梁跨桥墩纵向水平线刚度为400 kN/(cm·双线),桥台纵向水平刚度取为3 000 kN/(cm·双线),刚构墩纵向水平线刚度取为1 100 kN/cm·双线,列车入桥方向为从右向左,制动力方向同列车入桥方向相同,荷载作用范围从刚构桥左边跨端向右400 m范围[4-6],计算得到钢轨制动力及钢轨位移、桥梁位移以及梁轨相对位移，结果见图4与图5。

图4 钢轨纵向力分布

图5 钢轨及桥梁纵向位移分布

由图4与图5可知,钢轨制动荷载作用下,带动钢轨及各跨桥梁发生向右的纵向位移,钢轨的纵向位移是连续变化的,但由于桥梁的截面积比钢轨大得多,因此在位移分布图中，桥梁的纵向位移表现为台阶状，即为每联梁的刚体移动,这样必然存在如图5中点线表示的梁轨相对位移曲线。由于梁轨位移差的存在,才使得钢轨受到的纵向力不仅仅是制动荷载而且还存在线路阻力荷载,这两种荷载的合力即为钢轨的纵向力,钢轨所受最大压力发生在制动荷载开始的位置即刚构桥左端位置,大小为400.6 kN,钢轨所受最大拉力发生在制动荷载末端对应的简支梁端部,大小为221.9 kN。

依据上述简支梁与刚构桥桥墩的纵向水平刚度值的匹配关系,计算得出梁轨相对位移最大值为3.57 mm,未超过规范规定的4 mm限值,证明这种刚度值的匹配关系是满足规范要求的。

2.2 简支梁与刚构桥桥墩刚度匹配关系对梁轨相对位移的影响

本节选取目前铁路上常用的3种跨度刚构桥梁为例,采用不同刚构桥桥墩刚度与简支梁桥墩刚度进行匹配(仅改变刚构桥相邻梁跨简支梁桥固定支座对应的桥墩刚度,其他简支梁桥墩刚度取为规范规定的最小值)，分析相应的梁轨相对位移最大值变化规律,从而依据制动荷载下梁轨相对位移限值，确定合理的刚度匹配值。在分析中简支梁桥墩纵向水平刚度取值范围为400～800 kN/(cm·双线)。这3种跨度的刚构桥桥跨分别为：(60+100+60) m、(80+128+80) m、(188+116+188) m,其中跨度为(188+116+188) m的刚构桥长度大于制动荷载长度400 m。

对于桥跨为(60+100+60) m的刚构桥,不同的桥墩刚度匹配值对应的梁轨相对位移最大值计算结果如图6与图7所示。

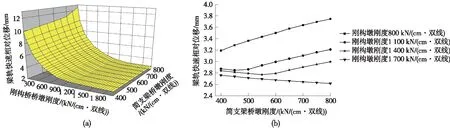
图6 刚度匹配对梁轨相对位移的影响

图7 纵向位移分布

由图6(a)整体结果可知,在简支梁桥墩纵向水平刚度不变时,梁轨相对位移随着刚构墩的纵向水平刚度的增加而逐渐减小,当刚构墩刚度大于500 kN/(cm·双线)时,随着墩的刚度增加,梁轨相对位移降低值并不大。其原因如图7所示,图中简支梁桥墩刚度均为400 kN/(cm·双线),刚构墩的刚度分别为500 kN/(cm·双线)与1 100 kN/(cm·双线),随着刚构墩刚度的增加,桥梁及钢轨的位移均减小并且降低值较大,两者差的绝对值虽然也在减小,但降低值较小,即梁轨相对位移变化不大；由图6(b)可知,梁轨相对位移并非随着简支梁桥墩刚度的增加而降低,而是当刚构墩刚度为1 100～1 400 kN/(cm·双线)时,梁轨相对位移随着简支梁桥墩刚度的增加先降低后增加,当刚构墩刚度小于1 100 kN/(cm·双线)时,梁轨相对位移随着简支梁桥墩刚度的增加而增加,当刚构墩刚度大于1 400 kN/(cm·双线)时,梁轨相对位移随着简支梁桥墩刚度的增加而降低。因此,就会存在刚构桥桥墩与简支梁桥墩纵向水平刚度合理匹配的问题,使梁轨相对位移尽可能的降低。

针对于该跨度的刚构桥桥梁,当刚构桥桥墩纵向水平刚度小于1 100 kN/(cm·双线)时,与刚构桥相邻的两跨简支梁固定支座对应的桥墩的刚度取值应该越小越好,这样不仅可以减小附加伸缩力以及降低制动荷载下的梁轨相对位移,而且可以降低工程量与费用；当刚构桥桥墩纵向水平刚度大于1 400 kN/(cm·双线)时,与刚构桥相邻的两跨简支梁固定支座对应的桥墩的刚度取值应该越大越好,但是考虑增大刚度会增加附加伸缩力以及工程造价,因此需要综合比较之后进行选择；当刚构桥桥墩刚度处于1 100～1 400 kN/(cm·双线)时,应该以附加伸缩力增加不大且梁轨相对位移降低较多为目标进行确定。以刚构桥桥墩刚度为1 100 kN/(cm·双线)时计算得到的附加伸缩力最大值与制动荷载下梁轨相对位移结果如表1所示。

表1 附加伸缩力最大值与梁轨相对位移

对原始数据采用归一化处理[7],假设这两个指标的重要程度相同,则将处理的数据绘制在以简支梁桥墩纵向水平刚度为横坐标的图中,2个曲线交点对应的刚度就是仅考虑这两种因素时,与刚构桥桥墩刚度匹配的最优刚度值,如图8所示。由图8可知,两线交点对应的刚度值约为455 kN/(cm·双线),即同时考虑桥梁伸缩时的钢轨附加伸缩力与列车制动时的梁轨相对位移,两者的重要程度相同时,简支梁桥墩台最优刚度为455 kN/(cm·双线)。

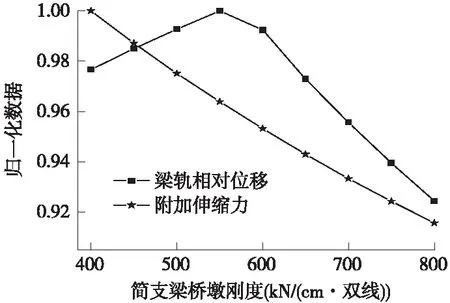
图8 归一化数据

对于桥跨为(80+128+80)m的刚构桥,也存在如上所述结论,只是刚度值达到2 600～3 000 kN/(cm·双线)时才出现上述现象。而桥跨为(188+116+188) m的刚构桥,在刚构桥刚度达到5 000 kN/(cm·双线)时仍未出现这种现象。因此,要出现梁轨相对位移随着简支梁桥墩刚度增加先降低后增加的现象,对应刚构桥桥墩刚度随桥梁总长的增加而增加,这两种桥跨的计算结果如图9与图10所示。

图9 (80+128+80) m刚构桥梁轨相对位移

图10 (188+116+188) m刚构桥梁轨相对位移

对于跨度为(80+128+80) m与(188+116+188) m的刚构桥梁,虽然也会出现同跨度为(60+100+60) m刚构桥相同的规律,但是该规律出现时对应的刚构桥桥墩刚度较大,而实际的桥墩刚度均不在该范围内,所以刚构桥相邻两跨简支梁桥固定支座对应的桥墩刚度应尽可能地取小值,以降低制动荷载作用下的梁轨相对位移及附加伸缩力值。

基于上述分析,不仅可以通过增加刚构桥桥墩纵向水平刚度的方法降低梁轨相对位移,还可以依据刚构桥的长度,选择合理的刚构桥与邻跨简支梁桥墩纵向水平刚度匹配关系,降低制动荷载作用下的梁轨相对位移。同时,当刚构桥桥墩刚度过大时,如果采用降低简支梁桥墩纵向水平刚度的方法,不仅可以降低梁轨相对位移,还可以降低附加伸缩力。

3 结论及建议

通过建立刚构桥上单层弹簧阻力计算模型,分析了刚构桥桥墩纵向水平线刚度与相邻两跨简支梁固定支座对应的桥墩纵向水平刚度的匹配关系,对制动荷载下的梁轨相对位移规律进行了计算分析,得到如下结论及建议。

(1)全桥制动时,刚构桥桥墩纵向水平刚度存在一个范围,在该范围内,梁轨相对位移随着刚构桥两端简支梁桥桥墩纵向水平刚度的增加先降低再增加；小于该范围时,梁轨相对位移随着简支梁桥桥墩刚度的增加而增加；而大于该范围时梁轨相对位移的变化规律与小于该范围时的规律相反；且该刚度范围随着刚构桥总长度的增加而增大。

(2)在简支梁桥桥墩纵向水平刚度不变时,刚构桥在制动荷载作用下,梁轨相对位移随着刚构墩纵向水平刚度的增加而降低。

(3)工程上可以通过增加刚构桥桥墩纵向水平刚度或选择合理的刚构桥与相邻跨简支梁桥桥墩纵向水平刚度匹配关系,达到降低梁轨相对位移的目的。同时,当刚构桥桥墩刚度过大时,如果采用降低简支梁桥桥墩纵向水平刚度的方法,不仅可以降低梁轨相对位移,还可以降低附加伸缩力。

(4)当附加伸缩力与降低梁轨相对位移的变化不一致时,可采用归一化的数据处理方法得到其最优刚度取值。对(60+100+60) m的刚构桥,当刚构桥桥墩刚度为1 100 kN/(cm·双线)时,采用上述方法可得简支梁桥的墩台最优刚度为455 kN/(cm·双线)。

[1] 广钟岩,高慧安.铁路无缝线路 [M].北京：中国铁道出版社,2012．

[2] 王新敏.ANSYS 工程结构数值分析[M].北京：人民交通出版社,2010．

[3] 中华人民共和国铁道部.铁建设函[2003]205号新建铁路桥上无缝线路设计暂行规定[S].北京：中国铁道出版社,2003．

[4] 魏贤奎,陈小平,王平.有砟轨道基础桥上无缝线路计算软件开发与应用[J].铁道建筑,2010(8)：115-118.

[5] 杨艳丽.铺设无缝线路的桥梁墩台纵向线刚度设计研究[D].长沙：中南大学,2008．

[6] 崔宏.轻轨高架桥连续梁墩顶纵向水平线刚度设计探讨[J].铁道标准设计,2011(7)：52-54.

[7] 黎国清,庄军生,张士臣.高速铁路桥上无缝线路附加力的研究[J].中国铁道科学,1997,18(3):15-22.

[8] 吴仁义,张亚爽,汪力,王平.改善桥上无缝线路梁轨相互作用方法的研究[J]. 中国铁路,2012(5):80-83.

[9] 唐乐,朱彬.无砟轨道桥上无缝线路纵向力研究[J].铁道标准设计,2006(S1):81-82．