桩基础支撑的周期性高架桥结构的缺陷态研究

陆建飞,雷 力

(江苏大学土木工程系,江苏镇江 202013)

高速铁路是一个地区乃至整个国家的生命工程线。高速铁路对地基沉降有严格的要求,而高架桥恰能有效解决软土地基不均匀沉降的问题,因此,高架桥结构在高速铁路建设中得到了广泛应用。例如,京沪高速铁路中多数路段均采用高架桥结构[1]。为便于施工,高架铁路的常规路段常设计成由相同的桥跨构成,因此,上述高架铁路可简化为周期性结构。然而,由于地理环境等因素的影响,在工程实际中也常使得高架桥结构的某一跨或相邻几跨在材料或几何参数与标准跨不一致。根据周期性理论,上述与标准跨不一致的跨为高架桥结构的一种缺陷。在本文中,将不同于标准跨的跨定义为缺陷跨,称包含缺陷跨的周期性高架桥为缺陷周期性高架桥。

波在周期性结构中传播可追溯到1883年Floquet对一维Mathieus’s方程的研究。Mead、Lin等人对波在周期性梁类结构中传播的研究表明,规则的周期性结构具有“通频”和“禁频”特性[2-5]。通常缺陷能改变周期性结构的波动特性,因此,波在含缺陷周期性结构中传播比在标准周期性结构中传播更为复杂。例如,Sigalas[6]的研究表明缺陷使得周期性结构产生了额外的能带,且其波动局域在缺陷处。吴福根[7]对二维周期性结构的研究表明,当频率为缺陷频率时,缺陷态压强在结构的缺陷处呈现出极大值。后来,Khelif[8]从理论和实验上研究了周期性结构的缺陷态特性,均得到与上述理论相吻合的结果。

虽然目前存在一些关于周期性结构缺陷态的文献[5-8],但现存的研究均局限于周期性连续梁结构,对简支梁型的周期性结构缺乏研究。正如工程实际中的高架桥由单独梁组成,并通过桥墩和桩基础支撑,因而把高架桥结构简化为连续梁是不合理的。再者,由于目前尚未建立缺陷周期性梁类结构的超原胞方法,故对其超原胞的缺陷态也缺少研究。

本文主要目的是建立一个数值计算模型,求解简支梁型周期性高架桥结构缺陷态。本文的主体框架如下所述：为获得桩基础的柔度,首先利用边界元方法处理桩-土相互作用问题；然后,利用所得桩基础的柔度,梁和墩的传递矩阵及梁-梁-墩接头的联结条件,推导高架桥单跨的传递矩阵。基于超原胞的思想,建立了求解高架桥结构缺陷态的超原胞方法。最后,文中给出了桩基础支撑的周期性高架桥结构的缺陷态。

1 桩-土相互作用的边界元模型

在工程实际中,高架桥的每跨包含一个或多个桥墩,而每个桥墩由群桩基础支撑。为了简化,假设高架桥的每跨只包含一个桥墩,且高架桥的桩基础由单桩组成,高架桥的桩与桥墩之间为刚性联结,高架桥每跨中的梁与梁及梁与桥墩之间均通过弹簧连接。基于上述假设,周期性高架桥的每跨可简化为由单根桩基础,1个桥墩,左、右横梁及3根联结弹簧所组成的单元(图1)。另外,本节将建立桩-土耦合边界元模型处理桩-土相互作用问题。

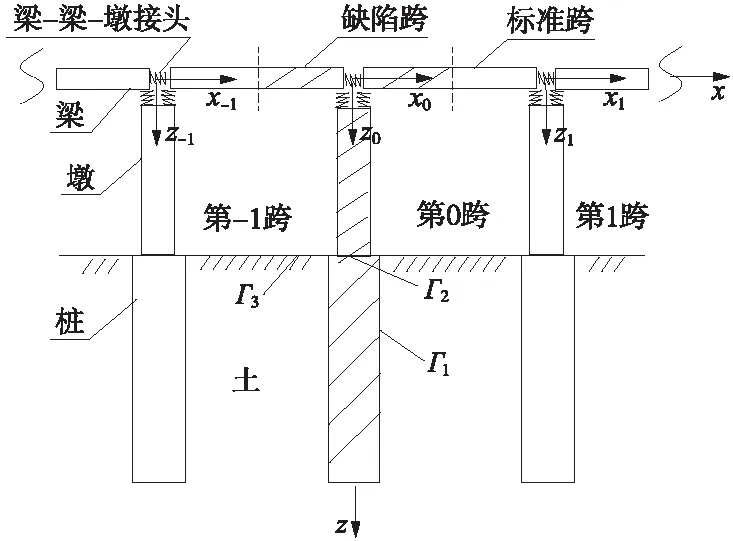
图1 含缺陷周期性高架桥结构示意

1.1 弹性介质的边界积分方程

在本文中,把桩和土体均处理成弹性介质。弹性介质在频域内的运动方程为[9]

μui,jj+(λ+μ)uj,ji=-ρω2ui(1)

式中,λ和μ为弹性介质的拉梅常数；ui和ρ分别为弹性介质的位移和密度；ω为角频率。另外,弹性介质的本构关系为[9]

σij=2μεij+λδije(2)

式中,σij和εij分别为弹性介质的应力和应变分量；e和δij分别为体积应变和内罗内克符号。基于动力互易定理, 弹性介质在频域内的边界积分方程为[10]

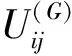
1.2 桩-土耦合边界元模型

在本节中,依据弹性介质的边界积分方程推导了桩和土体的边界元公式,并基于上述公式建立了桩-土耦合边界元模型。在如图1所示的桩-土耦合系统中存在3种边界面：桩和土体相交的界面为边界面Γ1；桩顶部为边界面Γ2；土体表面为边界面Γ3。

利用桩的边界积分方程,可得桩的边界元公式为

H(p)u(p)=G(p)t(p)(4)

式中,上标p代表桩；u(p)和t(p)分别为桩边界面上单元节点的位移向量和面力向量；G(p)和H(p)代表系数矩阵。公式(4)可重新推导为

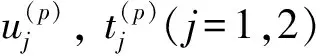
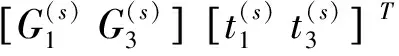
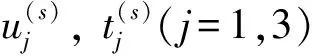
在桩和土体的边界面Γ1和Γ3上,有如下连续性和边界条件成立

(7)

基于公式(5)到(7),可得桩-土耦合边界元模型为

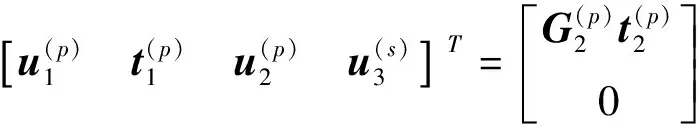
高架桥结构发生面外振动时,桩顶部有扭矩,剪力和弯矩作用。设高架桥第n号桩顶部的位移向量和力向量可分别表示为

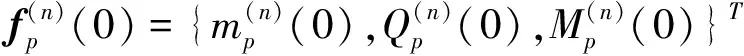
(10)

式中,Cp为桩基础的柔度矩阵。

2 周期性高架桥单跨的传递矩阵

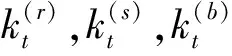
为便于描述高架桥第n跨的响应,在第n跨上建立如图1所示的局部坐标系。由于本文只考虑高架桥结构的面外振动,这里的梁和墩将产生扭转及面外弯曲振动,因此,梁和墩的传递矩阵可利用杆件的扭转振动和Bernoulli-Euler梁的弯曲振动理论推导。高架桥第n跨中的梁在扭转和面外弯曲振动下的控制方程分别为[11]

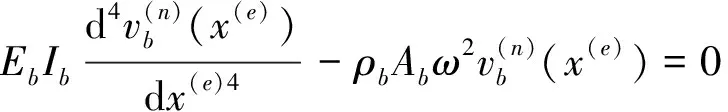
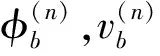
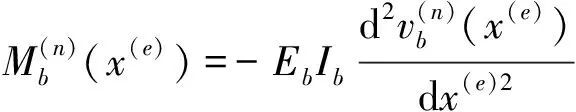
高架桥第n跨任意梁截面的状态向量可表示为

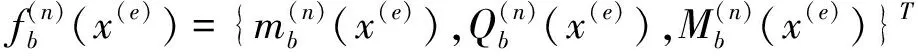
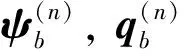
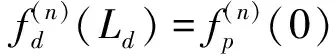
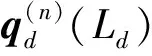
(15)

式中,Ld为桥墩的高度。

忽略3根联结弹簧质量,并利用公式(13)到(15)、梁-梁-墩接头处的平衡条件、弹簧的本构关系及墩的传递矩阵,可得高架桥第n跨梁-梁-墩(BBP)接头的左、右两端梁截面的状态向量所满足的关系式为

(16)

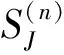
利用梁和BBP接头的传递矩阵及传递矩阵方法[13],可得高架桥第n跨左、右两端梁截面的状态向量所满足的关系式为

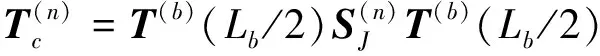
3 含缺陷周期性高架桥的超原胞方法及缺陷态

由连续介质组成的声子晶体中的缺陷会使其产生缺陷态[5-8],这里的周期性高架桥结构可认为是一种声子晶体结构。值得指出的是,目前尚未有文献研究简支梁型周期性结构的缺陷态。因此,本文基于超原胞的思想,建立缺陷高架桥结构的超原胞方法,求解周期性梁类结构的缺陷态。

为实施缺陷高架桥结构的超原胞方法,首先须选定含缺陷跨的超原胞,且超原胞包含的跨数必须使得缺陷态模态所对应的响应在超原胞的端部趋于零。设含缺陷周期高架桥的超原胞由2n+1跨组成,且中间跨为缺陷跨(第0跨),利用高架桥标准跨及缺陷跨的传递矩阵,可得超原胞两端的状态向量所满足的关系式为

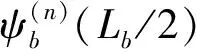
基于Bloch定理[14]和公式,可得高架桥超原胞的特征方程为

(19)

式中,LS=2nLb+L0为超原胞的长度；L0为缺陷跨的长度；κ为高架桥超原胞中的特征波波数。

4 数值结果和分析

基于公式(19),可得含缺陷周期性高架桥超原胞的缺陷态。在算例中,将考虑缺陷跨的梁和桥墩存在缺陷对高架桥的影响。假设桩和桥墩的横截面均为圆形,梁的横截面为矩形。对于标准跨,各参数的取值如表1所示。对于缺陷跨,与标准跨不一致参数的取值如下所示：桥墩的半径为0.5 m；右梁横截面高、宽分别为0.6 m和2.0 m,右梁的杨氏模量为2.2×1010Pa。

表1 桩、土、桥墩、梁和弹簧刚度等参数取值

注：BBP接头把梁为左、右梁

如图1所示的周期性高架桥在面外振动下存在3种特征波,由于第一、二种特征波是衰减波,因此,本文仅给出第三种特征波的结果。图2为高架桥超原胞中第三种特征波的能带。从图2(b)可知,频率5.0 Hz位于标准超原胞(15跨均为标准跨)的禁带内,但其又位于缺陷超原胞(由15跨组成,且中间一跨为缺陷跨)的通带内,这表明频率5.0 Hz为缺陷高架桥超原胞的缺陷态频率。显然,这个附加的通带频率由高架桥结构中含缺陷跨所引起。对于标准和缺陷超原胞,图2(b)还显示第三种特征波的虚部在高频范围内均很大。

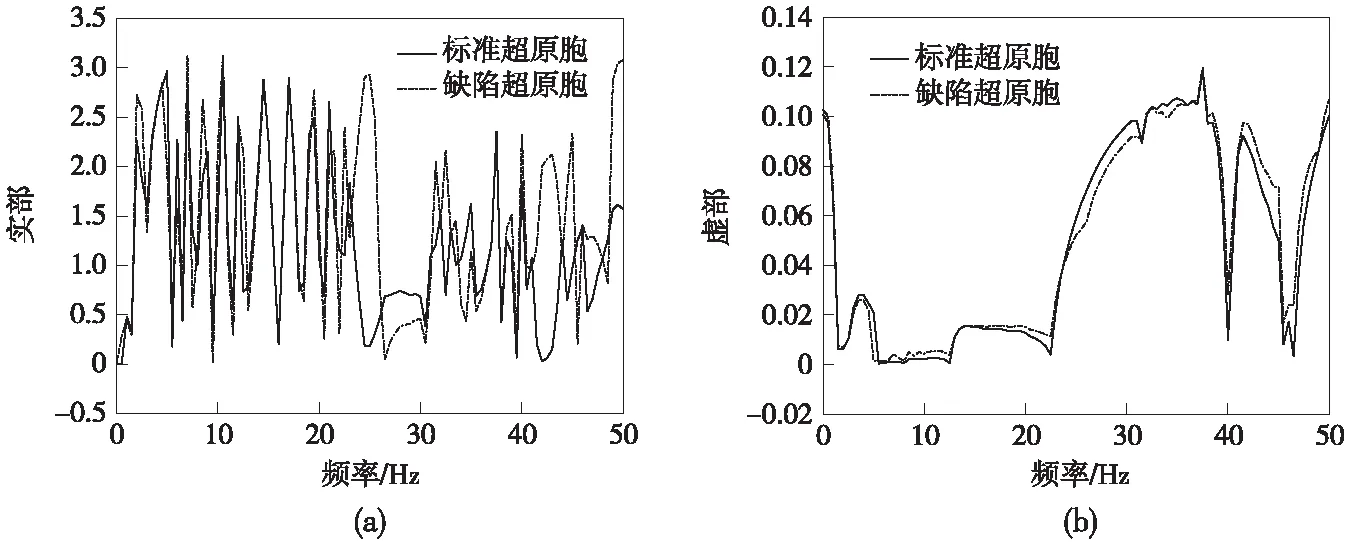
图2 超原胞中第三种特征波的能带

图3给出了超原胞内各跨梁左端和墩底在缺陷频率处的模态。图3(a)显示扭转角在缺陷跨两端的响应明显大于超原胞的其他跨,且远离缺陷跨的响应很小。对于超原胞内各跨墩底的扭转角,上述现象表现更为明显(图3(b))。此外,缺陷超原胞的模态还表明：波动局域在缺陷跨附近,并通过缺陷跨放大,类似于固体力学中的应力集中现象。

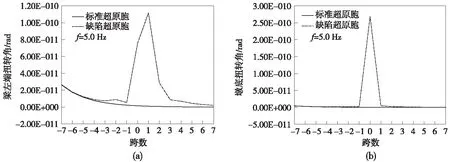
图3 超原胞在缺陷频率5.0 Hz处的模态

5 结论

本文建立了简支梁型周期性高架桥结构缺陷态计算模型,建立了计算高架桥结构缺陷态的超原胞方法。在模型中,引入联结弹簧把高架桥的梁-梁-墩接头处理成弹性接头。本文的计算结果表明，缺陷会使周期性高架桥结构产生额外的能带,即缺陷态；当频率为缺陷态频率时,超原胞的缺陷态模态在高架桥的缺陷跨处产生了显著的应力集中现象,显然,这对周期性高架桥结构的受力是极为不利的。本文所建立的模型可应用于求解高架桥支撑在层状地基上的缺陷态,还可推广用于处理高架桥结构含多个相邻缺陷跨的情形。

附录A：公式(16)的表达式

公式(16)中矩阵A和B的表达式为

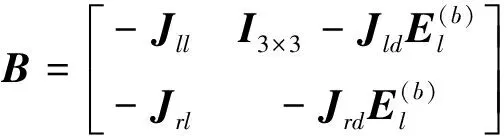
式中,

其中,Cd为桥墩的柔度矩阵,即

(A.2)

[1] 孙树礼.京沪高速铁路桥梁工程[J].铁道标准设计,2008(6)：1-4．

[2] Mead D J. Free wave propagation in periodically supported infinite beams[J]. Journal of Sound and Vibration, 1970,11(2):181-197．

[3] Mead D J, Markus S. Coupled flexural longitudinal wave motion in a periodic beam [J]. Journal of Sound and Vibration, 1983,90(1):1-24．

[4] Lin Y K. Free vibrations of a continuous beam on elastic supports [J]. International Journal of Mechanical Sciences, 1962,4(5):409-423．

[5] 温熙森,等.声子晶体[M].北京：国防工业出版社,2009．

[6] Sigalas M M. Elastic wave band gaps and defect states in two-dimensional composites[J]. Journal of Acoustical Society of America, 1997,101(3):1256-1261.

[7] 吴福根,刘有延.二维周期性复合介质中声波带隙结构及其缺陷态[J].物理学报,2002,51(7)：1434-1438．

[8] Khelif A, et al. Trapping and guiding of acoustic waves by defect modes in a full-band-gap ultrasonic crystal[J]. Physical Review B, 2003,68(1):214301．

[9] Achenbach J D. Wave Propagation in Elastic Solids[M]. Amsterdam: North-Holland, 1973．

[10] Banerjee P K, Butterfield R. Boundary Element Methods in Engineering Science[M]. UK: McGraw-Hill, 1981．

[11] Graff K F. Wave Motion in Elastic Solids[M]. Oxdord: Clarendon Press, 1975．

[12] Lu J F, Jeng D S. Energy bands of a periodic viaduct in out-of-plane vibration: Coupling with a half-space[J]. Europuean Journal of Mechanics-A/Solids, 2012,31(1):21-36．

[13] Dowling J P. Sonic Band structure in fluids with periodic density variations[J]. Journal of the Acoustical Society of America, 1992,91(5):2539-2543．

[14] 阎守胜.固体物理基础[M].北京：北京大学出版社,2011．