脉冲等离子体推力器特氟隆烧蚀过程数值模拟①

谢泽华，周 进

(国防科技大学高超声速冲压发动机技术重点实验室，长沙 410073)

0 引言

脉冲等离子体推力器(Pulsed Plasma Thruster，PPT)具有结构简单、易于集成、控制方便、响应快速、能产生小而精确的推力脉冲、所需星上电源功率小等优点，可广泛用于微小卫星的姿态控制和轨道保持等任务，是微小卫星推进技术研究的热点和重要方向之一［1］。PPT利用脉冲放电烧蚀或加热推进剂，并使其电离形成等离子体，等离子体在电磁力和气动压力作用下加速喷出推力器，产生脉冲推力。根据所使用的推进剂，PPT有多种不同类型，其中最常见的是使用固体聚四氟乙烯(俗称特氟隆)的烧蚀型脉冲等离子体推力器。在数十年的研究与应用过程中，PPT一直面临着效率较低的问题［2］。作为推力器工作的重要阶段，推进剂烧蚀对推力效率具有直接重大的影响。为了掌握PPT的工作机理，提升推力效率，有必要对推进剂烧蚀过程开展细致深入的研究。目前，已经发展了一些模型用于PPT中特氟隆推进剂的烧蚀计算。Brito等［3］提出了一个零维模型，将烧蚀质量表达为放电参数和推力器几何参数的函数，适用于推力器的性能预估。Turchi等［4］在一维准稳态高磁雷诺数高磁压等离子体流动假设下，得到了用放电电流表示的烧蚀质量流率的表达式，可用于PPT工作过程的一维简单分析。Thomas［5］和 Henrikson［6］在对 PPT 的研究过程中，采用过相似的简化烧蚀模型，将烧蚀质量流率表示为热流密度与特氟隆的蒸发潜热之商，这一模型并不能得到推进剂温度分布的信息，适合于只关心推力器总体性能和等离子体流动过程的研究场合。Mikellides［7］将特氟隆烧蚀视为一个物质升华的过程，假设在特氟隆表面存在一层饱和蒸气，表面压力由平衡蒸气压曲线计算，表面温度根据热传导方程计算，烧蚀质量流率根据等离子体流动的动量方程由流动入口处的压力梯度确定，Lin［8］和 Antonsen［9］则在各自研究中，利用平衡蒸气压曲线直接将烧蚀质量流率表示为特氟隆表面温度的函数。同样利用平衡蒸气压曲线，Keidar和Boyd［10］建立了一个动理学模型，假设推进剂表面存在一个动理学非平衡层和一个流体力学非平衡层，推进剂烧蚀质量流率根据推进剂表面温度和等离子体密度、温度计算。这些模型被应用到PPT的数值研究中，并取得了大量的研究成果。然而，由于它们并没有反映出特氟隆烧蚀的具体过程，当前研究者们对PPT中推进剂烧蚀特性的认识还较有限。在将特氟隆用作热防护材料的研究过程中，Clark［11］提出了第一个较为全面考虑真实物理化学过程的一维两相烧蚀模型，将特氟隆划分为晶体和无定形体两种状态。Holzknecht［12］建立了一个相似模型，考虑了热膨胀效应和高分子化合物的生成，模型计算复杂，但与Clark的实验结果吻合很好。Arai［13］简化了烧蚀过程，在 Clark模型的基础上，考虑了特氟隆对辐射的吸收和透射的影响，证明了两相假设对精确预测特氟隆温度分布和热传递属性有着关键作用。Clark、Holzknecht和Arai对特氟隆烧蚀防护做了大量具有重要意义的研究工作，他们建立的模型代表着目前对特氟隆烧蚀过程最详细的分析。PPT的工作过程呈现出明显的多维特性，而且推进剂烧蚀过程与等离子体流动传热过程联系紧密相互影响。

为深入探究PPT的工作特点和性能规律，本文以Clark等人的工作为基础，建立了特氟隆的二维两相烧蚀模型，在与等离子体流动传热过程耦合计算的情况下，考察了PPT中特氟隆的烧蚀过程及对推力效率的影响。

1 计算模型

1．1 烧蚀传热方程

在低于600 K的温度下，特氟隆是白色晶状长链聚合物，温度达到600 K时发生相变，成为具有极高粘性的无定形体，同时高聚物分子开始解聚、分解，生成单体小分子产物［13］。特氟隆烧蚀过程如图1所示，在晶体和无定形体两个区域分别考虑传热过程，给出导热微分方程如下:

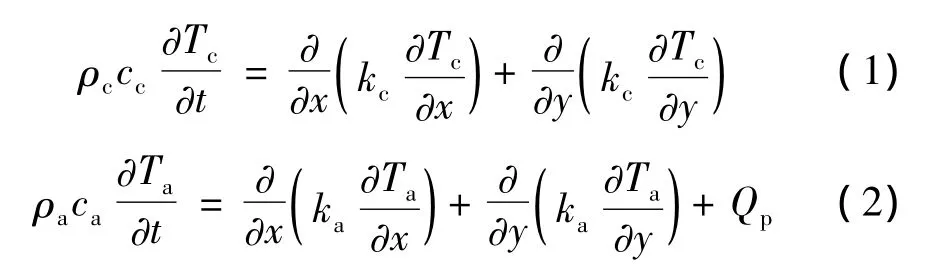
其中，ρ、T、k分别表示特氟隆的密度、温度和导热系数;下标c表示晶体;下标a表示无定形体;Qp表示单位体积的特氟隆分解产生的热量，用Arrhenius反应定律表示为

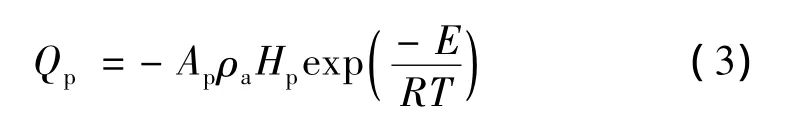
式中 Ap为频率因子;Hp为热解热;E为活化能。

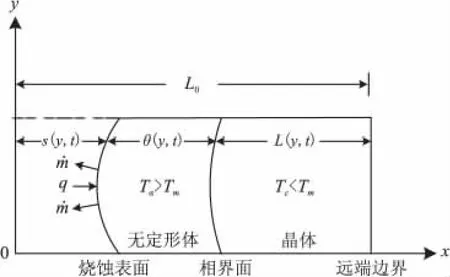
图1 烧蚀过程示意图Fig．1 diagram of the ablation process

1．2 烧蚀传热边界条件

在烧蚀表面上，净传入的热流密度由外部传入热流密度、表面辐射损失及烧蚀质量带走的能量确定，边界条件可表示为

其中，下标s表示烧蚀表面;δ为当地表面切线方向与y轴的夹角;hs为烧蚀产物的比焓。

推进剂烧蚀发生在烧蚀表面附近非常薄的微米量级厚度的区域内，烧蚀表面的后退速度和烧蚀质量通量可根据特氟隆分解速率由下式计算:

式中 ρ0为特氟隆的参考密度;s和θ分别为烧蚀表面的后退距离和无定形体区域的长度。

在相界面上，推进剂的温度等于相变温度Tm。相界面的运动速度可根据热流平衡条件求出，对其积分可计算出相界面的位置。

式中 ρm为相界面处的平均密度;hm为相变潜热。

其余表面采用绝热边界条件。

1．3 等离子体流动与传热

大量的计算结果表明［7］，热传导是PPT中等离子体向推进剂传递热量的主要方式。因此，忽略对流和辐射传热，假设传给推进剂表面的热流密度由表面附近的重粒子和电子的导热系数及等离子体的温度梯度确定。

等离子体的流动与传热属性采用磁流体力学方法进行描述，控制方程组为

式中 ρ为密度;U为速度;B为磁场强度;p为压强;et为总比能;νe为磁扩散率;τ=为粘性应力张量;q为热流密度矢量;μ0为真空磁导率。

2 数值方法

2．1 坐标变换

推进剂烧蚀过程中，烧蚀表面和相界面的位置是随时间变化的。为计算方便，作如下坐标变换:

经过变换后，新的坐标χ在无定形体区域的取值范围和ξ在晶体区域的取值范围均为［1，0］。在新的坐标系(χ，y)中，烧蚀传热方程(2)变换后的形式为

其中

烧蚀传热方程(1)在坐标系(ξ，y)中具有与式(10)相似的形式。此外，原坐标系中的边界条件也需进行坐标变换，这里对变换结果予以省略。

2．2 离散求解

本文采用有限差分方法，对烧蚀传热方程进行求解。在特氟隆烧蚀过程中，无定形体区域的厚度非常小，为避免显示格式计算时因稳定性限制带来的计算时间难以承受的问题，这里采用隐式格式进行计算。

在均匀网格上对时间导数项采用一阶前向差分，空间导数项采用二阶中心差分，对内热源项进行泰勒级数展开，变换后的控制方程可离散成如下九点形式:

式中 a1，a2，…，a10为系数。

直接求解式(12)，需对一个大型稀疏矩阵作矩阵运算，难度很大。本文采用加权-对称超松弛迭代算法(WSSOR)进行求解。对磁流体力学方程组引入双曲型散度清除方法，以避免伪磁场散度对数值求解的影响，对无粘通量采用M-AUSMPW+格式进行差分，对粘性项采用中心差分，整个控制方程组采用基于隐式LU-SGS格式的双时间步方法进行求解。

3 验证算例

3．1 导热过程

考虑单相物体内的一维非稳态导热问题。假设物性参数恒定，初始温度为T0，当热流密度q保持恒定时物体的温度分布存在解析解［14］:

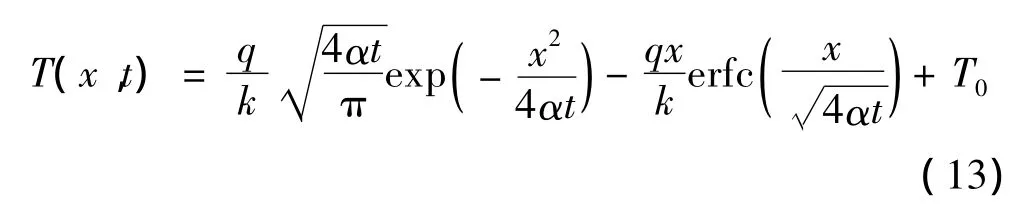
式中 α为热扩散率。

采用二维程序进行一维计算，计算结果见图2。图2中，3个时刻的数值解与解析解的温度分布曲线均高度重合，表明程序能对非稳态热传导过程进行准确模拟。

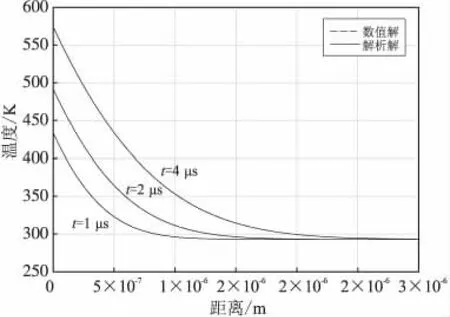
图2 导热过程中的温度分布Fig．2 Temperature distribution in the heat conduction process

3．2 相变过程

考虑相界面运动和相变潜热对温度分布的影响。假设特氟隆在初始时刻处于晶状固相，初始温度为相变温度，t＞0时在其前端表面施加一个热流密度保持为q的外部热源，不考虑特氟隆的分解吸热，假设相变后的区域内温度分布是坐标的二次方函数，则在物性参数保持恒定的条件下，可得到温度分布近似解［14］:

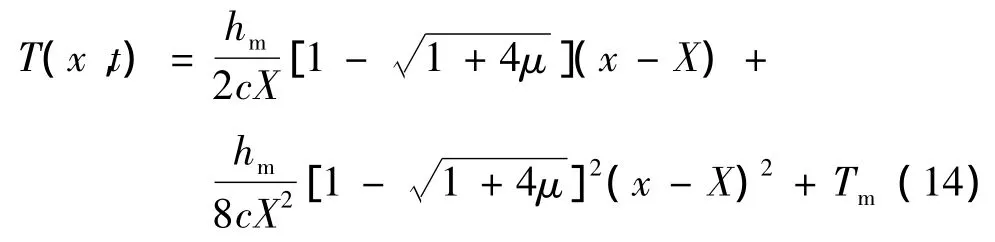
其中，系数μ和相界面的位置X由式(15)计算:

图3给出了考虑相变过程的温度分布曲线，图3中的数值解和近似解较接近，说明程序能较好地对特氟隆的相变过程进行模拟。

图3 相变过程中的温度分布Fig．3 Temperature distribution in the phase transition process

3．3 烧蚀过程

假设烧蚀表面附近的温度呈线性分布，特氟隆密度保持恒定，Kemp［15］给出了稳态烧蚀情况下，由烧蚀表面温度Ts确定烧蚀质量通量和烧蚀表面后退速度的近似计算公式:

式中 Bp为活化温度;hs－h－∞表示推进剂烧蚀前后的焓差。

利用编写的程序计算特氟隆在恒定热流密度作用下烧蚀过程达到稳定状态时的烧蚀特征参数，将计算结果与据式(16)、式(17)得到的近似值进行比较，结果见图4。图4中的数值解与近似解符合较好，表明程序能较准确地计算出特氟隆的烧蚀特性。

图4 稳态烧蚀质量通量和烧蚀表面后退速度Fig．4 Steady-state ablated mass flux and surface recession velocity

4 计算结果及分析

4．1 计算条件

本文对常见的平行板电极PPT的典型工况进行模拟，PPT的结构参数及电参数见表1。

表1 PPT结构参数及电参数Table 1 Configuration and electric parameters of PPT

数值模拟的计算区域分为2部分，即特氟隆烧蚀传热区A和由放电通道B1及推力器出口下游延伸区B2组成的等离子体流动传热区，如图5所示。A区特氟隆传热距离L0取为20 μm，B1区的等离子体流动入口参数由烧蚀过程和放电电流确定，电极表面处理为等温滑移理想导体边界，延伸区B2是自由流动空间。

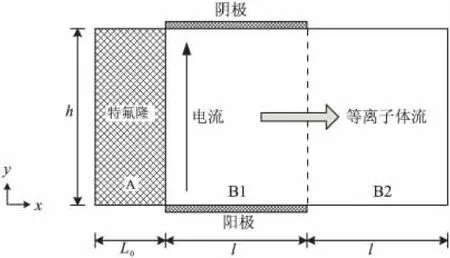
图5 计算区域Fig．5 Computational region

烧蚀过程数值模拟中，特氟隆的密度、比热容和导热系数都取为温度的函数，初始温度取为300 K，计算所需的物性参数取自Clark的文献［11］。

4．2 结果分析

PPT的放电过程可等效为一个RLC电路放电过程，在放电产生的强脉冲电流作用下，推进剂被加热分解，产生烧蚀。推进剂表面温度关于推进剂中心位置近似呈对称分布，图6为推力器的放电电流波形和y方向上距离电极0．05、0．10、0．20、0．50 倍电极间距处的表面温度变化曲线。放电开始时，放电电流急速增大，推进剂表面被迅速加热到分解温度以上。在放电电流达到脉冲峰值时，推进剂表面温度在高热流密度作用下继续升高，在放电电流达到峰值后约0．5 μs时，推进剂表面温度达到最大值。之后，随着电流振荡衰减而缓慢震荡回落。PPT工作时电极附近的电流密度最大，放电对等离子体的欧姆加热作用最强，传导到推进剂表面的热流密度也就最大，这使得靠近电极位置的推进剂表面温度明显高于其余位置，这也意味着这个位置的推进剂烧蚀速率更大，与实验结果相吻合。此外，由于电极附近等离子体中的电流密度相对更接近于放电回路中的电流密度，靠近电极位置的推进剂表面温度变化具有更明显的放电电流波动跟随性。

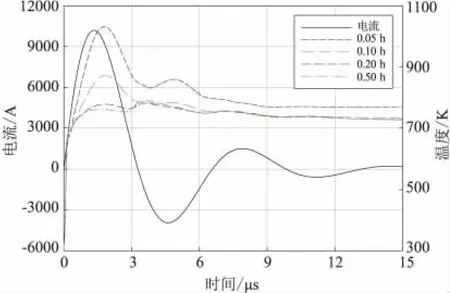
图6 放电电流和特氟隆表面温度Fig．6 Current waveform and surface temperature

图7给出了特氟隆烧蚀速率和烧蚀质量随时间的变化关系，对比图6可看出，在PPT放电的前1/4个振荡周期内，放电电流从0增大到最大值，而烧蚀速率和烧蚀质量却不大。在PPT放电的第二个1/4振荡周期内，推进剂烧蚀速率在放电电流达到峰值后，约0．5 μs时达到最大值，与此时的推进剂表面温度达到最高相对应。在这个1/4振荡周期内烧蚀的推进剂质量快速增加，占总烧蚀质量的比重超过95%。之后，随着推进剂表面温度下降，烧蚀速率迅速减小，烧蚀质量增加相当缓慢。

作为一种电磁推力器，PPT产生推力主要依靠等离子体受到的洛伦兹力J×B的加速作用，大的放电电流意味着高电流密度和强感应磁场，也就对应着大的加速力。PPT中推进剂烧蚀速率峰值时刻滞后于放电电流峰值时刻，大部分的烧蚀质量产生于放电电流达到最大值后不断减小的时间段内，这既不利于推进剂烧蚀产物的电离，也不利于等离子体的加速。这种推进剂烧蚀过程和推力器放电过程之间的匹配失衡，会极大地降低推进剂的使用效率和推力器的能量利用效率，导致推力效率低下。

图8给出了电极附近的推进剂在多个时刻点时的内部温度分布，图9为推进剂烧蚀过程中无定形体区域特氟隆的体积随时间的变化关系。

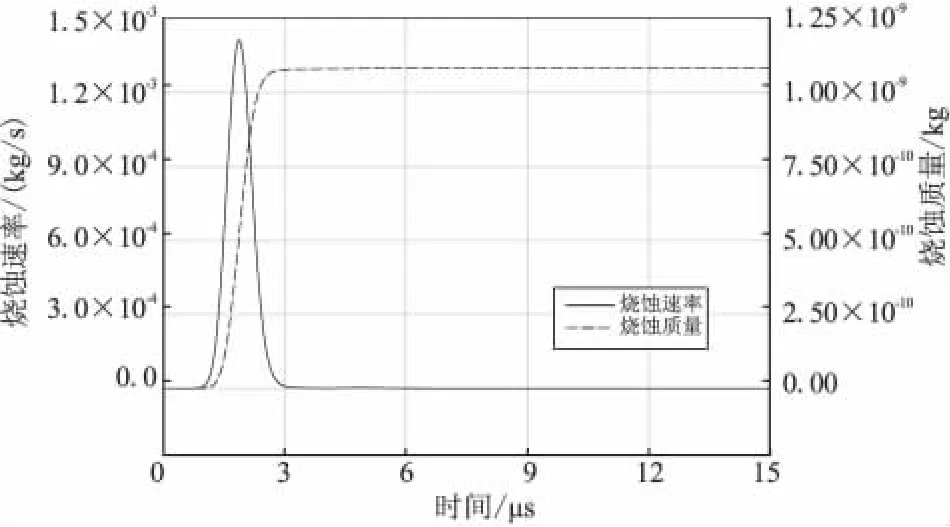
图7 特氟隆烧蚀速率和烧蚀质量Fig．7 Ablation rate and mass of Teflon

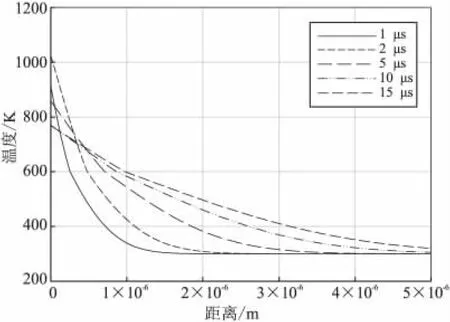
图8 y=0．05 h处的Teflon内部温度分布Fig．8 Temperature distribution in Teflon at y=0．05 h

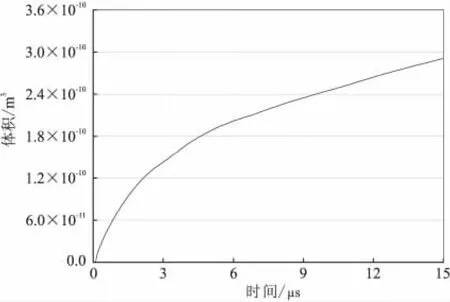
图9 无定形体特氟隆体积Fig．9 Volume of Teflon at amorphous phase

在放电开始的最初几微秒内，推进剂表面温度迅速上升，随着大量推进剂相变之后开始分解，烧蚀质量迅速增加。在PPT放电半个振荡周期之后，尽管有热量持续不断地传递给推进剂，使得发生相变的推进剂不断增多，推进剂远端温度不断升高，但由于热流密度减小，推进剂表面温度逐渐降低，推进剂烧蚀速率迅速下降到极低的水平，使得这一部分传入能量并没有被有效利用。此外，放电电流反向以后的电磁加速作用有所减弱，甚至计算发现部分区域的洛伦兹力会使等离子体运动减速，导致前期烧蚀产物长时间滞留于放电通道内。可见，PPT放电后期的能量利用效率较低，减小电流振荡，有助于提高推力效率。

Spanjers等［16］在实验中观察到在PPT放电结束后有大量特征尺度在1～100 μm范围的特氟隆微粒以低速喷出，这种粒子发射现象损耗了大量推进剂，由此产生的推力却可忽略。粒子发射现象的产生原因可能是由于推进剂表面附近具有很大的温度梯度及超过特氟隆相变温度的高温，使得处于表面附近的推进剂在因相变分解导致结构强度降低的情况下受热应力和表面之后的推进剂受热分解产生气体的挤压作用而被撕裂和冲刷带走。Spanjers等人是在放电开始100 μs后拍摄到粒子发射图像的，而在放电的前10 μs并没有找到这一现象存在的证据，在图9中成为无定形体的特氟隆体积在放电过程中不断增大，这意味着随后可能会有不少推进剂因粒子发射而被耗费掉。发生相变的推进剂体积由热流密度决定，在放电后期迅速关断放电电流和对推进剂进行冷却，可减缓无定形体特氟隆的体积增长，甚至使部分无定形体特氟隆再结晶成为晶状相。因此，这有助于减小因粒子发射带来的推进剂损失，从而提高推力效率。

5 结论

(1)靠近电极位置的推进剂表面温度更高，烧蚀速率更大。

(2)推进剂烧蚀速率峰值时刻滞后于放电电流峰值时刻，大部分的烧蚀质量产生于PPT放电的第2个1/4振荡周期内，烧蚀过程和放电过程之间的匹配失衡降低了推力效率。

(3)PPT放电后期的能量利用效率较低，减小电流振荡，有助于提高推力效率。

(4)在放电后期，迅速关断放电电流和对推进剂进行冷却，有助于减小因粒子发射带来的推进剂损失，从而提高推力效率。

［1］ Burton R L．Pulsed plasma thruster［J］．Journal of Propulsion and Power，1998，14(5)．

［2］ Spanjers G G，Mcfall K A，Gulczinski III F S，et al．Investigation of propellant inefficiencies in a pulsed plasma thruster［R］．AIAA 96-2723．

［3］ Brito C M，Elaskar S A，Brito H H，et al．Zero-dimensional model for preliminary design of ablative pulsed plasma Teflon thrusters［J］．Journal of Propulsion and Power，2004，20(6)．

［4］ Turchi P J，Mikellides I G，Mikellides P G，et al．Optimization of pulsed plasma thrusters for microsatellite propulsion［R］．AIAA 99-2301．

［5］ Thomas H D．Numerical simulation of pulsed plasma thrusters［D］．The University of Tennessee，2000．

［6］ Henrikson E M．An experimental and theoretical study towards performance improvements of the ablation fed pulsed plasma thruster［D］．Arizona State University，2010．

［7］ Mikellides Y G．Theoretical modeling and optimization of ablation-fed pulsed plasma thrusters［D］．Ohio State University，1999．

［8］ Lin G，Karniadakis G E．High-order modeling of micro-pulsed plasma thrusters［R］．AIAA 2002-2872．

［9］ Antonsen E L，Burton R L，Reed G A，et al．Effects of postpulse surface temperature on micro-pulsed plasma thruster operation［R］．AIAA 2004-3462．

［10］ Keidar M，Fan J，Boyd I D．Vaporization of heated materials into discharge plasmas［J］．Journal of Applied Physics，2001，89(6)．

［11］ Clark B L．An experimental and analytical investigation of Teflon abltion heat transfer parameters by the method of non-linear estimation［D］．Cornell University，1971．

［12］ Holzknecht B．An analytical model of the transient ablation of polytetrafluoroethylene layers［J］．International Journal of Heat and Mass Transfer，1977，20．

［13］ Arai N．Transient ablation of Teflon in intense radiative and convective environments［J］．AIAA Journal，1979，17(6)．

［14］ Gatsonis N A，Juric D，Stechmann D P，et al．Numerical analysis of Teflon ablation in pulsed plasma thrusters［R］．AIAA 2007-5227．

［15］ Kemp N H．Surface recession rate of an ablating polymer．［J］．AIAA Journal，1968，6(9)．

［16］ Spanjers G G，Lotspeich J S，McFall K A，et al．Propellant losses because of particulate emission in a pulsed plasma phruster［J］．Journal of Propulsion and Power，1998，14(4)．