非等温DSC法研究环氧树脂体系固化动力学①

李 恒，王德海，钱夏庆

(浙江工业大学化学工程与材料学院，杭州 310014)

0 引言

环氧树脂是一类重要的热固性树脂，其固化动力学参数对固化产物的结构、物理机械性能的优化及固化工艺的确定都具有理论指导作用。因此，固化动力学的研究具有重要的意义。等温和非等温DSC法是研究环氧树脂固化过程的重要方法，目前国内研究较多的是模型拟合法。环氧树脂的动力学模型主要包括n级动力学模型、自催化模型及 Kamal模型［1－2］。以模型为基础的动力学，不管是n级动力学或自催化模型，都是建立在活化能为常数的基础上。然而，环氧树脂的固化反应过程存在多个反应和扩散过程，反应机理复杂，表观活化能随固化反应的进程而改变，是固化度α的函数。所以，模型拟合法并不能很好地描述和预测环氧树脂的固化行为［3］。非模型动力学则可避免模型及模型参数选择不当造成的误差［4］，且由于等温和非等温条件下拟合得到的动力学参数基本一致，可由非等温数据预测等温固化行为，近年来已成为国外学者的研究热点［5］。

非模型拟合法的基本假设是固化度相同时，固化速率仅与温度有关，其核心问题是将微分或积分信号转化为固化度［6］。Vyazovkin提出了非线性Vyazovkin(NLV)法，极大地推动了非模型拟合法的发展［7－8］。本文基于Vyazovkin法建立了非模型动力学，对环氧树脂体系在不同温度下的固化度和反应时间进行了预测和验证，并与n级动力学模型和传统预测固化条件的方法进行了比较。

1 实验

1．1 原材料

E-51型双酚A环氧树脂，上海树脂厂，环氧值为0．51～0．53;增韧甲基四氢苯酐 JS-20，上海成谊高新科技发展有限公司;2，4，6-三(二甲胺基甲基)苯酚(简写DMP-30)，常州山峰化工有限公司;端羧基液体丁腈橡胶(CTBN):上海立深行国际贸易有限公司。

1．2 试样的制备

环氧树脂体系为E-51/JS-20/DMP-30/CTBN=100/100/1．5/15，将各组分混合均匀，用于DSC测试。

1．3 仪器与测试

DSC采用Mettler Toledo DSC 1进行测试，对环氧树脂体系进行升温速率分别为5、10、15、20 K/min的动态扫描，温度范围为－40～260℃，验证动力学DSC测试以200 K/min的升温速率从室温快速升到验证温度，恒温不同时间后迅速降温，再以10 K/min的升温速率从0～260℃进行一次动态升温测试，获得未完全固化样品的残余放热焓值。所有测试均在流速为50 ml/min的高纯氮气气氛下进行。

2 结果与讨论

2．1 n级动力学模型及其验证

树脂固化反应的动力学研究大多采用唯象模型中的n级动力学模型:

式中 α为固化度;n为反应级数;k0为反应速率常数，与温度相关。

固化动力学参数如表观活化能和反应级数等对了解固化反应有着重要的作用。一般可通过Kissinger和Crane方程［9－10］对不同升温速率得到的DSC数据进行处理，可得到Ea、n、A等反应动力学参数，进而确定固化反应的n级动力学模型方程。

Kissinger方程:

式中 β为升温速率;Tp为峰顶温度;Ea为表观活化能。

图1为不同升温速率下的DSC曲线，表1为不同升温速率下的放热焓值ΔH、起始温度Ti、峰值温度Tp及终止温度Tf。

不同升温速率时，ln(β/Tp2)与(1/Tp)的关系见图2。线性拟合可得直线斜率，即为 －Ea/R，截距为ln(AR/Ea)，相关系数为 0．999 59，即可求出 Ea=66．70 kJ/mol和 A=1．751 ×104s－1。

图1 不同升温速率DSC曲线Fig．1 DSC curves of system at different heating rates

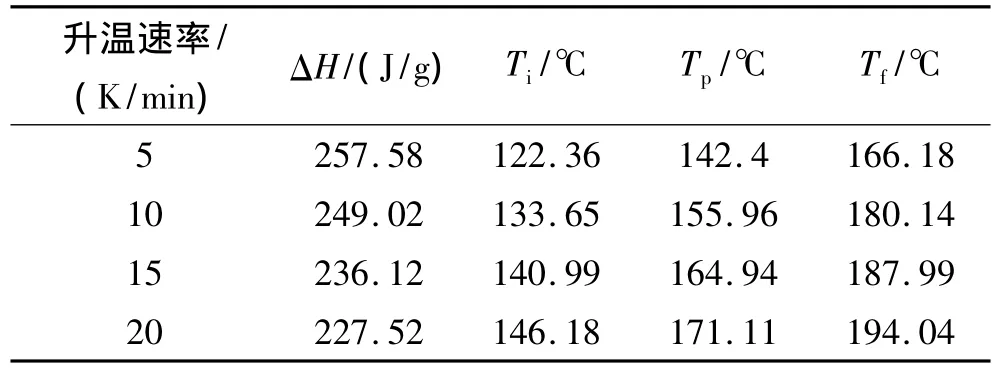
表1 不同升温速率下放热焓值ΔH、起始温度Ti、峰值温度Tp、终止温度TfTable 1 The respective values of thermal enthalpy ΔH，initial temperature Ti，peak temperature Tp，final temperature Tfat different heating rates

图2 ln(β/)与(1/Tp)的关系Fig．2 Relationship between ln(β/)and(1/Tp)

Crane方程:

图3 lnβ与1/Tp关系Fig．3 Relationship between lnβ and 1/Tp

结合前面求出的 Ea，即可求出 n=0．90，不是整数，表明该环氧树脂体系的固化反应为复杂反应。由所求的动力学参数可得出该树脂体系的n级固化动力学模型方程为

图4为升温速率为10 K/min时，通过n级动力学模型计算得到的dα/dt-T的关系曲线与实验值比较的曲线。从图4中可看出，n级动力学模型曲线与实验曲线有较大偏差，说明n级固化动力学模型不能很好地描述该环氧树脂体系的固化过程。

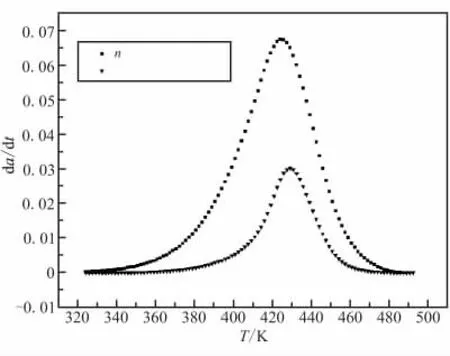
图4 实验值与n级动力学模型计算值比较Fig．4 The comparison of experimental and computed values by n order model

2．2 非模型动力学及其验证

非模型动力学是通过对多个升温速率得到的实验数据进行微分或积分的数学处理，得到固化度、活化能、时间之间的关系。非模型动力学的数学处理方法一般采用非线性Vyazovkin积分法(也叫NLV法):对于几个不同升温条件的DSC实验，当以下函数取得最小值时，此时的Ea值即为不同固化度时的活化能［9］:

本文采用Mettler Toledo公司的DSC1中自带的专业数学处理软件，对4条升温速率曲线的实验数据进行处理，可得到活化能和固化度的关系曲线，以及预测任何温度下固化度和时间的关系曲线。

对不同升温速率曲线进行非模型动力学(MFK)分析，便可得到活化能和固化度的关系曲线(图5)。

图5 活化能与固化度的关系曲线Fig．5 Curves of activation energy and curing degree

由图5中可见，表观活化能并不是一个定值，与固化度有一定关系。表观活化能随固化度的增加，先是迅速增大，然后基本保持稳定，最后在转化率90%时迅速增大。根据图5可得到固化度和恒温固化时间的关系，结果如图6所示。

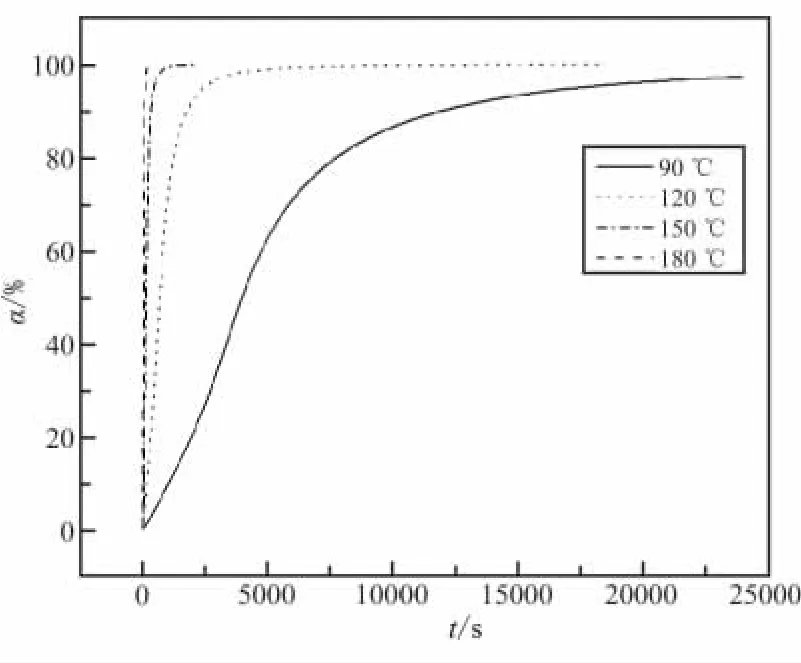
图6 任意温度下关于固化度和时间的预测曲线Fig．6 Prediction chart of relation between curing degree and time at different temperatures

为了对上述由非模型动力学方法预测的曲线进行验证，选取环氧树脂体系在90、120℃恒温温度下固化不同时间，迅速降温后，再以10 K/min进行一次动态升温，即可得到后固化焓值。结合表1中 ΔH0=249．02 J/g，利用公式 α =(ΔH0－ ΔHR)/ΔH0，就可算出固化度，且与预测曲线比较，结果见图7。

图7 不同温度下(90、120℃)实验值与预测曲线比较Fig．7 Comparison of MFK prediction and experimental values at different temperatures

由图7可看出，90℃和120℃下的实验值与预测曲线基本吻合，说明应用非模型动力学能很好地预测该环氧树脂体系的固化反应历程。

2．3 非模型动力学的应用

环氧树脂的固化温度随着升温速率的不同而变化，而树脂固化一般是在恒温下进行的，为确定环氧树脂的最佳固化温度，常采用T-β外推法［11］求得最佳固化温度的参数值。即以Ti、Tp、Tf对升温速率β作图(图8)，且线性拟合外推至β=0时，可得到3个特征温度，定义为凝胶温度Tgel、固化温度Tcure及后处理温度Ttreat。

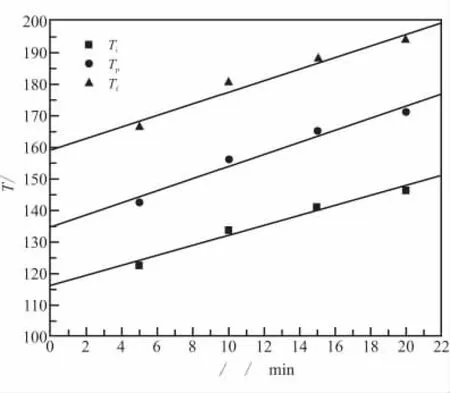
图8 T与β外推曲线Fig．8 Extrapolated curves of T and β

由图8中可看出，T和β呈线性关系。将3条直线外推至 β=0时，可得到 Tgel=116．04℃，Tcure=134．83℃，Ttreat=159．31℃。这种预测固化工艺参数的方法对固化温度具有一定的参考价值。文献［12］中，通过外推法得到的3个特征温度，即可确定最佳固化工艺为由起始固化温度116．04℃缓慢升温到134．83℃恒温固化，最后升温到159．31℃保持一段时间，使树脂完全固化。然而，这种固化工艺仍是一个升温过程，并在Tcure和Ttreat恒温的时间也没有说明。经过实验证实，在134．83℃下要达到95%的转化率至少需要15 min，但实际工厂生产考虑到能耗、效率等问题，是不可能采用135℃、15 min这样的固化工艺的。

根据验证，非模型动力学能很好地描述固化度与时间的关系。由预测曲线，对于该树脂体系，要达到95%的转化率，200、190、180、170、160、150 ℃分别需要0．74、1．13、1．76、2．80、4．56、7．59 min，考虑到温度太高，对设备要求较高，而且会增大树脂的内应力，综合考虑时间和温度，选择固化温度为170～180℃，固化时间为2～3 min。经实验测试，在此固化条件下，固化物能符合一定的力学性能要求。

3 结论

(1)采用非等温DSC法，能建立该环氧树脂体系的非模型动力学，通过不同温度(90、120℃)条件下验证。结果表明，与通过Kissinger、Crane方法建立的n级动力学模型相比，非模型动力学能更准确地描述和预测该环氧树脂体系的固化反应过程。

(2)与传统预测工艺的方法相比，非模型动力学的预测曲线能更方便、准确地为固化工艺设计和控制提供一定的参考价值。

［1］ 王焱，王先胜，陈海生．等温DSC法研究树枝状大分子PAMAM与环氧树脂的固化反应动力学［J］．高分子学报，2006(5):727-731．

［2］ Li S Y，Jarvela P．Application of a model-free isoconversional method to the cure of phenolic systems［J］．Journal of Polymer Science Part B-Polymer Physics，2001，39(13):1525-1528．

［3］ 廖栋，颜春，潘利剑，等．非等温DSC法研究苯并恶嗪树脂固化反应动力学［J］．热固性树脂，2011(1):1-5．

［4］ 甘丽，孙志杰，顾轶卓，等．升温与等温法非模型动力学研究环氧树脂固化反应［J］．高分子学报，2010(8):1016-1022．

［5］ Sbirrazzuoli N，Mititelu-mija A，Vincent L，et al．Isoconversional kinetic analysis of stoichiometric and off-stoichiometric epoxy-amine cures［J］．Thermochimica Acta，2006，447(2):167-177．

［6］ Vyazovkin S，Sbirrazzuoli N．Isoconversional kinetic analysis of thermally stimulated processes in polymers［J］．Macromolecular Rapid Communications，2006，27(18):1515-1532．

［7］ Vyazovkin S，Chen K．Increase in effective activation energy during physical aging of a glass［J］．Chemical Physics Letters，2007，448(4-6):203-207．

［8］ Vyazovkin S．Model-free kinetics-staying free of multiplying entities without necessity［J］．Journal of Thermal Analysis and Calorimetry，2006，83(1):45-51．

［9］ Kissinger E D．Reaction kinetics in differential thermal analysis［J］．Anal．Chem．，1957，29(11):1702-1706．

［10］ Crane L W，Dynes P J，Kaelble D H．Analysis of curing kinetics in polymer composites［J］．Polym．Lett．Ed．，1973，11(8):533．

［11］ Losada R，MIER J L，Barbadillo F，et al．Study of the cure of a diglycidyl-ether of bisphenol-a(DGEBA)/Triethylenetetramine(TETA)epoxy system by non-isothermal differential scanning calorimetry(DSC)［C］//VILARINHO P M．Advanced Materials Forum Iii，Pts 1 and 2．Zurich-Uetikon;Trans．Tech．Publications Ltd．2006:1094-1098．

［12］ 甘厚磊，易长海，吕鹏举，等．MOCA/环氧树脂体系的固化行为［J］．高分子材料科学与工程，2009(2):119-122．