自锚式悬索桥主塔稳定计算方法及影响因素分析

宋 凯

（上海市政工程设计研究总院（集团）有限公司，上海 200092）

1 概述

随着悬索桥跨径的不断增大，主塔高度的增加，主塔稳定分析成为控制悬索桥设计的控制因素之一。在悬索桥设计计算分析中，主塔在主缆约束下的稳定计算公式在规范中并未提及。对于传统的地锚式悬索桥，国内外学者已针对这个问题开展了许多研究[1]。自锚式悬索桥取消了传统悬索桥中所必须的巨大的锚锭，将主缆直接锚固在加劲梁上，使主梁直接承受主缆传来的水平力。全桥结构体系的改变，对主塔稳定分析产生了巨大的影响。本文以西宁市海湖新区文汇路跨湟水河大桥为例，研究了自锚式悬索桥主塔稳定分析的计算方法，并对影响因素做出一定探讨。

西宁市文汇路跨湟水河大桥为两塔五跨混凝土自锚式悬索桥，跨径布置为（24+65+158+65+24）m，全桥长度336 m，主跨及边跨为悬吊结构。主塔采用门式塔框架结构，总高51 m。全桥两根主缆，双缆面均为垂直索面，主缆水平距离19 m，吊索纵向间距为6 m。梁采用单箱三室混凝土鱼腹梁，梁高2.2 m，顶宽27.3 m。锚固墩和边墩处设置竖向支座，桥塔处设置竖向支座和横向抗风支座。图1为全桥总体布置图，图2为主塔构造示意图。

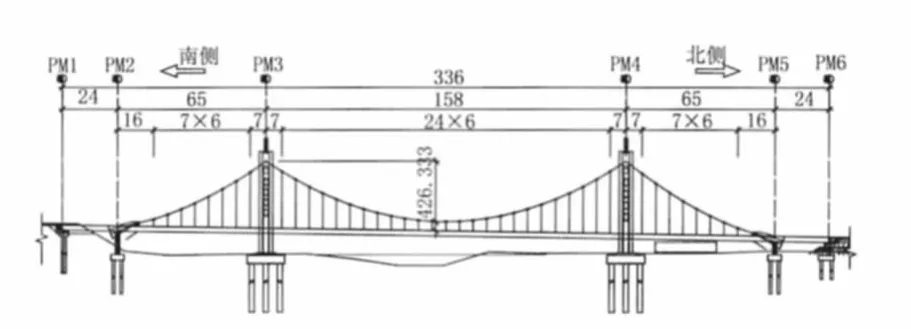
图1 总体布置图（单位：m）

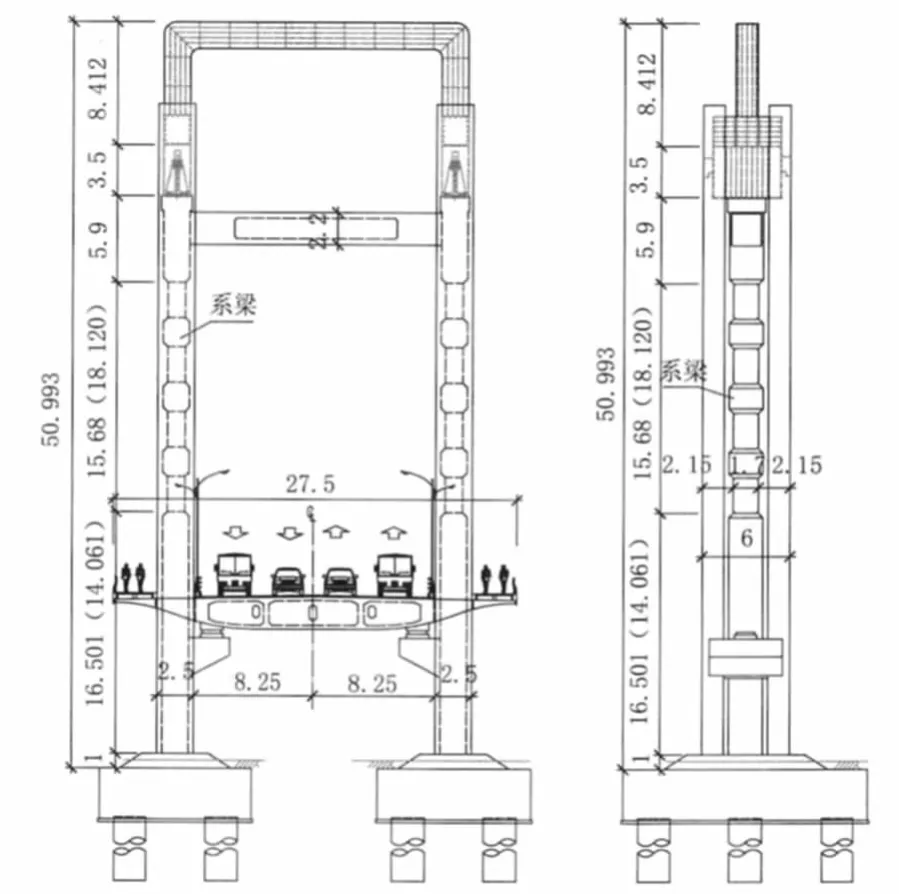
图2 主塔立面和侧面图（单位：m）

2 主塔稳定计算方法

结构失稳是指在外力作用下结构的平衡状态开始丧失稳定性，稍有扰动则变形迅速增大，最后使结构遭到破坏。稳定问题分为两类。第一类为平衡分支稳定，结构达到临界荷载时，除结构原来的平衡状态理论上仍然可能外，出现第二个平衡状态。第二类是结构保持一个平衡状态，随着荷载的增加在应力比较大的区域出现塑性变形，结构变形也很快增大，当荷载达到一定数值时，即使不再增加，结构变形也自行迅速增大而使结构破坏。实际工程中的结构稳定都属于第二类，但是第一类稳定问题力学模型单纯明确，其临界荷载又近似地代表相应的第二类稳定的上限，因此在理论分析中占有重要地位[2]。

对于两端铰支的受压杆件，其挠曲线微分方程：

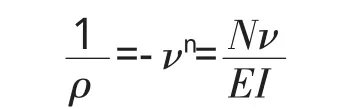
式中，ρ为曲率半径；E为弹性模量；I为截面惯性矩。

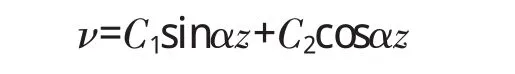
根据边界条件 z=0，ν=0；z=l，ν=0，可得到杆件的临界力为：

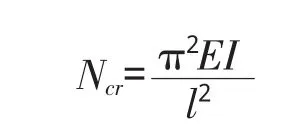
压杆稳定问题中，边界约束条件对临界力的大小有很大影响，不同支承情况下压杆的临界力与其计算长度的平方成反比，即对于一端固接、一端自由的压杆，计算长度βL=2L[2]。

对于一般构件，线性稳定问题可用直接积分法计算，对于较复杂的结构，则采用有限单元法更适宜。计算时可先用直接刚度法将各单元的刚度矩阵（含几何刚度矩阵）集合成结构刚度矩阵，并建立结构的平衡方程进行求解，即在整体结构模型中考虑局部杆件的稳定问题。

3 工程计算实例

西宁市文汇路跨湟水河大桥为两塔五跨混凝土自锚式悬索桥，全桥采用半漂浮体系，在主塔牛腿处设置纵向滑动支座，主梁与桥塔之间设置横向抗风支座，在边墩和锚墩处设置纵向活动支座及横向抗震挡块。针对该工程，建立有限元模型如图3所示。

图3 全桥结构有限元模型

去掉主梁和主缆等结构，仅保留主塔，在塔身施加轴力以考虑结构中几何刚度的影响。在塔顶施加单位力，计算得到裸塔顺桥向稳定临界力为2078 MN。此时力学模型为塔底固定，塔顶自由的悬臂压杆，杆件计算长度βL=2L。

图4为裸塔模型一阶纵向失稳模态图示。

裸塔模型中，仅仅考虑了由于塔身内轴力的存在而造成刚度的变化，即结构的几何刚度，没有考虑全桥结构其他构件对主塔刚度的影响，特别是塔顶主缆对压杆顶部约束的影响，因此不能反应结构的真实稳定状态。只有将全桥结构作为一个整体，分析结构整体稳定，找到主塔失稳的第一阶振型，才能反应主塔稳定的真实状态。

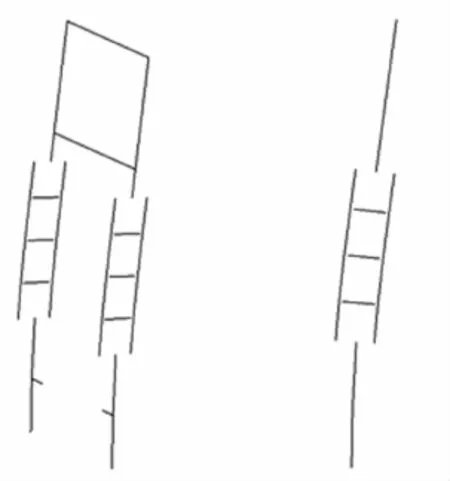
图4 裸塔模型一阶纵向失稳模态图示

在全桥整体模型中，在塔顶施加单位力，计算得到主塔顺桥向稳定临界力为3501 MN。杆件计算长度βL=1.54 L。

图5、图6分别为主塔一阶纵向失稳模态的透视图和立面图。

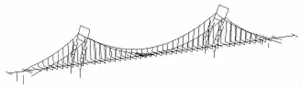
图5 主塔一阶纵向失稳模态（透视图）

图6 主塔一阶纵向失稳模态（立面图）

计算显示，对于主塔顺桥向稳定临界力，是否考虑结构总体刚度的因素，对结果影响比较大，杆件计算长度从2 L变为1.54 L，说明主缆对主塔的约束作用较为明显。

4 主塔稳定计算影响因素

从以上分析可以看出，在结构尺寸保持不变的前提下，主塔纵向稳定计算受边界条件的影响很大。在实际工程实例中，往往会根据不同需求设置不同的约束条件[4]，主塔的稳定临界力也会随之变化。

改变全桥约束体系，将塔梁处约束改为纵向固定支座和塔梁固接，分别计算得到临界力和计算长度系数β，如表1所列。

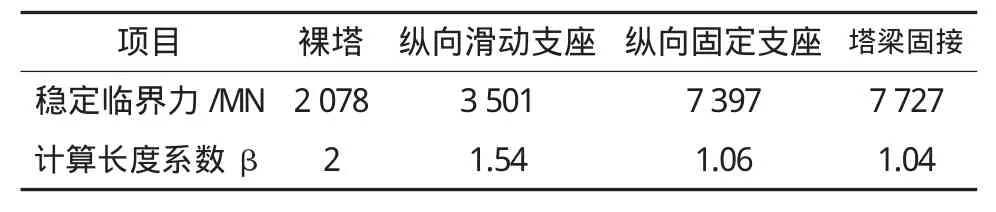
表1 计算长度系数β一览表

图7、图8分别为塔梁固定支座条件下与塔梁固接条件下，主塔一阶失稳模态图示。

图7 塔梁固定支座条件下主塔一阶纵向失稳模态图示

图8 塔梁固接条件下主塔一阶纵向失稳模态图示

分析显示，将全桥纵向约束以后，稳定临界力得到有效提高，主塔计算长度更短，其原因是因为全桥的纵向刚度增加，对塔顶约束更强，导致主塔纵向刚度增加。塔梁之间设置纵向支座和塔梁固接之间的差别很小，说明塔梁之间转动约束对主塔纵向刚度影响较小。

5 结论

自锚式悬索桥将大跨连续梁桥与悬索桥两种结构体系结合在一起，力学特性与传统地锚式悬索桥有所区别。本文分析了稳定计算原理，并以西宁市海湖新区文汇路跨湟水河大桥为例，分别针对不同边界条件计算主塔稳定临界力，得出以下结论：

（1）自锚式悬索桥的主塔稳定计算应放在全桥总体模型中进行，考虑全桥其他构件对主塔刚度的影响，方能真实反应实际结构中主塔的力学特性。

（2）主梁纵向约束条件对自锚式悬索桥的主塔稳定计算影响较大。当塔梁之间设置纵向约束时，主塔稳定临界力相比纵向滑动体系提高较多。塔梁之间的转动约束对主塔稳定影响相对较小。

[1]铁道部大桥工程局桥梁科学研究所.悬索桥[M].北京：科学技术文献出版社，1996.

[2]李国豪.桥梁结构稳定与振动（修订版）[M].北京：中国铁道出版社，2003.

[3]许世展，高传明，贺拴海，刘来君.悬索桥主塔纵向稳定的实用计算[J].长安大学学报（自然科学版），2005，（1）.

[4]常付平.主梁纵向约束方式对单塔自锚式悬索桥结构设计的影响[J].桥梁建设，2010，（6）.