蝴蝶拱空间受力特点及承载能力研究

吴 朴 ，胡欣科 ，谢 旭

（1.浙江大学建筑设计研究院,浙江杭州 310058;2.浙江大学,浙江杭州 310058）

0 前言

一般下承式拱桥，拱肋平行，桥面荷载通过横梁传递至系梁，系梁将部分荷载传递给吊杆，再由吊杆传递给主拱结构，最后由主拱圈将荷载传递至拱脚支座，拱肋受力基本为面内偏心受压，拱脚处拱肋和系杆承受竖向力、水平推力及面内弯矩。

随着社会经济发展，常规下承式的拱桥已经不能满足公众对桥梁美观性的要求，在此背景下，蝴蝶拱应运而生，这是一种的梁拱组合钢结构桥，结构内力由梁和拱联合分担，两片拱肋截面形状和几何参数各异，似蝴蝶向两侧非对称外倾，吊杆呈倾斜空间布置，拱肋除了受到轴向力外，还受到双轴的弯矩共同作用，主梁拱脚部位受力非常复杂，其承载能力已经不能通过平面内或者平面外的失稳来评价。

迄今国内外学者对钢拱肋的稳定及承载能力问题作了大量研究，Kuranishi[1-3]、Yabuki[4-6]等人通过大量数值分析，建立了以压杆稳定理论为基础的两铰拱，以及无铰钢拱桥非弹性稳定强度计算式，为结构设计提供了强度验算方法,万鹏[7]分析了刚拱肋初始缺陷、横向位移、横撑参数，以及梁拱横向刚度比的变化对钢拱的承载能力的影响。程霄翔[8]对异型钢管混凝土拱桥的稳定问题进行了深入的研究，同时提出常用的空间系杆模型的失真，进而建立了基于响应面的模型修正技术，谢旭[9]通过对大跨度两铰钢拱桥的研究，比较了加载方式对结构承载能力计算结果的影响，

这些研究采用弹性和弹塑性的分析方法，基本基于杆系结构计算模型，不能考虑钢板局部失稳的影响，同时，受到计算模型的局限性，不能精确模拟拱肋塑性扭转的影响。

为了研究蝴蝶拱的空间受力特点和极限承载能力，本文以一座实际桥梁为对象，建立三维有限元模型，通过弹塑性及几何非线性分析，对其极限承载能力进行了精细化的研究，为同类结构的桥梁设计提供参考。

1 桥梁概况

浙江省丽水市鼎湖大桥位于缙云县，跨越好溪，主桥采用一跨90 m的蝴蝶钢拱钢梁组合体系桥，设计荷载城-A级，人群3.5 kPa，设计车速60 km/h，双向4车道。主桥的横断面布置：6.75 m～11.4 m（人行道+镂空吊索锚固处）+8.25 m（机非混行车道）+2.5 m（中央分隔带）+8.25 m（机非混行车道）+8.25 m～12.9 m（人行道+镂空吊索锚固处），图1为全桥结构布置图。

主桥横桥向共设2片钢拱肋，其中大拱肋向外倾斜，倾斜角度为16°，大拱肋拱轴线在其自身倾斜面内为二次抛物线，矢高为28 m，跨径为87 m，矢跨比为1/3.107。截面采用矩形，全拱为变截面，由拱脚的2 m变至拱顶的1.2 m。

小拱肋向外倾斜，倾斜角度为20°，小拱肋拱轴线在其自身倾斜面内为二次抛物线，矢高为18 m，跨径为87 m，矢跨比为1/4.833。截面采用矩形，全拱为等截面，截面高为1.5 m。

桥面系采用钢箱梁结构，顶板采用带U肋加劲正交异性桥面板，底板采用L型肋加劲，车行道顶板钢板厚度为16 mm,底板为14 mm，人行道顶板钢板厚度为12 mm,底板为12 mm，在主吊杆锚固点附近局部加厚，全桥纵向共设置纵梁7道，纵梁厚度20 mm。顺桥向每4 m设置一道横梁。

支座处的端横梁宽3 m，为箱梁断面，顶板、底板、腹板厚均为60 mm。

主桥吊杆水平布置间距4.0 m，横向为4排，主吊索采用73φ5 mm高强度镀锌平行钢丝，副吊索采用19φ5 mm。

图1 桥梁结构布置图（单位：m）

2 计算模型及参数

该桥计算采用ABAQUS有限元软件，拱肋和桥面采用板壳单元，吊杆采用杆单元，选择弹塑性及几何非线性分析模型，图2为全桥计算模型。

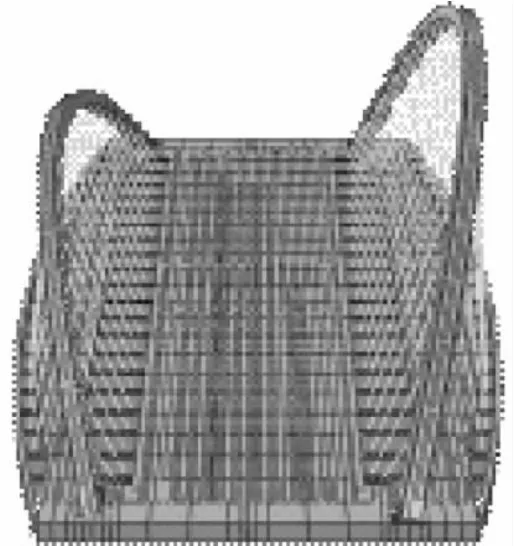
图2 全桥有限元计算模型

荷载包括恒载和活载及吊杆初始张拉力。活载包括车道荷载与人群荷载。车道荷载按车道宽度换算成均布荷载加载。

非线性计算利用弧长增量法，按比例增加作用荷载计算结构的极限承载能力，以成桥状态作为加载开始的初始状态。加载取了四种典型的工况：满布荷载、半跨满布荷载、大拱侧半幅满布荷载、小拱侧半幅满布荷载。

钢材的弹性模量为2.06×105MPa，泊松比为0.3，屈服强度为345 MPa，吊杆的弹性模量为1.95×105MPa，屈服强度为 1 650 MPa，抗拉强度为1 860 MPa。屈服后的弹性模量均取屈服前的1%，以考虑材料强化的影响。

3 计算结果及分析

3.1 四种荷载工况下的结构应力状态

通过分析四种工况下的应力结果，发现最大应力主要出现在拱肋的拱顶内侧和拱脚的外侧，及主梁的拱脚位置（靠近跨中侧），其中在满布荷载作用下，到达最大值。图3为满布荷载作用下的应力分布，其中小拱肋内侧拱顶的平均应力水平为40 MPa,小拱肋外侧拱脚平均应力水平为60 MPa，主梁拱脚位置（靠近跨中侧）平均应力水平为40 MPa。大拱肋内侧拱顶的平均应力水平为45 MPa,小拱肋外侧拱脚平均应力水平为48 MPa，主梁拱脚位置（靠近跨中侧）平均应力水平为30 MPa。

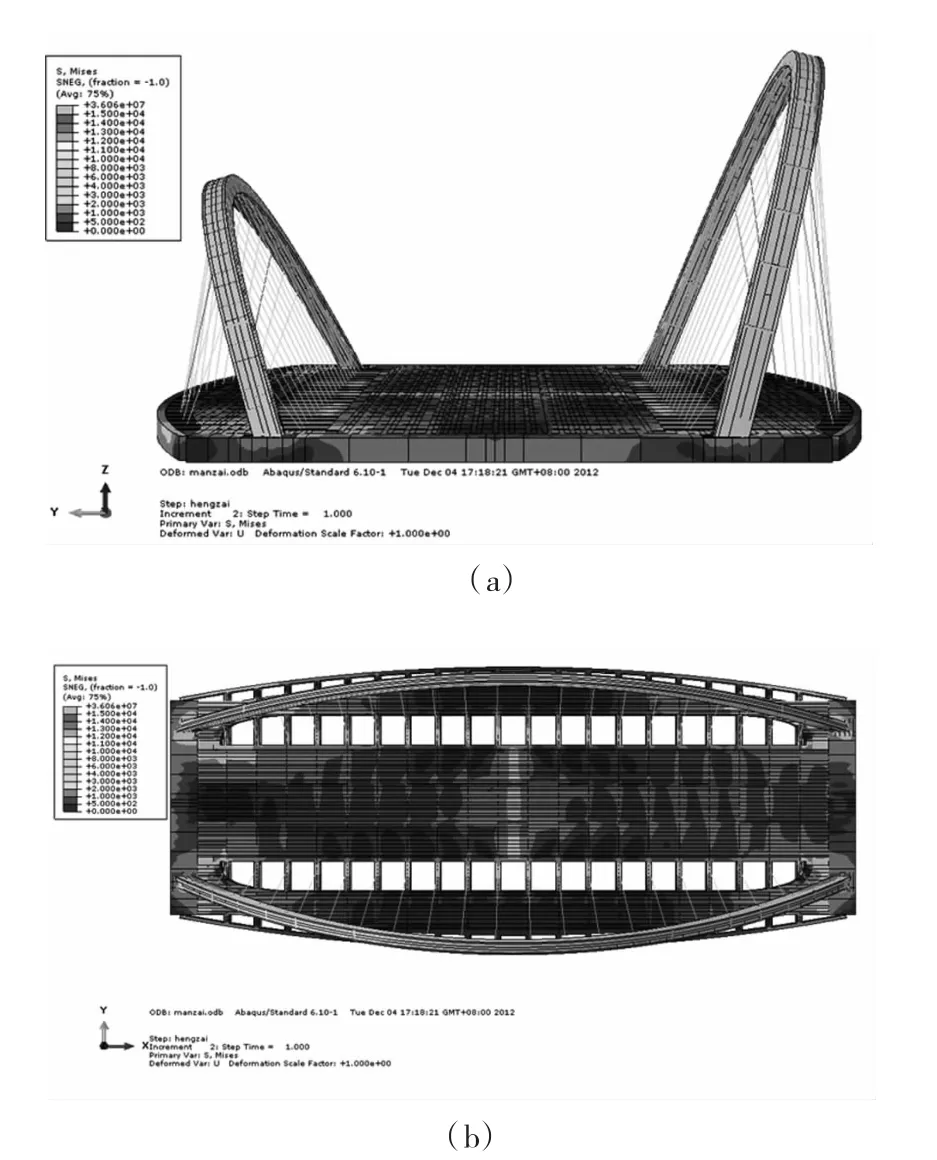
图3 满布荷载工况荷载系数最大时的结构应力图示

3.2 四种荷载工况下的结构变形

图4～图7为四种工况下荷载到达最高点时的结构变形形状和原始形状的对比图，从整体来看，四种工况下均以发生拱肋外侧方向的变形和主梁人行道跨中下挠为主，满载作用下主梁变形最大，此时小拱肋人行道跨中挠度为5.1 cm，小拱肋侧向变形为4.6 cm。同时在小拱肋偏载作用下小拱肋的拱顶侧向变形也接近了4.6 cm，说明偏载对拱肋整体变形的影响比较大。

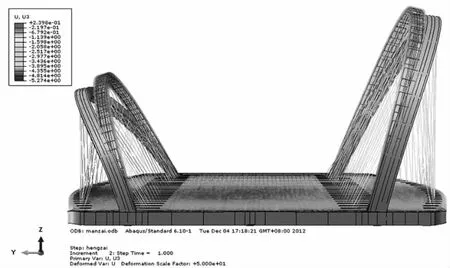
图4 满布荷载工况荷载系数最大时的变形图示

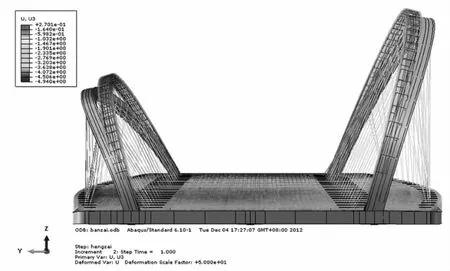
图5 半跨满布荷载工况荷载系数最大时的变形图示

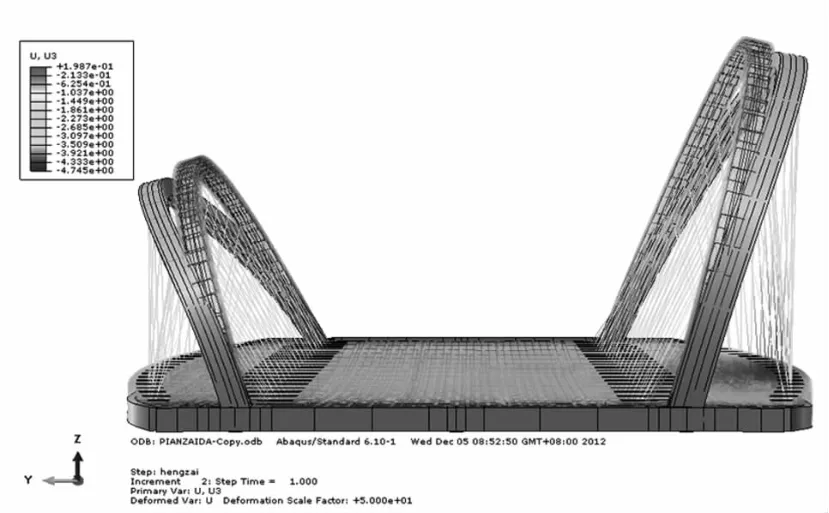
图6 大拱半幅满布荷载工况荷载系数最大时的变形图示

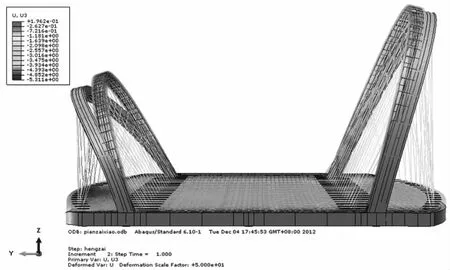
图7 小拱半幅满布荷载工况荷载系数最大时的变形图示

4 拱肋的极限承载能力研究

拱肋的极限承载能力由拱肋和吊杆共同决定。首先分析拱肋的局部失稳对承载能力的影响，这里以变形比较大的满载和小拱肋偏载两种工况下小拱拱顶截面为对象分析截面的变形过程。

图8、图9为满载和小拱肋偏载两种工况下的计算结果，可见，拱肋在向外侧的变形过程中，屈服前截面的变形不明显，随着荷载增大，拱顶截面以整体外侧变形为主，达到极限荷载时，截面的变形仍不大，未发生局部失稳。达到极限荷载之后，满载工况下随着荷载继续增大，拱肋内外侧的表面钢板未突起，说明拱肋未发生局部失稳。

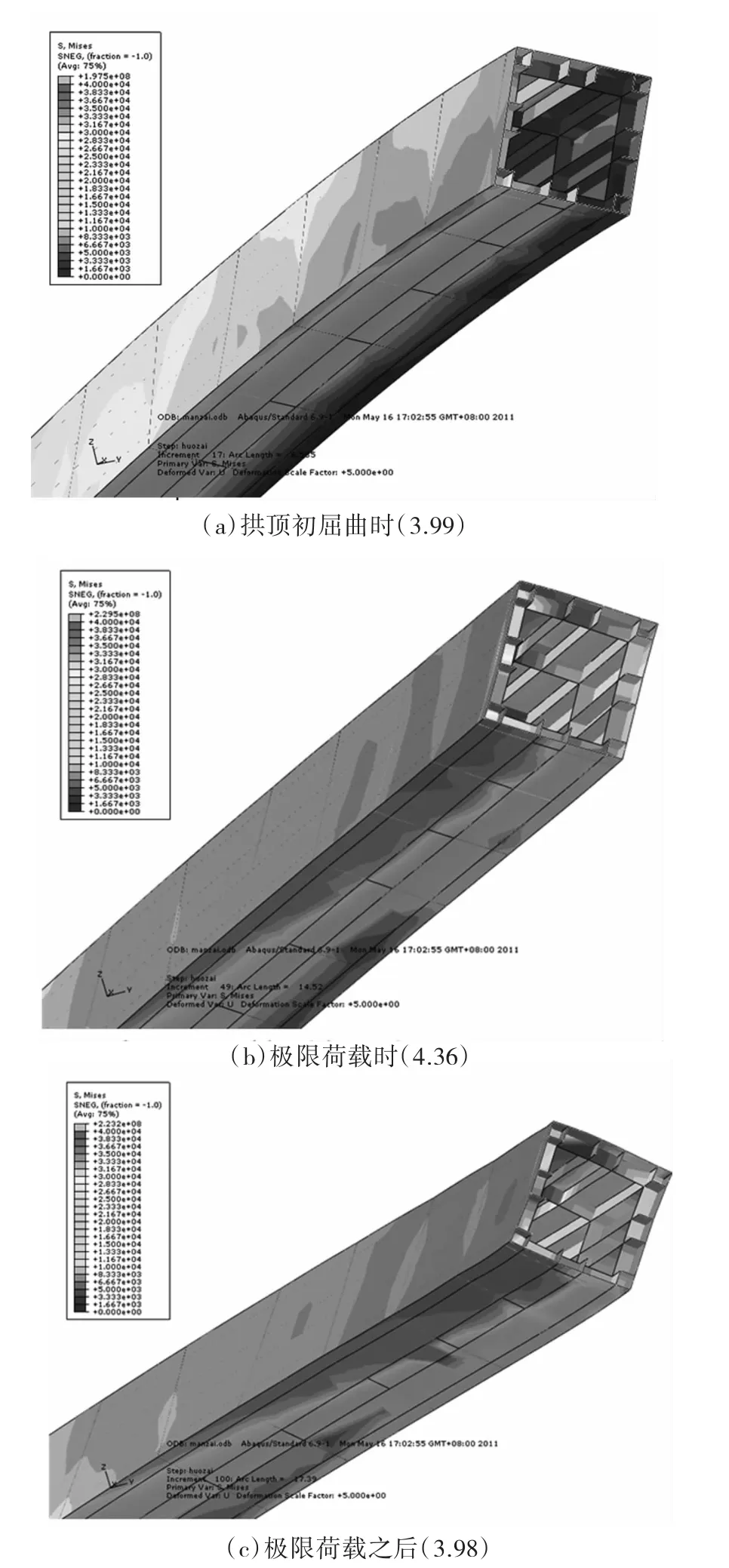
图8 满布荷载工况小拱顶截面变形图

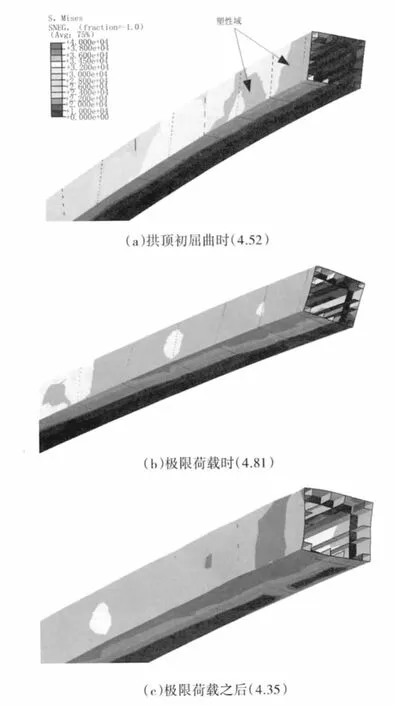
图9 小拱半幅满布荷载工况小拱顶截面变形图

而在小拱肋偏载作用下，在无横隔板处，内侧的表面钢板向外侧突起，上下表面的钢板分别向上下突起，说明拱肋发生了局部失稳。

从上述两种工况下的拱肋变形过程分析，说明拱肋局部变形发生在整体失稳以后，钢板局部失稳对结构整体失稳不起控制，结构发生屈服型的破坏形式。

图10为大拱拱顶截面在满布荷载工况下的荷载系数(k)-竖向位移(d)曲线，其中荷载系数为0时对应结构成桥初始状态。从计算结果发现，大拱肋初屈服的荷载系数为3.71，极限荷载系数为4.36，拱肋在进入极限状态以后没有发生明显的承载能力下降现象，这是由于吊杆对拱肋侧向变形的约束作用引起的，

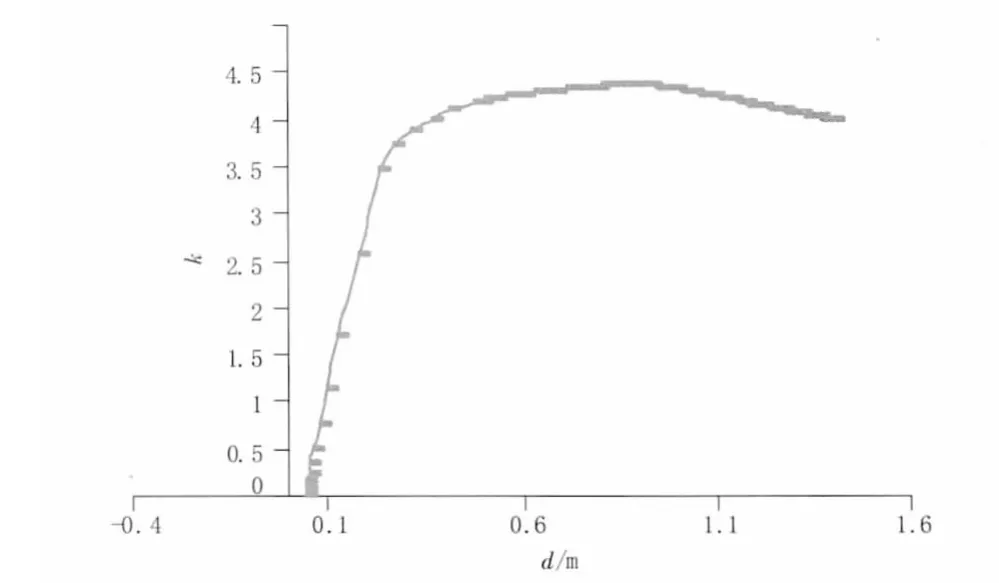
图10 满布荷载工况大拱肋拱顶荷载-位移曲线图

图11为满载工况大拱肋内侧吊杆拉应力变化图。吊杆的初屈服荷载系数为3.45,最先进入屈服阶段（主拉应力达到1 650 MPa）的吊杆为跨中的1号吊杆，当结构达到极限荷载状态之前（4.36），内侧吊杆已经全部屈服（主拉应力达到1 650 MPa），但未达到抗拉强度（1 860 MPa）。在达到极限荷载之后，局部吊杆出现卸载现象。

图11 满布荷载工况大拱内侧吊杆应力变化曲线图

从上述数据分析，得出吊杆的初屈服是发生在拱肋初屈服之前，说明吊杆的初屈服有可能导致拱肋的初屈曲。在所有内侧吊杆屈服后，拱的侧向变形约束刚度有所下降，导致整桥迅速达到极限荷载状态。吊杆刚度对结构的极限承载能力有很大的影响。

5 结论

通过精细的三维全桥模型计算分析根据分析，得到以下几点结论：

（1）拱肋在满布荷载作用下受力最为不利，主应力最大主要出现在拱肋拱顶内侧和拱脚的外侧，以及主梁的拱脚位置（靠近跨中侧），因此拱脚处的拱肋和桥面均应进行特殊的加强设计。

（2）拱肋的局部失稳对结构整体极限承载能力不取控制作用。

（3）吊杆的刚度对拱肋极限承载能力有一定影响。

[1]Kuranishi S,Lu L W,Load carrying capacityof two hinged steel arches,Proc.of JSCE,1972，No.204:129-140.

[2]Kuranishi S,Sato T,Otuski M,Load carrying of two hinged steel arch bridges with stiffening deck,Proc.of JSCE,1980，No.300：121-138.

[3]Kuranishi S,Yabuki T,Ultimate strength design criteria for two-hinged steel arch structures,Proc.of JSCE Structural Eng./Earthquake Eng.,1984，1(2):115-123.of Structural Engineering,1984，110(9):2263-2274.

[4]Yabuki T,Kuranishi S,Out-of-plane behavior of circular arches under side loading,Proc.of JSCE,1973，No.214:71-82.Eng./Earthquake Eng.,1987，4(1):141-149.

[5]Yabuki T,Kuranishi S,In-plane ultimate strength of deck-type fixed-end arch bridges,Proc.of JSCE Structural Eng./Earthquake Eng.,1989，4(2):205-216.

[6]YabukiT,KuranishiS,Evaluation ofstability strength for deck-type steel arch bridges,Structural Eng./Earthquake Eng.,JSCE,1993，10(3):117s-127s.

[7]程霄翔，异形钢管系杆拱桥稳定性与极限承载能力研究[D].南京：东南大学，2010.

[8]万鹏，大跨度钢拱桥极限承载力综合三因素检算方法研究[D].成都：西南交通大学，2005.

[9]谢旭,李辉,黄剑源,大跨度两铰钢拱桥面内稳定分析[J].土木工程学报,2004，（08）.