复合场内斜面上的最佳抛射角

杨月春

(中国石油大学河南濮阳学习中心 河南 濮阳 457001)

王秀娥

(春湾中学 广东 阳江 529616)

仇小慧 曹锦慧 马秀君 王萍 韩春霖

(中国石油大学河南濮阳学习中心 河南 濮阳 457001)

1 复合场内沿斜面上升方向顺场抛射带电质点

如图1所示，空间存在水平向右的匀强电场，有一带正电的质点自O点沿斜面上升方向以抛射角α(抛射方向与斜面间的夹角)抛出，不计空气阻力，要使质点落在斜面上距离抛射点最远的地方，抛射角α应为多大？

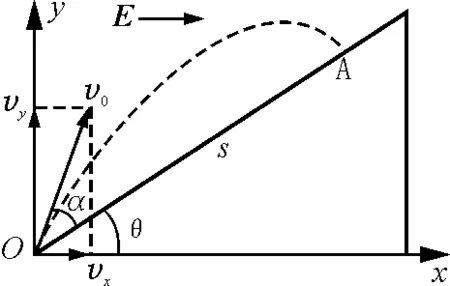
图1

解析：质点抛出后，在重力场和电场组成的复合场内运动，运动轨道曲线与斜面的交点A即为质点的落地点. 图中OA之长s就是物体沿斜面的射程，使s最大的角度α即为最佳抛射角.

取点O为坐标原点,水平向右方向为x方向，竖直向上方向为y方向，建立直角坐标系xOy.质点沿两方向的运动方程为

式中a为质点沿水平方向向右的加速度，由电场力的大小决定.将式(1)两边乘以g，式(2)两边乘以a再相加，求出t，得

(3)

将式(1)两边乘以sin(α+θ)，式(2)两边乘以cos(α+θ)，再相减，求出t2

(4)

结合式(3)、(4)得

整理该式得

[xsin(α+θ)-ycos(α+θ)]

(5)

式(5)就是质点运动的轨道方程.

直线OA的方程为

y=xtanθ

(6)

点A是质点运动轨道曲线和直线OA的交点，其坐标值可由式(5)、(6)联立解出

[sin(α+θ)-tanθcos(α+θ)]·

(g+atanθ)-2

[sin(α+θ)-tanθcos(α+θ)]·

(g+atanθ)-2cos-1θ=

(7)

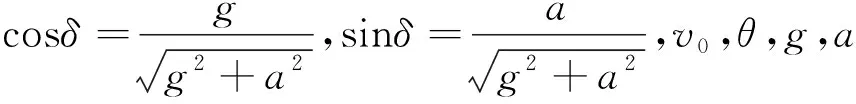
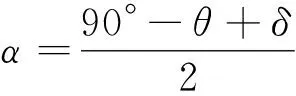
据此得最佳抛射角

(8)

所对应的最大射程为

也就是说，最大射程不仅与v0，θ有关，还与a(同时与δ)有关，亦即与质点所受电场力大小有关，而最佳抛射角仅与θ，δ有关，与v0无关.

讨论：

(1)在式(7)中，若取a=0(同时δ=0)，θ≠0，就得无电场时斜面上斜抛物体的射程

(2)在式(7)中，若取a≠0(同时δ≠0)，θ=0，就得有电场时水平面上斜抛物体的射程

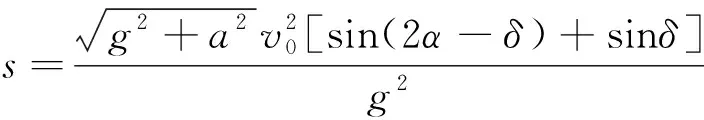
(3)在式(7)中，若取a=0(同时δ=0)，θ=0，就得无电场时水平面上斜抛物体的射程

最佳抛射角为45°.

2 复合场内沿斜面上升方向逆场抛射带电质点

在图1中，如果空间存在水平向左的匀强电场，即逆场抛射，质点抛出后沿两方向的运动方程为

用类似的方法求出质点在斜面上的射程

(11)

最佳抛射角

(12)

利用式(11)同样可以得出3种特殊情况下的射程和最佳抛射角.

3 复合场内沿斜面下降方向顺场抛射带电质点

如图2所示，空间存在水平向左的匀强电场，将带正电的质点自点O沿斜面下降方向以抛射角α抛出.

图2

质点沿两方向的运动方程为

用类似的方法求出质点运动方程，再结合直线OA的方程

y=-xtanθ

(15)

求出质点在斜面上的射程

(16)

最佳抛射角

(17)

利用式(16)同样可以得出3种特殊情况下的射程和最佳抛射角.

4 复合场内沿斜面下降方向逆场抛射带电质点

在图2中，如果空间存在水平向右的匀强电场，即逆场抛射，质点抛出后沿两方向的运动方程为

用类似的方法求出质点在斜面上的射程

(20)

最佳抛射角

(21)

利用式(20)同样可以得出3种特殊情况下的射程和最佳抛射角.

1 杨月春，洪雪芹，戴景生.斜面上任意抛射的最佳抛射角.大学物理，2008,27(5)：12～14

2 杨月春，王秀娥,等.对斜面上最佳抛射问题的进一步研究.物理通报，2012(8)：94～98

3 严导淦.物理学.北京:高等教育出版社，2003

4 李椿，夏学江.大学物理.北京:高等教育出版社，1997