浅析二元一次不定方程及其解

韩孝明

（吕梁学院汾阳师范分校，山西 吕梁 032200）

不定方程是数论中最古老的一个分支，也是数论中一个十分重要的研究课题，我国古代对不定方程的研究很早，且研究的内容也极为丰富，在世界数学史上有不可忽视的地位。如《张丘建算经》中的“百钱买百鸡”问题、《九章算术》中的“五家共井”问题等等，中外驰名，影响甚远。在公元3世纪初，古希腊数学家丢番图曾系统研究了某些不定方程问题，因此不定方程也叫做丢番图方程。

一、不定方程定义

所谓不定方程，是指未知数的个数多于方程的个数且其解受到某种条件的限制的方程或方程组。

不定方程领域中的基本问题是：不定方程有无整数解，有多少整数解，如何求出整数解。围绕这些问题，至今存在着大量的未解决问题，因此不定方程仍是一个很活跃的数学领域。中小学的数学竞赛也常常因为某些不定方程的解法巧妙而引入不定方程问题。

二、二元一次不定方程及其解

形如 ax+by=c(a，b，c∈z，ab≠0)的方程称为二元一次不定方程。求其整数解的问题叫做解二元一次不定方程。

由于方程的解x、y可以是正整数，也可以是负整数，或者零，所以我们可以只讨论a、b都是正整数的情况。例如，3x-2y=1与3x+2y=1的解相比较，y的值只差一个负号。

当 c=0时，如果(a，b)=d（a、b的最大公约数为 d），那么在方程的两边同时除以d,使x、y的系数互质。因此不妨假设(a，b)=1，解方程得x=-，由于(a，b)=1，因此当y能被a整除时，方程ax+by=0才有整数解。所以可令y=at（t为任意整数），这时x=-bt，即方程 ax+by=0的一切整数解为（其中t为任意整数）

当c≠0时，实际上也只需要讨论c＞0的情况。因为当c＜0时，我们可以在方程两边同时乘以-1，这样方程ax+by=c的右边就成为正整数了。因此对于二元一次不定方程，可以只讨论a＞0、b＞0、c＞0的情况。

现在我们研究二元一次不定方程在什么条件下才有整数解。先考察下面几个方程有没有整数解：2x+y=10，4x+2y=20，4x+2y=25。对于方程 2x+y=10，通过观察可以知道，x=1,y=8是这方程的整数解，因此这个方程有整数解。

对于方程 4x+2y=20，方程两边同时除以2，得2x+y=10，因此这个方程也有整数解。

对于方程4x+2y=25，由于4x+2y=2(2x+y)为偶数，而25是奇数，因此这个方程没有整数解。

对于方程2x+y=10来说，x、y的系数互质，上面已经指出这个方程是有解的；对方程4x+2y=20来说，虽然x、y的系数不互质，但它们的最大公约数2能整除20，这是方程也有解；对方程4x+2y=25来说，x、y的系数不互质，且它们的最大公约数2不能整除常数项20，这时方程无解。这些特点虽然是从一些具体的不定方程归纳出来的，但是它对一般不定方程也是适用的。我们有下面定理：

定理1：二元一次不定方程ax+by=c(a,b,c∈N*)有整数解的充要条件是d│c（其中d=(a,b）。

证明：一是必要性。如果方程ax+by=c有整数解x=x0，y=y0，则 ax0+by0=c，因为 d│a,d│b,所以 d│(a x0+by0),即 d│c。二是充分性。因为 d│c，所以 c=dq,由裴蜀恒等式可以知道，存在两个整数x0，y0，使a x0+b y0=d。

在上式两边同时乘以 q，得 a x0q+b y0q=dq即a x0q+b y0q=c。

因此方程ax+by=c有整数解x=x0q,y=y0q。

由上述定理可知，如果c不能被a、b的最大公约数整除，那么方程ax+by=c无解，且可在ax+by=c两端都约去d，使得(a，b)=1。所以通常二元一次不定方程的解是在a、b互质的情况下讨论的。

判断出一个二元一次方程有解以后，如何求出它的一切整数解呢？我们有下面的结论：

定理2：如果二元一次不定方程ax+by=c[(a,b)=1]有整数解x=x0，y=y0，则此方程一切解可以表示为

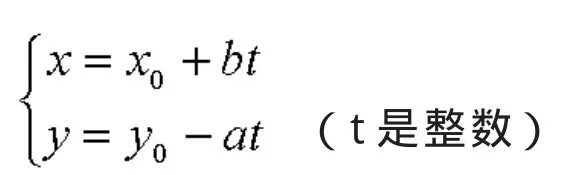
因为x=x0,y=y0是方程ax+by=c的整数解，所以ax0+by0=c，又因为 a(x0-bt)+b(y0+at)=ax0+by0=c。

再证明方程ax+by=c的任意一个整数解都可以表示成形式

设(x1,y1)是方程ax+by=c的任意一个整数解，则a x1,+b y1=c;

又由a x0+b y0=c，可得a(x1-x0)+b(y1-y0)=0，所以b│a(x1-x0)。

由于(a,b)=1，所以 b│（x1-x0），即 x1=x0+bt t∈z，所以 y1=y0-at t∈z。

由定理2可知，要求出二元一次不定方程ax+by=c的全部整数解，必须先求出它的一组特解。下面介绍几种求ax+by=c特解的方法。

方法一，观察法（或尝试法）：

观察法是根据已有经验，通过观察尝试求解的一种办法。

例如：方程2x+y=10很容易通过观察得出x=1,y=8是其一组特解。

方法二，辗转相除法：

辗转相除法是利用求最大公约数的逆推过程求特解的一种办法。

例如：解方程37x-107y=25。

解:因为(37,107)=1，1│25，所以此方程有解。

用辗转相除法求特解107=37×2+33，37=33×1+4 33=4×8+1，从最后一个式子向上逆推，得到37×(-26)-107×(-9)=1，所以 37×(-26×25)-107×(-9×25)=25，

方法三，整数分离法：

整数分离法是用系数较大的未知数表示系数较小的未知数，从而求解的一种办法。

例如：求方程7x+19y=213的一组解。

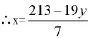
要使得x、y取整数，只需k取适当的值，使3-5k能被7整除。通过观察与估算可知，当k取2时=-1。由此得x=30-2k=25。

因此，原方程的一组整数解是x=25，y=2。

方法四，同余法：

同余法是利用解同余式的方法求二元一次不定方程解的一种办法。

例如：求9x+16y=35的解。

解：把原方程改写成同余式16y≡35(mod6)，

解之，可得 y≡5(mod9)，所以 y=5+9t(t为任意整数)；

把y=5+9t代入原方程，得x=-5-16t，

综上所述，仅是对二元一次不定方程及其解的初步认识，关于不定方程中还有很多未解之谜，望有兴趣者共同探讨。

[1]陈肇曾.数论初步[M].北京：高等教育出版社，1996.

[2]王元.初等数论[M].北京：人民教育出版社，2003.

[3]王进明.初等数论[M].北京：人民教育出版社，2002.