极限运算方法研究
2013-01-11朱美玲
太原城市职业技术学院学报 2013年1期
朱美玲
(太原城市职业技术学院,山西 太原 030027)
极限的求解是高等数学基本运算之一,其包含的类型多,方法技巧性强,论文介绍几种求极限常用的方法。
一、直接代入
初等函数在其定义域内某点的极限等于函数在该点的函数值,即求连续函数的极限,可归结为计算函数值。
二、消去零因子
1.分解因式
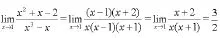
2.通分

3.有理化


三、比较次数
其中,a0≠0,b0≠0。
四、无穷小
1.无穷小与有界函数的积仍是无穷小

2.利用无穷小与无穷大的倒数关系

3.等价无穷小代换
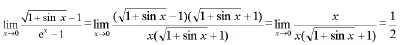
(当 x→0时,ex~x,sin x~x)
五、利用重要极限求极限
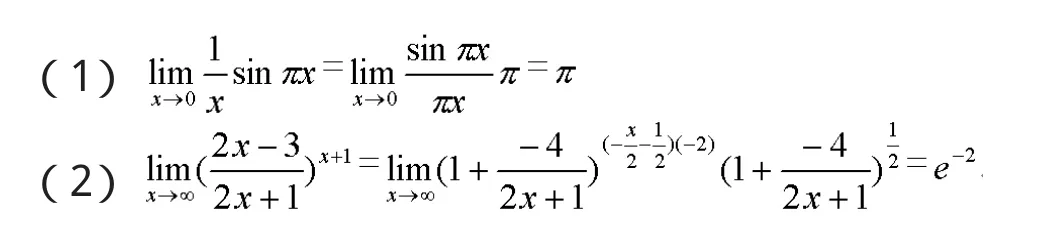
六、洛比达法则求极限
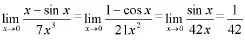
七、夹逼准则求极限
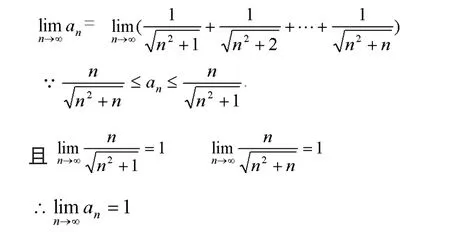
八、定积分求极限
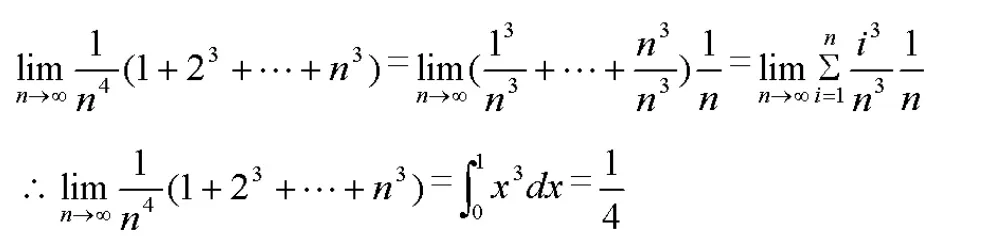
此外,还有利用泰勒公式求极限、柯西准则求极限等等。总之,求极限方法灵活多变,只有通过大量练习、及时总结,才能在解题当中根据题型迅速选择适当方法准确求解。
[1]叶志萍.洛比达法则运用中的弱点克服[J].大连民族学院学报,2002,(2).
[2]岳卫芬.利用极限的除法法则求f(x)/g(x)型的极限[J].高等函授学报(自然科学版),2005,(6).
