一种考虑应力洛德角剪切变形的三维双屈服面模型的初步研究
2013-01-11段新胜
王 硕, 段新胜
(中国地质大学(武汉) 工程学院, 湖北 武汉 430074)
本构模型的建立、计算及应用,在边坡、地下岩石隧道、水电开发和铁路、公路等工程建设中具有重要的实际应用意义。沈珠江[1]院士把现代土力学研究内容划分为应用土力学、实验土力学、计算土力学、理论土力学,并指出本构模型是现代土力学科分支领域核心基础。
自1963年,Rosco[2]等提出著名的剑桥模型,标志着土的本构理论发展进入新阶段。现在本构模型的种类已达到上百种,例如非线性弹性模型、内时本构模型[3](无屈服准则,主要优点不必建立不同材料的强度准则)、基于材料状态相关临界状态理论的本构模型[4]、基于热力学的本构模型[5]、统一硬化模型[6,7]、基于广义塑性力学的本构模型[8]以及引入智能算法的本构模型[9]。大部分模型是建立在屈服准则基础上,可以根据屈服面的多少,将模型简单划分为单屈服面、双屈服面、三重屈服面和多重屈服面模型。
单屈服面模型有两种:基于体积屈服面的剑桥模型和基于剪切变形的经典弹塑性模型。对于“帽子”模型,如剑桥及修正剑桥模型、Khosla模型等,能较好地反映土的体积屈服变形,而不能较好地反映剪切变形。对于经典弹塑性模型,如Mohr-Coulomb模型、Drucker-Prager模型、 Lade-Ducan[10]的“锥形”剪切屈服面模型等主要反映了剪切屈服,却没有充分反映体积屈服。以上单屈服模型都不能较好地同时考虑剪切变形与体积变形即土的剪胀与剪缩基本特性。
针对以上单屈服面模型的局限性,Drucker较早地提出了双屈服面模型概念,Prevost[11]、Baldi[12]、Lade[10]等发展了双屈服面模型。国内学者,沈珠江[13]提出了南水双屈服面模型、殷宗泽[14]根据土体微观变形机理提出一个实用的椭圆-抛物双屈服面模型。
相比单屈服模型,双屈面模型主要有两方面优点:一是能够同时较好地反映土的剪胀与剪缩特性;二是能够反映塑性应变增量方向与应力增量的相关性即相对于单屈服面,塑性应变增量方向不仅与土体单元所处的应力状态有关,而且与应力增量相关。
为了更好地说明土的塑性变形性质,沈珠江[15]基于“部分屈服面”的概念,提出了一个三重屈服面模型,杨光华[16]提出了土的本构模型的广义位势理论,对现有的各种建模理论探讨了其数学上统一的联系。郑颖人等[8]提出了既适合于岩土材料,也适合于金属的广义位势塑性力学。其中,广义塑性力学理论根据矢量原理,采用三个线性无关的势函数来拟合推导出广义塑性力学及多重势面理论。若采用为p,q,θσ塑性函数时, 相应的三个屈服面为:
(1)
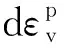
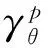
(2)
此前,大部分双屈服模型及沈珠江的三重屈服面模型均没有体现出应力洛德角对屈服迹线的影响,未考虑到应力洛德角方向的剪切屈服面对土体塑性应变的影响。
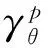
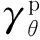
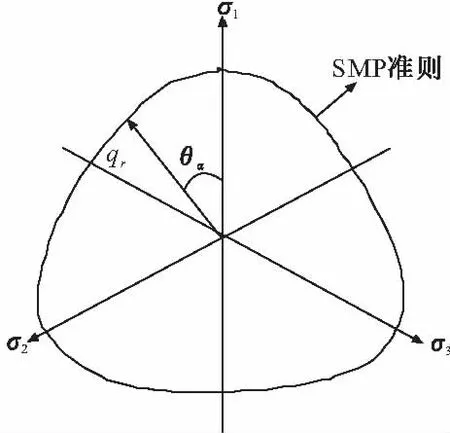
图1 偏平面上的剪切应力分量
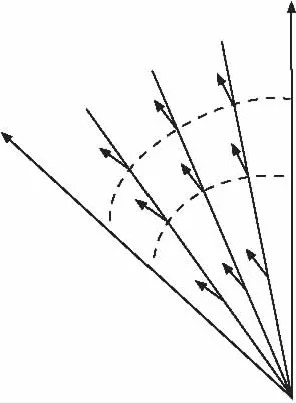
图2 π平面上塑性应变增量方向与屈服轨迹
以上传统弹塑性模型包括单屈服面模型、双屈服面模型、三重屈服面模型,均没有考虑到洛德角θσ方向上剪切屈服面对土体变形的影响。大部分模型是建立在三轴压缩试验的基础上,以平均正应力p和广义剪应力q为变量的屈服方程,然后将模型推广到三维应力条件下,其在π平面的屈服迹线是圆形,没有考虑到应力洛德角对屈服面的影响。
本文提出一个基于广义塑性力学的土体双屈服面本构模型,与传统没有考虑洛德角影响的双屈服面模型相比,此模型充分考虑了洛德角对本构模型的两个方面的影响。通过基于SMP准则的变换应力法或g(θ)方法将模型三维化以考虑不同应力洛德角对屈服迹线的影响,实现偏平面上的剪切分量从三轴压缩到拉伸的变化,同时构建了考虑洛德角θσ方向上塑性剪切应变的屈服面即式(1)中的第三式。该模型“等价”基于广义塑性力学的土体三重屈服面模型,与其相比具有反映土体剪切变形、体积变形且考虑应力洛德角影响的基本相同的特性。
1 模型的建立
1.1 体积屈服面
体积屈服面一般可采用剑桥模型或修正剑桥模型、清华模型。或引入形状参数R的修正剑桥模型:
(3)
式中,R为形状参数;pc为前期固结压力。
这里考虑较简单的情况,选取殷宗泽[14]的压缩屈服面即改进的适用于黏土材料的修正剑桥模型:
(4)

1.2 θσ方向上剪切屈服面
根据广义塑性力学原理,采用的θσ方向上剪切屈服面一般形式可采用式(2),孔亮根据殷宗泽[14]双屈服面模型建议
(5)

(6)
式中,a,b为模型参数,可参考文献 [22],B同式(5)。
1.3 土体的剪胀性反映
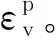
(7)
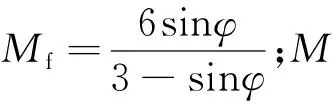
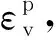
(8)
1.4 本构模型三维化方法
为考虑屈服面函数在π平面的屈服迹线随应力洛德角变化而不同对模型的影响,需对本构模型三维化。直接用广义Mises方法,不会因应力洛德角的不同对土在三维应力状态下的变形和强度产生影响。这里较简单的方法可采用g(θ)方法和姚仰平[23,24]等提出的变换应力方法。
1.4.1变换应力法

(9)
式中,基于SMP准则的
I1,I2,I3为应力不变量;δij为Kronecker符号;
使用变换应力后的三维双曲模型即下式
(10)
三维化后的模型形式与原模型相同,不增加模型参数,可在π平面的屈服面上,实现从剪切屈服到剪切破坏的连续性。
1.4.2g(θ)法
Zienkiewicz-Pand[25]提出了平面上形状函数的方法,g(θ)方法简单。
变换后的三维双曲模型即下式
(11)
这里采用郑颖人等提出的形式来逼近莫尔-库仑不规则六角形
(12)
也可使用其他屈服函数的g(θ),如Zienkiewicz- Pande准则的函数
(13)

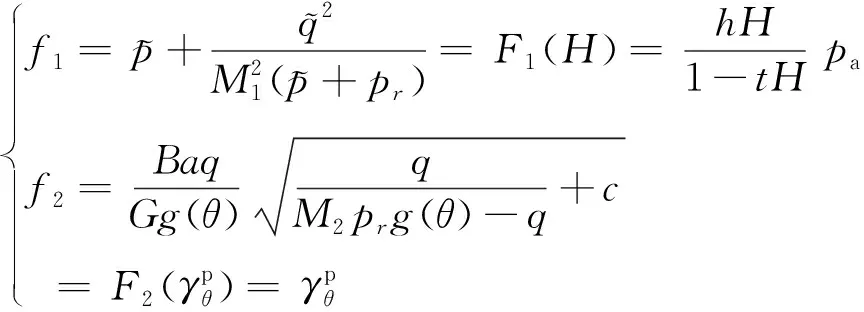
(14)
对于模型式(11)和(14),为简单计,这里采用式(11)模型。此外,因g(θ)方法应用有一定限制,如Zienkiewicz-Pande准则的g(θ)函数中的内摩擦角有限制,不能合理反映应力水平(摩擦发挥角)对变形和强度的影响,对此情况,采用变换应力法能够同时考虑洛德角的影响和应力水平对变形和强度的影响。
2 双屈服面弹塑性模型的应力-应变的刚度矩阵
为便于数值计算,现推导双屈服面本构模型的刚度矩阵。记f1、f2为屈服面,g1、g2为塑性势函数。对如图3双屈模型,将体积屈服面f1两边微分
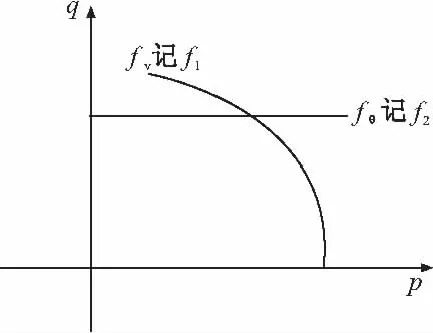
图3 子午平面上的屈服曲线
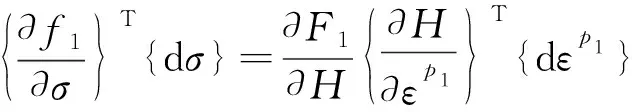
(15)
由相关流动法则
(16)
将式(15)带入式(16),可得
(17)
同理,对于θσ方向上剪切屈服面f2,可得
(18)
其中
对于双屈服面模型的塑性应变增量
(19)
由应力应变关系并带入式(19),可得
{dσ}=[D]{dεe}=[D]({dε}-{dεp})
(20)
将式(20)分别带入式(17)、式(18),可得
(21)
以dλ1、dλ2为未知数解式(21)方程组,可得
(22)
其中
最后将本构方程写成如下形式
{dσ}=[Dep]{dε}
(23)
其中,[Dep]为:
[Dep]=
(24)
至此,推导出了双屈服面本构方程的应力-应变刚度矩阵[Dep], 更便于数值计算分析。
3 结 论
本文提出的一种本构模型本质上是基于广义塑性力学的一个双屈服面模型,具有严格数学推导基础。该模型主要通过四个方面来实现:一是采用传统双屈模型的体积屈服面,较好地反映塑性体积;二是采用传统双屈模型所没有考虑到的θσ方向上剪切屈服面,充分考虑到θσ方向上土体塑性剪切变形;三是在体积屈服面基础上,通过硬化参数的积分变换方法来反映土体的剪胀剪缩特性;四是将本文双屈模型通过g(θ)方法或基于SMP准则的变换应力法模型三维化,考虑到屈服面在偏平面上应力洛德角的影响。
该本构模型可以反映土体的压硬性、剪胀性和摩擦性的基本特性,尤其是充分考虑到了应力洛德角对本构模型的两方面影响即屈服面在偏平面上应力洛德角的影响和θσ方向上土体塑性剪切变形。同时能够反映塑性应变增量方向与应力增量的相关性。可以说该模型在一定程度上与基于广义塑性力学原理的三重屈服面模型是等价的,两者基本具有相同反映土体特性的功能。最后,文中推导给出了双屈本构本构方程的应力-应变刚度矩阵,以便于数值计算。
[1] 沈珠江.关于土力学发展前景的设想[J].岩土工程学报,1994,16 (1):110-111.
[2] Roscoe K H,Schofield A N, Thurairajah A. Yielding of clays in states wetter than critical[J]. Geotechnique, 1963, 13 (3):211-240.
[3] Valanis K C, Fan J H. A numerical algorithm for endochronic plasticity and comparison with experiment[J].Computers and Structures,1984,19(5/6):717-724.
[4] Verdugo R, Ishihara K. The steady state of sandy soils[J].Soils and Foundations,1996, 36 (2):81-91.
[5] Collins I F, Houlsby G T. Application of thermomechnical principles to the modelling of geotechnical materials [J]. Proceedings of the Royal Society A:Mathematical Physical and Engineering Sciences , 1997, 453(1964):1975-2001.
[6] Yao Y P, Sun D A, Matsuoka H. A unified constitutive model for both clay and sand with hardening parameter independent on stress path[J].Computers and Geotechnics, 2008, 35(2):210-222.
[7] Yao Y P,Luo T, Sun D, et al. A simple 3-D constitutive model for both clay and sand[J].Chinese Journal of Geotechnical Engineering, 2002, 24 (2):240-246.
[8] 郑颖人, 孔 亮. 岩土塑性力学M]. 北京:中国建筑工业出版社,2010.
[9] Zhang G Y , Wang J T, Wei J. Study on the numerical method in modeling the constitutive relations of rock and soil [J]. Advances in Systems Science and Applications, 2006, 6 (4):631-636.
[10] Lade P V. Elasto-plastic stress-strain theory for cohesionless soil with curved yield surfaces[J]. International Journal of Solids and Structures, 1977, 13 (11):1019-1035.
[11] Prevost J H, Hoge K. Effective stress-strain strength model for soils[J]. Journal of the Geotechnical Engineering Division, ASCE, 1975, 101 (3):259-278.
[12] Baldi G Y, Rohani B. Elasto-plastic model for saturated sand [J]. Journal of the Geotechnical Eng-ineering Division, ASCE, 1979, 105 (4):465-480.
[13] 沈珠江, 张鲁年.一个计算软土地基固结变形的弹塑性模型[C]//第三届土力学及基础工程学术讨论会论文选集, 杭州, 1979.
[14] 殷宗泽.一个土体的双屈服面应力-应变模型[J].岩土工程学报, 1988, 10 (4):64-71.
[15] 沈珠江.土的三重屈服面应力应变模式[J].固体力学学报, 1984, (2):163-174.
[16] 杨光华, 李广信, 介玉新. 土的本构模型的广义位势理论及其应用[M].北京:水利水电出版社,2007.
[17] 孔 亮, 郑颖人, 王燕昌.一个基于广义塑性力学的土体三屈服面模型[J].岩土力学, 2000, 21(2):108-112.
[18] 张鲁渝,孔 亮, 郑颖人.偏平面上屈服曲线的实验[J].岩土力学, 2002, 23(4):406-410.
[19] 孔 亮, 张鲁渝, 郑颖人.两种土体弹塑性模型三维化方法的比较研究[J].岩土工程学报, 2002, 24 (4):519-521.
[20] 沈珠江.三种硬化理论的比较[J].岩土力学, 1994, 15(2):13-19.
[21] Sun D A, Matsuoka H.Estimate of Initial Modulus of Hyperbolic Stress-strain Relation from Results of Consolidation Tests[C]//Proc. 13th Southeast Asian Geotechnical Conference. Nagoya,1998:171-176.
[22] 陈瑜瑶, 郑颖人. 关于如何确定屈服面的探讨[J].岩石力学与工程学报, 2001, 20(s1):882-885.
[23] Yao Y P, Sun D A. Application of lade’s criterion to cam-clay model [J]. Journal of Engineering Mechanics, 2000, 126(1): 112-119.
[24] Yao Y P, Lu D C, Zhou A, et al. Generalized non-linear strength theory and transformed stress space[J]. Science in China, Series E:Technological Science,2004, 47(6):691-709.
[25] Zienklewicz O C, Pande G N.Some Useful Forms of Isotropic Yield Surface for Soil and Rock Mechanics[C]∥Finite Elements in Geomechanics. London: John Wileye and Sons, 1977:179-190.
