资源约束项目计划内在稳健性与资源使用效率关系

崔万安，汪前珍

(1.广西民族大学 管理学院，广西 南宁 530006；2.广西民族大学 图书馆，广西 南宁 530006)

一、引言

项目计划是项目中的所有活动在满足技术优先关系和资源约束下的一个有序序列，该序列的时间跨度就是项目工期。资源约束项目计划的内在稳健性是指最早项目计划(Left justtified schedule[1]，Minimum duration schedule[2])的项目工期Te对活动工期变化的不敏感性，对这种不敏感性用某种度量指标测度，作为内在稳健性的值。

项目计划工期和项目计划的内在稳健性都是项目管理追求的重要目标，项目工期越短意味着占有资源的时间越短，项目可以更早地交付使用产生效益，项目的投入产出率就越高。众多的学者研究了资源约束项目计划的工期优化问题[3-7]，项目计划的内在稳健性越高，项目执行过程中的不确定因素对项目计划的影响就越小，项目计划按期完成的概率就越高。资源是制定项目计划的重要约束条件，资源使用效率反映了资源在被占有的时段内的利用情况，研究资源使用效率和项目计划内在稳健性的关系，可为制定内在稳健性较高的项目计划提供方法和依据。

Van De Vonder等[2]研究了项目工期与稳定性之间的均衡问题，但没有说明如何建立资源链接，如何确定最晚项目计划(right-justified schedule)，不能保证活动时差的正确性。AL-Fawzan 与Haouari[8]以项目中所有活动的自由时差之和作为稳健性的度量指标，建立了以项目工期和稳健性为优化目标函数的双目标优化模型，Abbasi 等[9]研究了它的有效求解算法。

Kobylański与 Kuchta[10]的研究表明，AL-Fawzan 与Haouari[8]方法未必能达到制定稳健性项目计划的目的。因此，Kobylański与 Kuchta[10]提出用项目中活动自由时差与工期比例的最小值(或活动自由时差的最小值)作为度量稳健性的指标，在一个既定工期T的约束下，求解稳健性最大的项目计划。该度量方法在一定程度上达到了制定稳健性项目计划的目的，缺陷在于：T值如何确定尚无有效方法；该优化模型为二次优化的NP难问题，需要有效的求解算法；若T值等于资源约束项目计划最短工期时，那么制定的稳健性项目计划的稳健性指标值都为零，等价于资源约束项目计划。

Chtourou与Haouari[11]从内在稳健性角度提出了12种内在稳健性的度量指标，但对指标中的总时差计算采用前向(逆向)追溯法[5，12]，没有在项目计划中建立资源链接，因此可能出现假时差[13]。

崔万安等研究了关键序列与项目计划稳健性的关系[14]、项目计划稳健性度量方法[15]，以及资源约束项目计划内在稳健性影响因素[16]。

综上所述，前人研究了项目工期与项目计划稳健性的关系、关键序列与内在稳健性关系、内在稳健性度量等，尚未发现资源使用效率与内在稳健性关系的研究。

二、资源使用效率的定义

资源使用效率的直观含义是在资源被占有时段内，资源使用的时间和使用的数量。如图1，在时刻t=0至时刻t=6的时段内，资源占有的时间为6个单位，在该时段最大可获得资源量为8个单位，即占有资源量为8个单位，所有的资源都得到使用；然而，若项目计划制定在时刻t=0至时刻t=7的时段内，资源占有的时间为7个单位，显然，在其中的一个单位时间内，所占有的8个单位的资源未得到使用；可见，资源使用效率与资源使用时间及使用数量、资源的占有时间及占有数量有关，所以，可以用这四者的关系定义资源的使用效率。项目工期T一旦确定，则在t=0至t=T的时段内，所有的资源都被占有，但资源的使用量取决于活动的工期和活动所需的资源量，因此，可以用资源的使用量和资源的占有量的比率来度量资源的使用效率。资源的使用量(Utilized resource，U)和资源的占有量(Occupied resource，O)定义为：

资源k的占有量Ok=T×Rk.

其中，di表示活动i的工期，rik表示活动i所需第k种的资源量，Rk表示第k种的资源的最大可获得量。显然，Uk与Ok的比值越高，资源空闲的时间就越少，资源使用效率就越高，故可用这二者的比值度量资源k的使用效率。由于项目可能受多种资源的约束，当一种资源的使用效率为100%时，其他资源的使用效率就不可能再提高了。如图1所示，纵轴表示资源的量，横轴表示时间，矩形表示活动，A1、A2、A3、A4、A5为活动编号，显然，在每一时刻，所有的资源都被使用，没有资源空闲，在这种情况下，项目工期不可能通过优化排序的方法来缩短，项目计划的资源使用效率取决于Uk与Ok比值最大的一种资源(即资源使用效率最大的一种资源)，因此，一个项目计划的资源使用效率(Resource Utilization Efficiency，E)定义为：

图1 资源约束项目计划示例

定理：若项目计划P的资源使用效率为100%，则P的项目工期T必为最短的项目工期。

证明：反证法。

由资源使用效率公式，对任意资源k、Uk、Rk是恒量，因此，E仅与项目工期T有关，显然，T越大，资源使用效率越低；T越小，资源使用效率越高。

若项目计划P的资源使用效率为100%，而P不是项目工期最短的项目计划，则必存在一个项目工期最短的项目计划，其项目工期为Tmin，因而有：

显然，若E<1，说明项目计划的资源使用效率还有可能提高，但若项目计划工期已经最短，即便是E<1，资源使用效率也不能再提高了。

三、基本思路

直觉上看，项目工期优化的目的在于尽可能提高资源使用效率，即在t时刻尽可能地使可获得的资源全部得到利用，从而达到缩短项目工期的目的。如图1，在任意时刻最大可获得资源为8个单位，若每一时刻的可获得资源得到完全使用，那么可以得到一个工期最短的项目计划，项目工期为6个单位；反之，若任一时刻有资源剩余，项目工期都将超过6个单位。在图1所示项目计划中，任意一个活动工期的延长都将导致项目计划工期延长，因此，该项目计划的内在稳健性很低。可见，资源使用效率与项目计划内在稳健性之间存在一定的相关性，查明二者之间的关系，可为制定稳健性高的项目计划提供方法和依据。

在此，应用16种优先规则LFT、LST、MaxCRR、MaxCSuc、MaxDur、MaxRPW、MaxRR、MaxSlk、MaxSuc、MinCRR、MinCSuc、MinDur、MinRPW、MinRR、MinSlk、MinSuc[11]对Kolisch设计的j30算例(共480个项目)[17]制定项目计划，计算这些项目计划的资源使用效率，通过仿真实验，得到每个项目计划的内在稳健性的仿真值，计算资源使用效率与内在稳健性的仿真值之间的相关系数并进行假设检验。

四、仿真实验

按照上述基本思路，应用MATLAB7.0编程设计了仿真实验，步骤如下：

1.应用16种优先规则[11]对Kolisch[17]设计的j30算例制定项目计划；

2.计算每个项目计划的资源使用效率E；

3.通过仿真实验得到每个项目计划的内在稳健性值I并进行归一化：随机选取20%活动将之工期延长10%，每个项目计划仿真100次；

4.计算内在稳健性与资源使用效率之间的相关系数c；

5.假设检验(相关系数检验)：比较每种优先规则制定的项目计划在相关系数上的差异。

H0：ρ=0，内在稳健性与资源使用效率无关；

H1：ρ≠0，内在稳健性与资源使用效率相关

在此使用t检验统计量[18]：

其中，显著性水平取0.005，t0.005=2.586.

ρ：内在稳健性与资源使用效率的总体相关系数；c：内在稳健性与资源使用效率的样本相关系数；n：算例的数量，n=480.

五、实验结果分析

对于16种优先规则制定的项目计划，通过仿真实验得到各个项目计划的内在稳健性的仿真值和资源使用效率，假设检验结果表明(见表1)，对于每种优先规则制定的项目计划，内在稳健性和资源使用效率之间存在显著的负相关关系，实验验证了提高资源使用效率将降低项目计划的内在稳健性，与直觉一致。

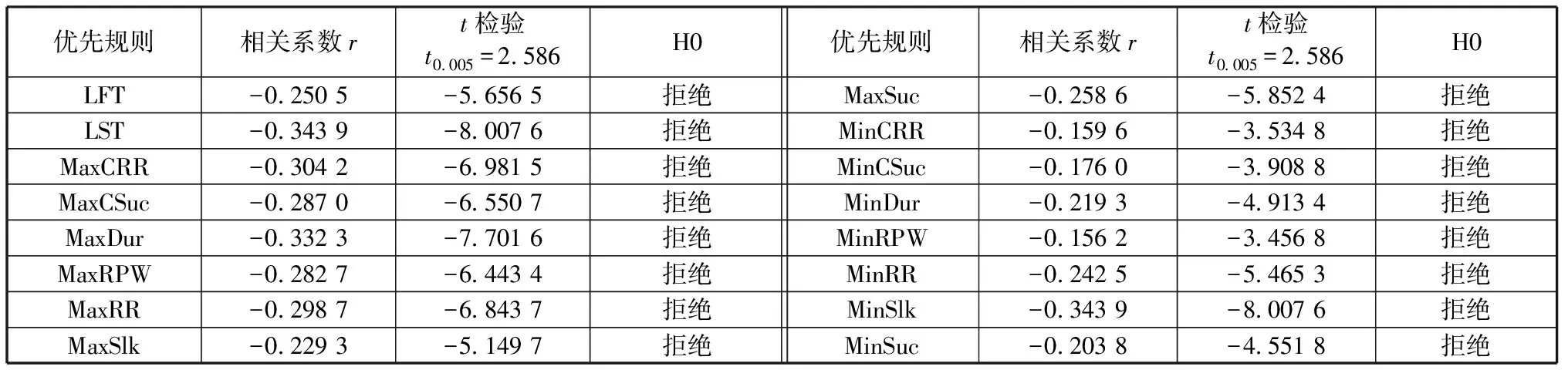
表1 假设检验结果(j30)

六、结论

资源约束项目计划的内在稳健性受多种因素的影响，查明这些因素与内在稳健性的关系，可为稳健性项目计划的制定和预测提供依据。本文严格定义了资源使用效率，应用16种优先规则对Kolisch的j30算例集中的480个算例制定项目计划，并计算出各项目计划的资源使用效率，通过仿真的方法得到各项目计划的内在稳健性值；实验结果表明，项目计划的内在稳健性与资源使用效率之间存在显著的负相关关系，即资源使用效率越高，项目计划的内在稳健性越低，这与直觉一致。下一步将研究项目计划内在稳健性与各影响因素之间的回归方程，以期通过各影响因素的变化预测内在稳健性的变化。

参考文献：

[1] Wiest J.D.Some properties of schedules for large projects with limited resources[J].Operations Research，1964，12(3)：395-418.

[2] Stijn Van de Vonder，Erik Demeulemeester，Willy Herroelen and Roel Leus.The trade-off between stability and makespan in resource-constrained project scheduling[J].International Journal of Production Research，2006，44(2)：215-236.

[3] Herroelen，Willy；De Reyck，Bert；Demeulemeester，Erik，Resource-constrained project scheduling：A survey of recent developments[J].Computers and Operations Research，1998，25(4)：279-302.

[4] Brucker，Peter；Drexl，Andreas；Möhring，Rolf；Neumann，Klaus；Pesch，Erwin；Resource-constrained project scheduling：Notation，classification，models，and methods[J].European Journal of Operational Research，1999，112(1)：3-41.

[5] Hartmann，Sönke and Kolisch，Rainer，Experimental evaluation of state-of-the-art heuristics for resource constrained project scheduling[J].European Journal for Operational Research，2000(127)：394-407.

[6] Kolisch，R and Padman，R，An integrated survey of deterministic project scheduling[J].Omega，2001，29(3)：249-272.

[7] Herroelen，Willy；Demeulemeester，Erik；De Reyck，Bert，A note on the paper “Resource-constrained project scheduling：Notation，classification，models and methods” by Brucker et al[J].European Journal of Operational Research，2001，128(3)：679-688.

[8] M.A.Al-Fawzan and Mohamed Haouari.A bi-objective model for robust resource-constrained project scheduling[J].International Journal of Production Economics，2005，96(2)：175-187.

[9] Babak Abbasi，Shahram Shadrokh and Jamal Arkat.Bi-objective resource-constrained project scheduling with robustness and makespan criteria[J].Applied Mathematics and Computation，2006，180(1)：146-152.

[11] Hédi Chtourou，Mohamed Haouari A two-stage-priority-rule-based algorithm for robust resource-constrained project scheduling[J].Computers & Industrial Engineering，2008，55(1)：183-194.

[12] K.Y.Li，R.J.Willis，An iterative scheduling technique for resource-constrained project scheduling[J].European Journal of Operational Research，1992，56(3)：370-379.

[13] Kim K.，De la Garza J.M，Phantom float[J].Journal of Construction Engineering and Management，2003，129(5)：507-517.

[14] 崔万安，王先甲.资源约束项目计划关键序列与内在稳健性关系研究[J].水电能源科学，2010，28(7)：127-129.

[15] 崔万安，王先甲.资源约束项目计划内在稳健性度量方法[J].水电能源科学，2010，28(8)：123-125.

[16] 崔万安，王先甲.资源约束项目计划内在稳健性影响因素分析[J].太原理工大学学报：社会科学版，2010，28(1)：20-23.

[17] Kolisch R.，Sprecher A.，PSPLIB-A project scheduling problem library[J].European Journal of Operational Research，1997，96(1)：205-216.

[18] 张原粲，徐建平.现代心理与教育统计学[M].北京：北京师范大学出版社，2003.