图书馆流通借阅系统的建模与仿真*

杨红军

(长春工业大学 图书馆，吉林 长春130012)

1 问题描述

图1，我们以单服务台队列系统为例，假设读者(实体)到达间隔时间为A1,A2,…,并且是相互独立的同分布的随机变量(同分布是指到达时间间隔具有相同的概率分布).一个读者到达，发现服务台空闲，就可以立即接受借阅服务，读者的服务时间S1,S2,…,是独立同分布的随机变量，而且与到达间隔时间相互独立.如果读者到达发现服务台繁忙，就只能到队列最后排队等待.当服务完成后，服务台就会从队列中选择下一个读者为其提供服务，排队规则是FIFO.[1]

图1 单服务台排队系统

仿真模型初始化状态：在时间0时刻，系统中没有读者，服务台处于空闲状态.第一个读者在A1时刻到达.仿真结束条件是第n个读者结束他的排队等待，开始接受服务.仿真系统结束的时间是一个随机变量，取决于到达间隔时间的观察值和服务时间的随机变量.[2]

系统的事件包括读者到达、读者离开；用于评价系统性能的指标是读者平均等待时间d(n)、排队长度q(n)和服务台的利用率u(n)；描述服务状态的变量是服务台状态B(t)(空闲是0，繁忙是1)、排队人数Q(t)、读者到达队列的时间，状态变量变化都发生在事件时间.[3]

图2 单服务台排队系统的Q(t)、到达时间、离去时间

T0=(1.6-0.0)+(4.0-3.1)+(5.6-4.9)=3.2

T1=(2.1-1.6)+(3.1-2.4)+(4.9-4.0)+(5.8-5.6)=2.3

T2=(2.4-2.1)+(7.2-5.8)=1.7

T3=(8.6-7.2)=1.4

(当i≥4时，Ti=0，是说明在现实情况下，队列不会无限增加.)

于是Q(t)随时间变化的曲线下的面积可以写成：

(1)[5]

2 数据分析

q(n)的估计值是

(2)

式(2)是Q(t)的连续时间平均值.[6]

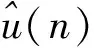
(3)

图3 单服务台排队系统的B(t)、到达时间、离去时间

这说明在仿真过程中，服务台的繁忙率是90%.而且式(3)中的分子是B(t)函数曲线下对应的面积，而B(t)的高度只有两个取值：0和1.所以，

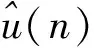
延误是离散统计变量，因为它与随机变量集合{Di}相关，该集合时间指标是离散的，i=1，2，….队列中的平均排队长度和服务台的利用率都是连续时间统计量，二者分别与随机变量Q(t)和B(t)相关，Q(t)和B(t)都是连续时间的函数，其中t∈[0，∞).离散时间和连续时间统计量在仿真中很常见，而且不仅仅可以求平均值.例如，我们可能需要队列等待的最大延误时间(离散时间统计量)，或者队列人数至少是5人的时间占仿真时间的比例(连续时间统计量).[10]

3 结论

上述系统性能指标的计算方式能够有效地节约各种公共资源，提高服务效率，减少排队时间，从而达到既方便读者又提高了图书管理人员功效的目的.

参考文献：

[1]Averill M.Law.仿真建模与分析[M].第四版.北京：清华大学出版社，2009:126-127.

[2]蔡建峰.管理系统模拟[M].北京：机械工业出版社，2007:189-190.

[3]范文慧，肖田元，译.离散事件系统仿真[M].原书第4版.北京：机械工业出版社，2007:107-111.

[4]顾启泰.离散事件系统建模与仿真[M].北京：清华大学出版社，1999:152.

[5]黎志成，等.管理系统模拟[M].北京：清华大学出版社，1989:217-218.

[6]孙铮.管理系统模拟[M].哈尔滨：哈尔滨工业大学，1996，99-100.

[7]王维平.离散事件系统建模与仿真[M].第二版.北京：科学出版社，2007:311-312.

[8]王维平，等.仿真模型有效性确认与验证[M].北京：国防科技大学出版社，1998:101-103.

[9]王子才.仿真技术发展及应用[J].中国工程科学，2003(2):40-41.

[10]卫强，陈国青.管理系统模拟[M].北京：高等教育出版社，2008:66.