自回归聚合风险模型*

王丙参，张凡弟，田玉柱

(天水师范学院 数学与统计学院，甘肃 天水 741001)

1 问题的表述及模型的建立

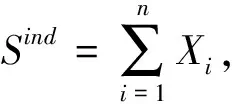
(1)给定时间内的短期集合风险模型

(2)长期聚合风险模型

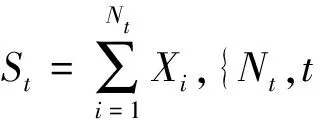
模型(1)考虑的仅是一个固定时间内的理赔次数和总理赔量.模型(2)讨论的是对∀t≥0时的概率结构及其应用[5].

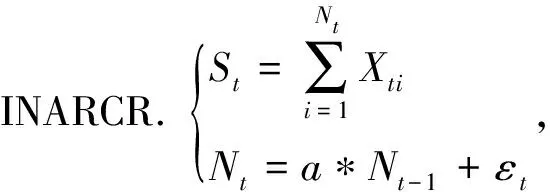
2 基本性质

定理1 在长期聚合风险模型中有

mgfmst(x)=mNt(logmXi(x))，
E[St]=E[Xi]E[Nt]
Var(St)=E[Nt]Var[Xi]+(E[Xi])2Var[Nt].

证明

mst(x)=E[exSt]=E[E[exSt|Nt]]=
E[Mxi(t)Nt]=mNt(logmXi(x)).

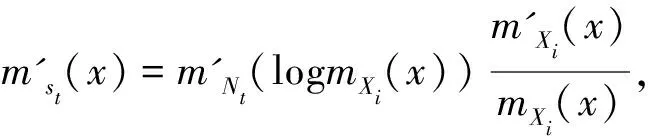
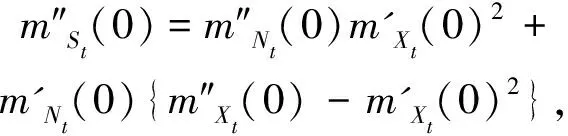
所以，

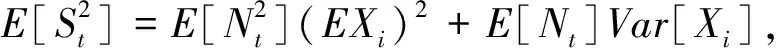
3 风险模型的性质

定理2 在自回归模型中，N0～P(r0)，{εt}是泊松过程，其中εt～P(λt)且λ1<λ2<…<λt<…，则Nt～P(λt+aE(Nt-1))，其中

E(Nt-1)=λt-1+aλt-2+…+d-1r0.

证明

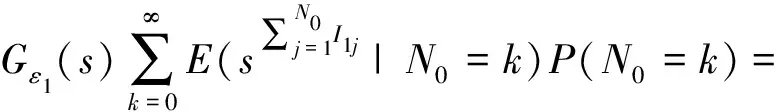
所以N1～P(λ1+ar0)，由数学归纳法可证对∀t∈{0，1，2，…}，Nt～P(λt+aE(Nt-1)).

定理3 设Nt～P(rt)，Xt1，Xt2，…，i.i.d，且与{Nt}独立，则(1)φst(x)=exp{rt[φXt1(x)-1]}；(2)若E(Xt1)<∞，则E(St)=rtE(Xt1)，

证明

exp{rt[φXt1(x)-1]}

(2)证法1

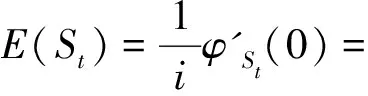
证法2

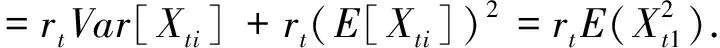
特别有推论:

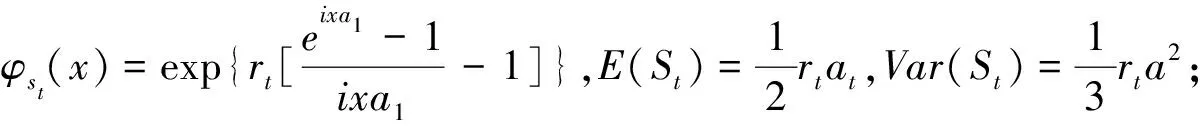
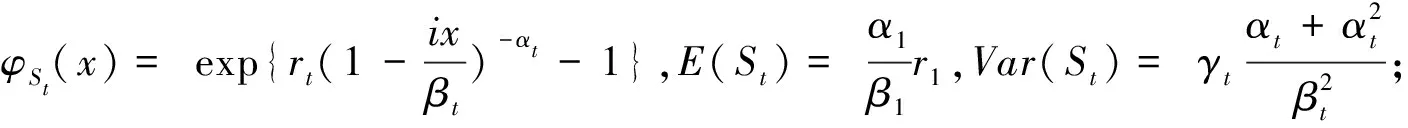
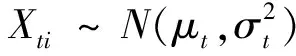
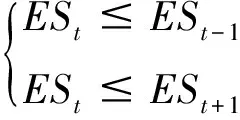
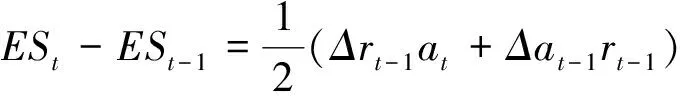
在推论(1)的条件下，当

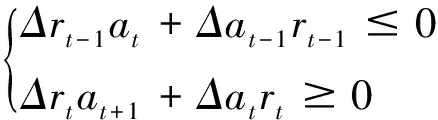
ESt在t时达到相对极小值；

同理可得，在推论(2)的条件下，当

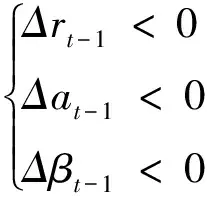
ESt在t时达到相对极小值；

在推论(3)的条件下，当

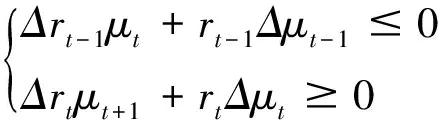
ESt在t时达到相对极小值.

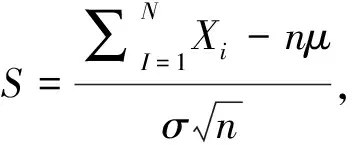
这样有

如果n足够大，则上面近似可以放心地使用，但我们很难对足够大定义一个标准.

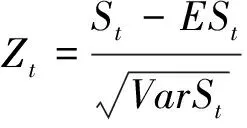
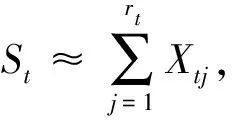
在某些情形下我们不得不求助于一些近似公式，尤其在实际计算时间过长的时候.随着rt的增大近似的效果会改善，它们是渐进精确的，这是因为在极限意义下它们同基于中心极限定理的正态逼近.但这种近似在保险实际中不能令人满意，尾概率的近似误差偏大，转化为数学语言就是st的三阶中心矩通常大于0，而正态分布的三阶中心矩等于0，而尾概率对应于大额理赔的概率，因此我们需要更为精细的近似.

参考文献：

[1]周俊士，成世学，程乾生.个体风险模型的复合possion模型近似[J].运筹学学报，2003，7(2).

[2]R.卡尔斯，等.现代精算风险理论[M].唐启鹤，等译.北京:科学出版社，2005(3).

[3]李贤德，杨静平.个体风险模型的复合Poisson逼近[J].北京大学学报:自然科学版，2001，37(5).

[4]施久玉.一类聚合风险模型[J].运筹与管理，2004，16(6).

[5]施久玉.整值自回归聚合风险模型-INARCR[J].哈尔滨工程大学学报，2004，25(3).