Fuzzy traffic signal control with DNA evolutionary algorithm

Bi Yunrui Lu Xiaobo Sun Zhe Zeng Weili

(1School of Automation,Southeast University,Nanjing 210096,China)

(2Institute of Cyber-Systems and Control, Zhejiang University, Hangzhou 310027, China)

(3School of Transportation,Southeast University,Nanjing 210096, China)

Traffic signal control has attracted considerable interest because road traffic congestion is a critical problem. The fuzzy logic theory has played an important role in adaptive traffic signal control in recent years. Pappis et al.[1]first proposed an implementation of a fuzzy logic controller (FLC) in a single intersection of two one-way streets in 1977. Trabia et al.[2]developed a fuzzy logic controller for an isolated four-approach signalized intersection which mainly determines whether to extend or terminate the current signal phase. Murat and Gedizlioglu[3]developed a fuzzy logic multi-phased signal control model for isolated signalized intersections. In addition, the use of the optimized method has demonstrated its usefulness in traffic signal distribution strategy. Srinivasan[4]presented a real-time traffic signal control method based on neural networks. Anderson et al.[5]proposed a GA-optimized fuzzy logic controller traffic signal control. Garcia-Nieto et al.[6]utilized the particle swarm optimization (PSO) method for traffic light scheduling. Dimitriou et al.[7]presented an adaptive hybrid fuzzy rule-based system (FRBS) approach.

However, the DNA evolutionary algorithm can overcome the drawbacks of the GA, such as weak local search capability and premature convergence[8-9]. In this paper, we propose a fuzzy logic controller for traffic signal control and utilize the GA and the DNA evolutionary algorithm to optimize FLC membership function parameters, respectively. Then the optimized FLC is applied to traffic signal control.

1 Fuzzy Logic Controller for Signal Control

In this paper, we consider a single traffic junction with multiple lanes. The number of street lanes ranges from 1 to 3, as shown in Fig.1.

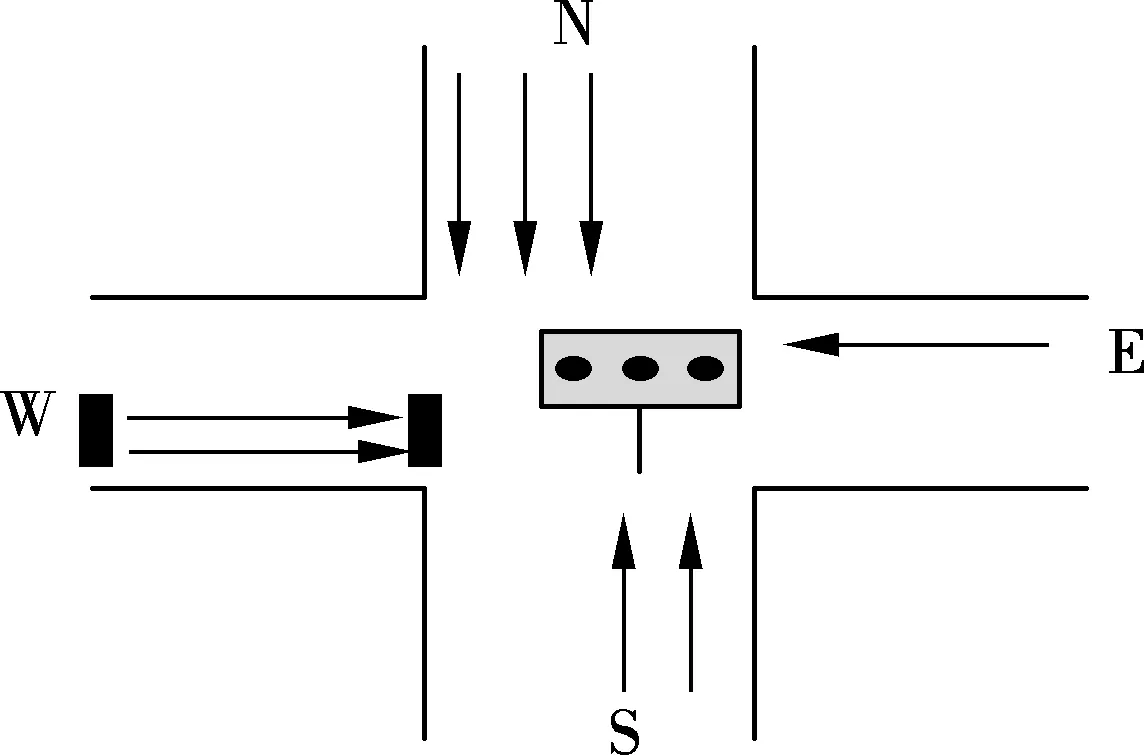
Fig.1 A single traffic junction with multiple lane

As shown in Fig.1, each group of traffic loop detectors consists of two sensors, one at the downstream stop line for recording the departure vehicles and the other at the corresponding intersection upstream for estimating the arriving vehicles. For multiple lanes, drivers tend to switch to a shorter queue while approaching the junction, so the differences among queue lengths of all the lanes in the same direction are usually small. If the north-south direction is in the green phase, then we can let

G=max {queue lengths of all lanes in north and

south directions}

R=max {queue lengths of all lanes in east and

west directions}

At the beginning of every phase,GandRare measured, which are the two input variables of the fuzzy logic controller. We select the green time of the current phaseTas output variable. Without loss of generality, we adopt the same Gaussian membership function of which the universe of discourse is (0, 12).

All these variables are divided into seven fuzzy language partitions: very short(VS), medium short(MS), short(S), medium(M), long(L), medium long(ML), and very long(VL). The rule base is shown in Tab.1.

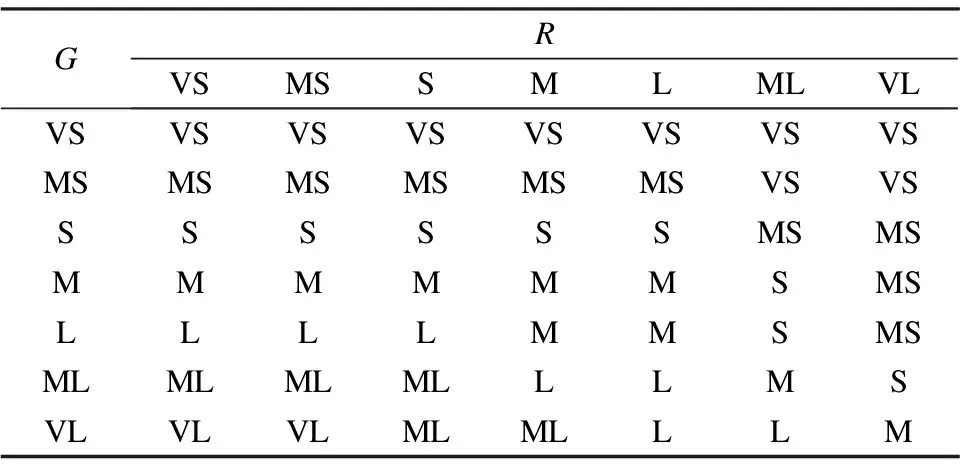
Tab．1 Fuzzy inference rule base

2 OptimizationProcesswithDNAEvolutionaryAlgorithm

2.1 DNAevolutionaryalgorithmandencodingprinciple

The DNA evolutionary algorithm adopts the characteristics of the DNA model, which encodes chromosomes and amends genetic operators with the DNA nucleotide mechanism. The DNA algorithm has several kinds of operators as follows:

1) Selection operator. Elitism is used with tournament selection in attempt to guarantee the best individual to be replicated into the next generation.

2) Translocation operator. This operator makes the subsequence of the DNA sequence transfer to a new location. For example, let the original DNA sequence beX=X5X4X3X2X1, whereXi(i=1,2,…,5) is the subsequence of the DNA sequence (X). Then the new sequence after the translocation operation becomesX=X5X2X4X3X1.

3) Transformation operator. This operator makes the segments of the DNA sequence exchange their locations. For example, the sequenceXafter a transformation operation which exchangesX4withX2becomesX=X5X2X3X4X1.

5) Mutation operator. In order to maintain the population diversity, we employ the shifty probability in different evolution stages. At the beginning of the evolution stage, we want to have a large probability in the high bit position so as to obtain a large searching space. At the end of the evolution stage, the large probability in the low bit position is necessary for acquiring more accurate results. So there are two kinds of mutation probabilityPhandPl,

(1)

(2)

wherea1,b1,g,g0andadenote the initial mutation probability, the range of the mutation probability, the evolutionary generation, the generation where the great change of mutation probability occurs, and the speed of change, respectively.

2.2 Procedure of DNA genetic algorithm

On the basis of the DNA encoding principle and corresponding genetic operators, for the Gaussian membership function, two input variables and one output variable are encoded in a 42 real gens chromosome by using the quaternary encoding method. The procedure of the DNA genetic algorithm is as follows:

Step1Initialize populationNand evolutionary generationGenand encode the individuals using the DNA encoding method.

Step2Set the fitness function and calculate the individuals’ fitness values.

Step3Implement the selection operator with elitism from the population so as to select the individuals of high value and reproduce similar individuals.

Step4Utilize the permutation operator and set the random number with the range of [0, 1]. If the random numberi>pc=0.5, implement the translocation operator, otherwise implement the transformation operator.

Step5CalculatePh,Pland implement the mutator operator. On the basis of the Watson-Crick complementary principle, produceNcorresponding complementary individuals after the mutation operation. Then the population is enlarged with 2Nindividuals.

Step6If the criterion is met or the loop of the evolutionary process is completed, end this algorithm. Otherwise, repeat from step 2 to step 6 until the final optimized solutions are found.

3 Simulation

3.1 Queuelengthandaveragedelaymodel

In order to illustrate the validity of the methods for traffic signal control, the intersection queue lengths and the average delays are usually selected as criteria. In this model, assume that the arrival time of vehicles is random. In each successive time unit (1 s), if a vehicle arrives during then-th unit interval, letqn=1. Otherwise, letqn=0.VGdenotes the number of vehicles that cannot leave during the previous green phase.VRdenotes the number of vehicles that arrive during the red phase. Then the queue lengths of the red phase and the green phase after then-th time unitQR,QGare depicted as

(3)

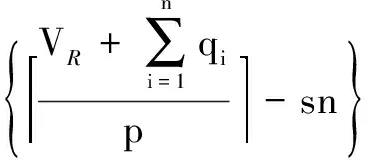
(4)

The total delay time of the vehicles at the red phase of this cycle is

(5)

Then the total waiting time at the green phase of this cycle can be described as

(6)

Therefore, during thel-th cycle the total delay time experienced by vehicles and the average delay time are

(7)

(8)

whereglandrlare the numbers of vehicles that arrive at the green phase and the red phase in thel-th cycle, respectively;gl-1andrl-1are the numbers of vehicles that stay at the green phase and the red phase in the previous cycle, respectively.

3.2 Simulation results

According to the queue length and the average delay model, simulation experiments are constructed by varying the arrival rates of vehicles. Different control methods are compared, which include the fixed-time control, the FLC that does not use any optimization technique, the GA optimized FLC (GA_FLC), and the FLC with DNA optimization(DNA_FLC). Simulation results are shown in Tab.2 and Fig.2.

From Tab.2, we can see that the delay time of FLC with the DNA genetic algorithm optimization is significantly shortened compared with the other methods at different vehicle arrival rates. Especially, when the arrival rate of vehicles is high, the difference of these methods is bigger. Fig.2 compares the total queue length for different arrival rates of vehicles given by different methods. Especially, from Fig.2(b) we can see that when the traffic becomes heavy, the method with the DNA optimization can let vehicles evacuate instead of gathering in other methods. It illustrates that the FLC with the DNA genetic algorithm optimization shows more superiority when traffic flow is heavy.

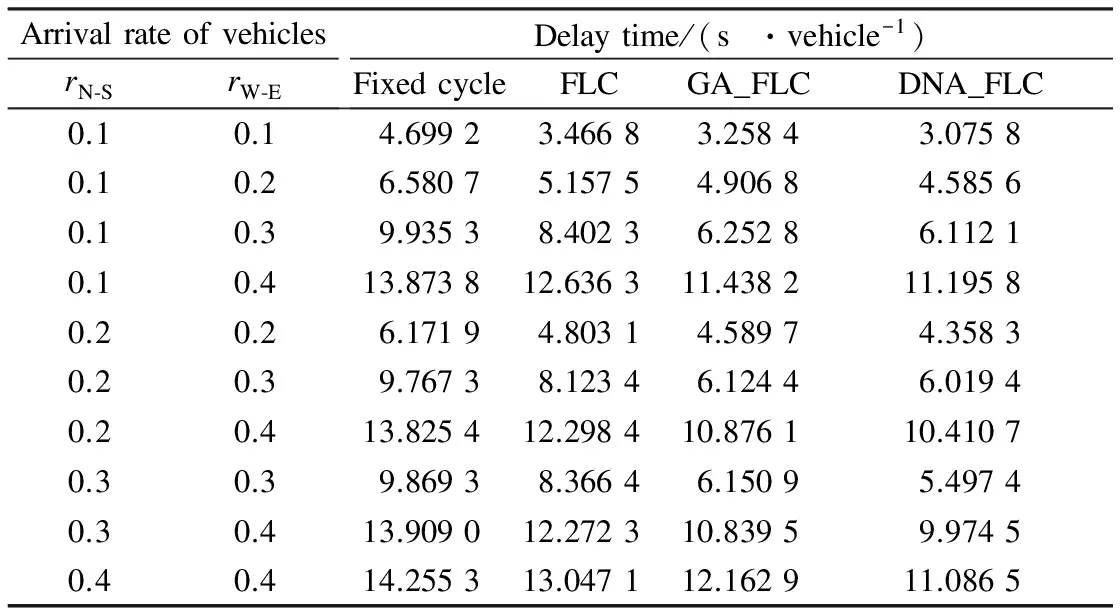
Tab．2 Results of simulation

Fig.2 Queue length in different arrival rates under four methods. (a) rN-S=0.2,rW-E=0.2; (b) rN-S=0.3,rW-E=0.3; (c) rN-S=0.3,rW-E=0.4; (d) rN-S=0.4,rW-E=0.4

4 Conclusion

In this paper, we design a fuzzy logic controller based on the DNA evolutionary algorithm and apply the optimized fuzzy logic controller to simulate single intersection signal control. The DNA evolutionary algorithm inherits the advantages of the GA and adds DNA molecular operation characteristics. It presents better searching capability and maintains diversity of the population. Compared with the fixed-time controller, the traditional fuzzy logic controller and the fuzzy logic controller optimized by the GA, the proposed fuzzy logic controller shows better performance in the distribution of green/red time.

[1]Pappis C, Mamdani E. A fuzzy logic controller for a traffic junction [J].IEEETransactionsonSystems,ManandCybernetics, 1977,7(10): 707-717.

[2]Trabia M B, Kaseko M S, Ande M. A two-stage fuzzy logic controller for traffic signals [J].TransportationResearchPartC, 1999,7(6): 353-367.

[3]Murat Y S, Gedizlioglu E. A fuzzy logic multi-phased signal control model for isolated junctions [J].TransportationResearchPartC, 2005,13(1): 19-36.

[4]Srinivasan D, Choy M C, Cheu R L. Neural networks for real-time traffic signal control [J].IEEETransactionsonIntelligentTransportationSystems, 2006,7(3): 261-272.

[5]Anderson J J, Sayers T M, Bell M G H. Optimizations of a fuzzy logic traffic signal controller by a multiobjective genetic algorithm [C]//Proceedingsofthe9thInternationalConferenceonRoadTransportInformationandControl. London, UK, 1998:186-190.

[6]Garcia-Nieto J, Alba E, Olivera A C. Swarm intelligence for traffic light scheduling: application to real urban areas [J].EngineeringApplicationsofArtificialIntelligence, 2012,25(2): 274-283.

[7]Dimitriou L, Tsekeris T, Stathopoulos A. Adaptive hybrid fuzzy rule-based system approach for modeling and predicting urban traffic flow [J].TransportationResearchPartC, 2008,16(5): 554-573.

[8]Chen X, Wang N. A DNA based genetic algorithm for parameter estimation in the hydrogenation reaction [J].ChemicalEngineeringJournal, 2009,150(2/3): 527-535.

[9]Chen X, Wang N. Optimization of short-time gasoline blending scheduling problem with a DNA based hybrid genetic algorithm [J].ChemicalEngineeringandProcessing:ProcessIntensification, 2010,49(10): 1076-1083.