Aggregating metasearch engine results based on maximal entropy OWA operator

Sang Xiuzhi Liu Xinwang

(School of Economics and Management, Southeast University, Nanjing 211189, China)

In recent years, the world wide web (WWW) has been a main place to find information about any area. It has become the most frequently used tool for locating specific information. However, several attempts have been reported that the results being searched for with the same query in different search engines differentiate significantly at the same time[1-2]. But what users want is to find accurate information through employing a general-purpose search engine in a timely and cost-effective way, which seems to be unrealistic[1,3]. Therefore, aggregating the retrieval results from different search engines can significantly improve the quality of final metasearch engine results[4]. A metasearch engine is a system that supports unified access to multiple existing search engines[5-6].

Diaz et al.[1]demonstrated that the metasearch engine provides a significant improvement in coverage of search effectiveness. Dreilinger and Howe[7]adopted a pragmatic approach to the problem of information retrieval on the web. A comprehensive survey for building an efficient metasearch engine was provided by Meng et al[8]. Keyhanipour et al.[4]used the optimistic OWA operator to aggregate metasearch engine results. Emrouznejad[2]proposed the most preferred OWA operator to aggregate search engine results. Herrera-Viedma et al.[9]analyzed the role of aggregation operators to access information on the web. Amin and Emrouznejad[5]proposed the minimax linear programming model for aggregating multiple search engine results. Diaz et al.[10]proposed a fuzzy analytic network process (ANP) and weighted fuzzy ANP methods for merging metasearch engine results. To the best of the author’s knowledge, no single research is reported to find the metasearch engine results of a specific query using the crisp OWA operator weights.

There are some other kinds of OWA operator weights determining methods[11-15]. This paper proposes a new application of the ME-OWA operator method for aggregating metasearch engine results obtained from a specific query. Three reasons contribute to our decision for using the ME-OWA operator. First, it is simple, comprehensible and convenient for users to know. Secondly, the weights obtained by the ME-OWA operator change monotonically and smoothly with the position index, which can well reflect the importance of the retrieval documents in different positions[12]. Thirdly, if we use other OWA operator methods, the frameworks of finding metasearch engine results are the same.

This paper first gives a general approach to finding metasearch engine results. Then it divides the existing OWA operator methods into two kinds: one is to acquire unique aggregation results, the other is to acquire multiple aggregation results. But the existing solutions to the second kind are fuzzy search engine weighted approaches. Whereas, aggregating metasearch engine results is a crisp problem, we should use crisp weights to aggregate the metasearch engine results. The ME-OWA operator not only provides crisp weights, but also has multiple aggregation results for decision makers to choose from. Meanwhile, we elaborate on the advantages of the proposed method. In the end, an example is provided to illustrate its application, which extends the aggregation results of the minimax-LP method[5].

1 ExistingMethodsforAggregatingMetasearchEngineResults

As is stated above, we just discuss the problem of aggregating metasearch engine results in the OWA operator context.

1.1 Ageneralapproachtoaggregatemetasearchenginesresults

The OWA operator aggregation process can be divided into two phases:

1) Aggregating phase. Submit queries to the metasearch engine system, which dispatches them to the selected search engines; then each search engine extracts a retrieval list. Count the frequencyλijof documentDiappearing in thej-th place and compute the weighting vectorsWwith the relevant OWA operator method; then obtain aggregation values for metasearch engine results.

2) Ranking phase. Order the aggregation results according to a given criterion (i.e., the degree of orness associated with the OWA operator) to obtain the optimal rank.

Let us consider an application of the OWA operator in the metasearch system[2]. Suppose that there are msearch engines (m≥2) denoted by SE1,…, SEm. Without loss of generality, we only consider the firstl-th ranked list of documents retrieved from each search engine. LetD1,…,Drdenote the documents appearing in the retrieval lists. The corresponding data can be recorded in Tab.1.

Tab.1 The appearing place of documents

In Tab.1,λji(j=1,2,…,r;i=1,2,…,l) denotes the frequency of documentDjappearing in thei-th ranked place.

The relevancy index of documentDkis defined as

(1)

wherewi(i=1,2,…,l) is the unknown weight defined for thei-th place. It is noted that the weight should satisfywi≥wi+1because the greater the frequency number, the more relevant to the query, and we should give them more weights.

In Eq.(1), it is obvious that the aggregation valuezkis dependent upon the weighting vector. So, the problem of aggregating metasearch engine results can be changed into obtaining a proper weighting vector under the OWA operator.

Yager[16]was the first introducing the concept of the OWA operator which has the ability to derive optimal results based on the weighting vectors after an aggregation process and it is defined as follows.

Definition1An OWA operator of dimensionnis a mappingFW:Rn→Rthat has weightsW={w1,w2,…,wn}Twith properties as

w1+w2+…+wn=1 0≤wi≤1;i=1,2,…,n

(2)

Such that

(3)

whereyiis thei-th largest value inxi.

Yager[16]also introduced two important measures with respect to the weighting vectorWof problem (3), which are defined as follows.

Definition2[16]Assume thatW={w1,w2,…,wn}Tis the weighting vector of problem (3), the orness level is defined as

(4)

where orness(W)=αandα∈[0,1].

Definition3[16]Assume thatW={w1,w2,…,wn}Tis the weighting vector of problem (3), the dispersion measure is defined as

(5)

1.2 Existingmethodstoaggregatemetasearchengineresults

1.2.1 Method of acquiring unique solution

It means that we can obtain an unique optimal weighting vector by solving a certain method without artificially adjusting any parameters, related researches can be referred to Refs.[2,5]. Here, we just introduce the minimax-LP method[5], because we will compare the ranking with that of the ME-OWA operator.

The minimax-LP method minimizes the maximum deviation from relevancy indices corresponding to the aggregated elements, which can be expressed as

minM

(6)

s.t.M-dj≥0j=1,2,…,r

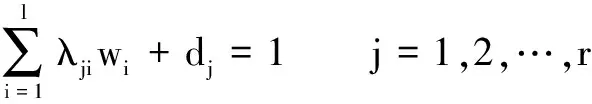
wi-wi+1≥ε*i=1,2,…,l-1

wl≥ε*

dj≥0

whereM=max{dj:j=1,2,…,r};djis a deviation variable;wiis the unknown weight defined for thei-th place;λji(j=1,2,…,r;i=1,2,…,l) is the frequency documentDjappeared in thei-th ranked place;ε*is the maximum discriminating parameter, and the value is obtained as follows:

1.2.2 Method of obtaining multiple solutions

It means that we obtain multiple aggregation results through solving a model with certain predefined parameters to acquire different weighting vectors.

The linguistic quantifier was originally introduced by Zadeh[17]. Later, Yager[18]proposed a fuzzy linguistic regular increasing monotone(RIM) quantifier guided aggregation with the OWA operator, which is defined as follows.

Definition4[18]A fuzzy subsetQis called an RIM quantifier ifQ(0)=0,Q(1)=1, andQ(x)≥Q(y) ifx≥y.

With an RIM quantifierQ, the weighting vector of the OWA operator can be obtained by

(7)

The quantifier guided aggregation with the OWA operator is

(8)

wherexiis in a decreasing order.

The fuzzy linguistic quantifierQgenerally represents the concept of a fuzzy majority in the arguments aggregation[19]. Various applications are discussed in Refs.[1,10].

It is so flexible that decision makers can obtain an optimal solution through multiple aggregation results. But fuzzy linguistic quantifier guided aggregation is used to solve fuzzy decision making problems; it is not suitable for solving crisp decision making problems. In this paper, we introduce the ME-OWA operator method to the application of aggregating metasearch engine retrieval results, which not only has crisp weights, but also has multiple aggregation results for decision makers to choose from.

2 ApplicationofME-OWAOperatorMethodinMetasearchEnvironment

2.1 ME-OWA operator and its computation

O’Hagan[11]combined the principle of the maximum entropy with the OWA operator and proposed the following mathematical programming problem:

(9)

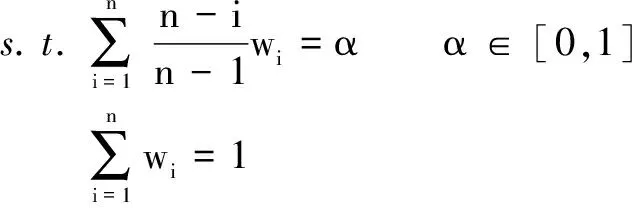
wi≥0i=1,2,…,n

Various optimal solutions were discussed in Refs.[11-12,20]. There is an important property of problem (9), which is expressed as follows.

Theorem1[12]Sinceαis the orness level of problem (9), when 0.5≤α≤1, the weights form a nonincreasing sequence, andwi≥wjfori≤j. When 0≤α≤0.5, the weights form a nondecreasing sequence, andwi≤wjfori≥j.

From Theorem 1, when 0.5≤α≤1, the greater the aggregated element is, the more emphasis will be given; when 0≤α<0.5, the smaller the aggregated element is, the more emphasis will be given.

In the application of aggregating metasearch engine results, the more frequent the document is, the more relevant the query will be. So, we just consider the weights of problem (9) under orness levelα∈[0.5,1].

Using the method of Lagrange multipliers, Liu[21]and Fullér et al.[12]transformed problem (9) into a polynomial equation to determine the optimal weighting vectors. In this paper, we use the analytical solution of Liu’s method[21], which has a geometric form withwi+1/wi=q, and the weightswican be expressed as[21]

(10)

whereqis the root solution to problem (9) that can be solved by

(11)

Various applications of problem (9) are discussed in Refs.[11-12,20].

Next, we will introduce the analytical process of aggregating metasearch engine results.

2.2 Proceduresofaggregatingmetasearchengineresults

We divide the procedure into several steps as follows:

Step1Choose search engine (SE1,…,SEm) in the metasearch environment, and submit a specific query to these search engines.

Step2Determine the firstl-th ranked list.

Step3To each documentDj, count the frequencyλji(j=1,2,…,r;i=1,2,…,l) appearing in thei-th place.

Step4Takenandαinto Eq.(11), and compute the value ofq.

Step5Takeqinto Eq.(10), and compute weighting vectorWwith given ornessα.

Step6According to Eq.(1), calculate the aggregation results of each documentDjwith the given weighting vector.

Step7With respect to the aggregation results, rank the retrieval documentDj.

In the above process, Steps 1 to 6 are aggregating phases, and Step 7 is a ranking phase. Combining the conclusions in Theorem 1 with the application context, it is noted that the orness levelαshould be between 0.5 and 1.

2.3 Main advantages of ME-OWA operator method

The major advantages of the proposed method are presented as follows:

1) It is a well-developed method, which attracts much attention from the very beginning both in theory and application. It is simple, comprehensible, and convenient in application, and it has been used to aggregate information in certain areas.

2) The polynomial equation of the Liu method[21]of problem (9) is first used to determine the weighting vectors of the ME-OWA operator method, which is more simple.

3) It overcomes the fundamental shortcomings of the fuzzy RIM linguistic quantifier OWA operator method applied in aggregating metasearch engine results.

The fuzzy RIM linguistic quantifier OWA operator is more suitable for solving fuzzy aggregation problems. However, aggregating metasearch engine results is a crisp problem, and the weights obtained by the ME-OWA operator method are crisp numbers. The proposed method not only provides right multiple aggregation results for decision makers, but also has nearly the same aggregation results as those of the minimax-LP method.

4) It determines the optimal weighting vector under the maximal entropy, which has the ability to ascertain the optimal aggregation results after the aggregating processes.

When the orness levelα∈[0.5,1], the weights obtained by problem (9) monotonically decrease with the position index, which just satisfies the requirement of aggregating the retrieval document.α=1 is used to present the situation when the decision maker is maximally optimistic, andα=0.5 is used to represent the situation when the decision maker faces a moderate assessment.

3 Case Study of ME-OWA Operator Method

We now use the ME-OWA operator method to aggregate metasearch engine results, which is given by Amin and Emrouznejad[5]. The factors involve the number of search engines, the number of the first ranked list considered, the frequency of the document in every ranked place and the ME-OWA weighting vectors under different orness levels.

3.1 Computing process

Step1Four search engines SE1=Google, SE2=Yahoo, SE3=MSN and SE4=Altavista are selected. QueriesQ={metasearch engine, aggregation}are submitted to the four search engines.

Step2Suppose that we just rank the first ten documents retrieved from the four search engines, and there are 25 documents appearing in the first ten places, which is denoted asD1toD25.

Step3Count the frequency of each document appearing in each place within the four search engines, which is listed in Tab.2.

Tab.2 Frequency of the first ten results retrieved by four search engines

Step4Taken=10 andα=0.5 into Eq.(12), and obtainq=1.

Step5Takeq=1 into Eq.(11), and obtainw1=w2=…=w10=0.1.

Step6According to Eq.(1), the aggregation results of all the documents in Tab.2 are calculated, and we obtain

z1=0.4,z4=z9=z11=0.3

z2=z8=z12=z14=z15=z16=z17=0.2

z2=z5=z6=z7=z10=z13=z18=z19=…=z25=0.1

Step7By the same method, compute the weighting vectors and the corresponding aggregation results under the orness levelα=0.6,0.7,0.8,0.9,1.0, which are listed in Tab.3 and Tab.4, respectively.

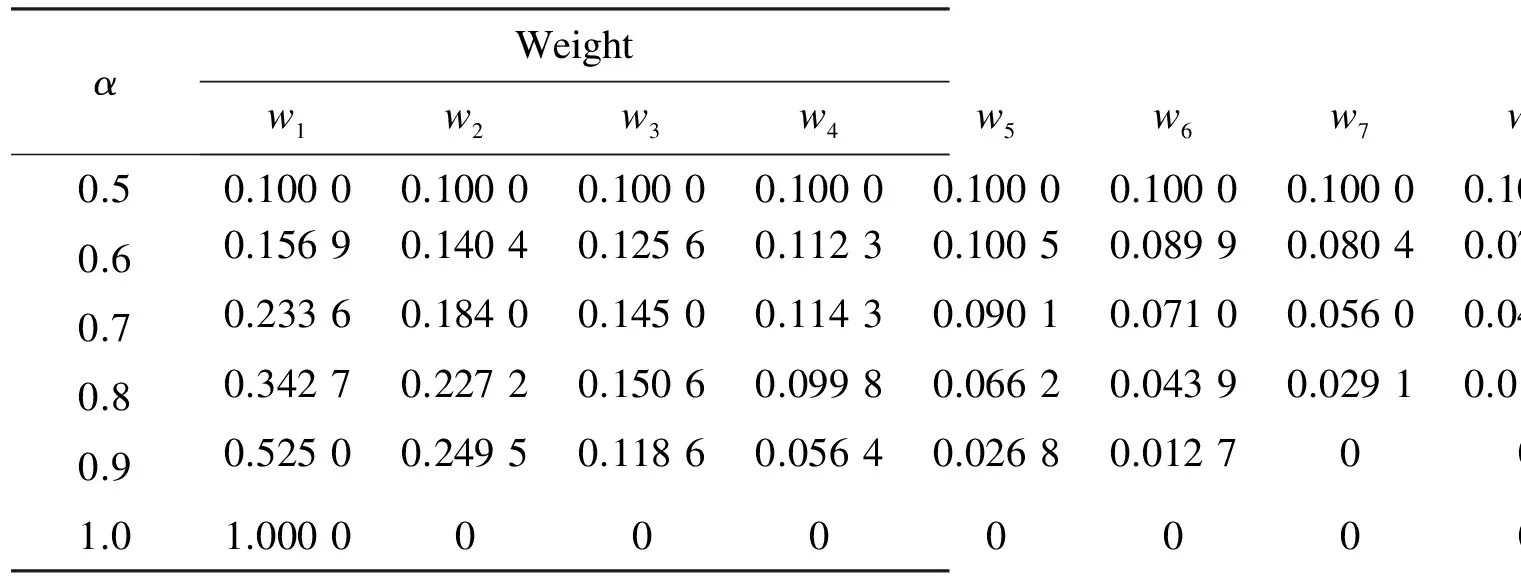
Tab.3 Weighting vectors in ME-OWA method

Tab.4 Aggregation results obtained by ME-OWA method

Step8Rank the first ten retrieval documents and compare them with those of the minimax-LP method, which is shown in Tab.5. The last column is calculated by the minimax-LP method[5].

Tab.5 Rank obtained by ME-OWA operator and minimax-LP method

3.2 Discussion

The characteristics of the proposed method are shown as follows:

1) It is noted that when the documents have the same aggregation results, the order in which the aggregation results are arranged is determined by the document position index. If there are more than ten qualified documents appearing in the final list, we just keep the first ten documents, and others will be omitted. For example, in Tab.4, whenα=0.5, documentsD3,D8,D12,D14,D15,D16andD17have the same aggregation result 0.2, and we order them according to their position index. In this case, documentD17is ordered in the 11-th place, so we omit it accordingly.

2) Compared with the minimax-LP method, from Tab.5, it is shown that some documents, e.g.,D1,D11,D9,D12, constantly have the same rank almost under all weighting vectors. Interestingly, whenα=0.6, the ranking is almost the same as that of the minimax-LP method.

Meanwhile, the proposed method fully considers people’s decision attitudes. Different orness levels will directly affect people’s decision results. However, the minimax-LP method cannot deal with them.

3) Compared with the existing methods based on the OWA operators[1,5], it not only deals with multiple crisp weighting vectors, but also has nearly the same aggregation results as those of the minimax-LP method.

4 Conclusion

We present a new decision making process based on the maximal entropy OWA operator and apply it in aggregating metasearch engine results problems. We study the main advantages of the new aggregation method and analyze the applicability of the proposed method. It is found that the proposed method is a more general formulation of the OWA operator. In this paper, we focus on an application under a metasearch engine context and see that depending on the aggregation operator, the results may lead to a different ranking, one of which is almost the same as that of the minimax-LP method.

[1]Diaz E D, De A, Raghavan V. A comprehensive OWA-based framework for result merging in metasearch[C]//LectureNotesinComputerScience. Springer, 2005,3542:193-201.

[2]Emrouznejad A. MP-OWA: the most preferred OWA operator[J].Knowledge-BasedSystems, 2008,21(8):847-851.

[3]Sugiura A, Etzioni O. Query routing for web search engines: architecture and experiments[J].ComputerNetworks, 2000,33(1/2/3/4/5/6):417-429.

[4]Keyhanipour A H, Moshiri B, Kazemian M, et al. Aggregation of web search engines based on users’ preferences in WebFusion[J].Knowledge-BasedSystems, 2007,20(4):321-328.

[5]Amin G R, Emrouznejad A. Finding relevant search engines results a minimax linear programming approach[J].JournalofOperationalResearchSociety, 2010,61(3):1144-1150.

[6]Amin G R, Emrouznejad A. Optimizing search engines results using linear programming[J].ExpertSystemswithApplications, 2011,38(9):11534-11537.

[7]Dreilinger D, Howe A E. Experiences with selecting search engines using metasearch[J].ACMTransInfSyst, 1997,15(3):195-222.

[8]Meng W Y, Yu C, Liu K L. Building efficient and effective metasearch engines[J].ACMComputSurv, 2002,34(1):48-89.

[9]Herrera-Viedma E, Gijón J L, Alonso S, et al. Applying aggregation operators for information access systems: an application in digital libraries[J].InternationalJournalofIntelligentSystems, 2008,23(12):1235-1250.

[10]De A, Diaz E D. Fuzzy analytical network models for metasearch[C]//StudiesinComputationalIntelligence. Springer, 2012,399:197-210.

[11]O’Hagan M. Aggregating template or rule antecedents in real-time expert systems with fuzzy set[C]//Proceedingsofthe22ndAsilomarConferenceonSignals,Systems,Computers. Piscataway, NJ: IEEE, 1988: 681-689.

[12]Fullér R, Majlender P. An analytic approach for obtaining maximal entropy OWA operator weights[J].FuzzySetsandSystems, 2001,124(1):53-57.

[13]Majlender P. OWA operators with maximal Rényi entropy[J].FuzzySetsandSystems, 2005,155(3):340-360.

[14]Xu Z S. An overview of methods for determining OWA weights[J].InternationalJournalofIntelligentSystems, 2005,20(8):843-865.

[15]Liu X W. Models to determine parameterized ordered weighted averaging operators using optimization criteria[J].InformationSciences, 2012,190(1):27-55.

[16]Yager R R. On ordered weighted averaging aggregation operators in multicriteria decision making[J].IEEETransactionsonSystems,ManandCybernetics, 1988,18(1):183-190.

[17]Zadeh L A. A computational approach to fuzzy quantifiers in natural languages[J].ComputingandMathematicswithApplications, 1983,9(1):149-184.

[18]Yager R R. Quantifier guided aggregation using OWA operators[J].InternationalJournalofIntelligentSystems, 1996,11(1):49-73.

[19]Liu X W, Han S L. Orness and parameterized RIM quantifier aggregation with OWA operators: a summary[J].InternationalJournalofApproximateReasoning, 2008,48(1):77-97.

[20]Filev D, Yager R R. Analytic properties of maximum entropy OWA operators[J].InformationSciences, 1995,85(1/2/3):11-27.

[21]Liu X W, Chen L H. On the properties of parametric geometric OWA operator[J].InternationalJournalofApproximateReasoning, 2004,35(2):163-178.