Research on development of urban taxi supply based on influence factors classification

Chen Jingxu Wang Wei Chen Xuewu Shen Jinshi

(School of Transportation,Southeast University,Nanjing 210096, China)

The taxi is gradually becoming a supplement to public transport due to its convenience, flexibility and door-to-door services. A number of studies have been conducted on different kinds of regulations with respect to the taxi market[1-4]and the development of taxi fleet size[5-7]. However, most of the current literature about the regulation of the taxi market comes from developed areas whose environments are quite different from those of mainland China. In China, entry regulation came into effect in the late 1990s. Despite limiting entry to the taxi industry, the government may artificially increase several hundred new taxis in one year as a result of the necessity of the urban development plans or for some occasional events (like holding an international sporting event). Such a particular year is described as a policy year for the taxi industry.

The development of taxi supply is also influenced by many non-policy factors, which can be divided into four parts, namely socioeconomic indices, scale and layout indices, other trip mode indices and tourism indices. But some newly-added number of taxis by the government as mentioned above cannot be explained by these factors. Thus, influence factors relevant to taxi supply involve two aspects: policy factor and non-policy factors (see Fig.1).

This paper concentrates on the analysis of the relationship between the taxi supply and influence factors. It utilizes an improved back-propagation neural network model. The model attempts to find out the policy years of the taxi industry and then investigate the relationship between the taxi supply and non-policy factors. A case study of Nanjing city is performed.

1 Modeling

A back-propagation (BP) neural network has advantages of self-learning, self-adapting and robustness. A three-layered BP neural network can be used to simulate nonlinear functions[8]. However, it has a poor speed of constringency, and it is easy to get stuck in a locally optimal solution. In order to overcome such disadvantages, a method combining the genetic algorithm (GA) with a BP neural network is used[9]. As a heuristic stochastic search algorithm, the GA does well in global searching, which can optimize the weights and thresholds in the BP neural network. Based on the improved BP neural network, this paper focuses on the identification of policy years and the relationship between the taxi supply and the influence factors. The process of the model is described below.

1.1 Normalization of data

Fifteen non-policy factors are scaled to the same range between 0 and 1 as

(1)

whereXijis the value of thej-th factor in thei-th year; max(Xj) is the maximum in the data set of the input sectorXj; and min(Xj) is the minimum in the data set of the input sectorXj.

The normalization of the taxi supply, which makes the value in a fixed interval [0,1], is given by

(2)

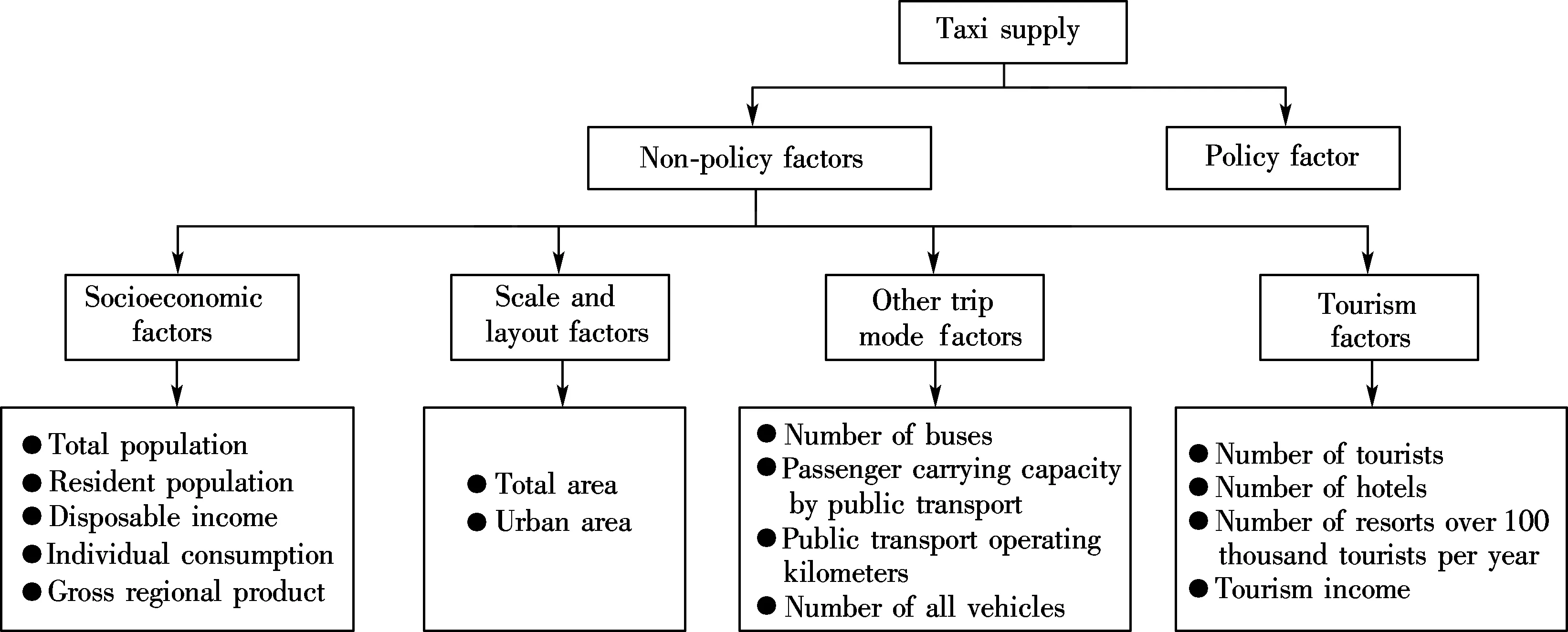
Fig.1 Influence factors relevant to the taxi supply

whereNiis the taxi supply of thei-th year;N0is the taxi supply of one year when the taxi market is in a free entry condition; andNmaxis the maximum taxi quantity based on the logistic model[10].

1.2 Model description

Fig.2 depicts the parallel distributed network which consists of three parts: an input layer, one hidden layer and an output layer.

In the input layer, fifteen non-policy factors after normalization procedures {μi1,μi2,…,μi15} are put into the input layer. The input layer has 15 nodes. In the hidden layer, thek-th hidden nodeνikis expressed as

(3)

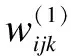
(4)

The optimization of weights and thresholds based on the GA is as follows:

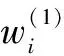
Step2Evaluate the fitness of all chromosomes by constructing the corresponding neural network. The objective function is described as

Fig.2 Basic architecture of the neural network used in this study

(5)

Step3Conduct the selection operation. We use the roulette wheel selection based on the ranking algorithm. After conducting the selection operator, the intermediate population is created by extracting chromosomes from the current population. The selection probability for the individualmis

(6)

whereMis the number of chromosomes andfmis the fitness of individualm.

Step4Execute the crossover operation. According to the crossover probabilitypc(Assume thatpc=0.7), the parent individuals produce a new generation through linear crossovers. The chromosomesamandalconducting the crossover process athis expressed as

(7)

wherebis the random number located in the interval (0,1).

Step5Implement the mutation operation. The mutation parent individuals are randomly chosen based on the mutation probabilitypm(Assume thatpm=0.01). The variation process for the geneamhis given as

(8)

whereamaxis the upper limit ofamh;aminis the lower limit ofamh;ris the random number located in the interval (0,1);f(g)=r(1-g/Gmax);gis the current number of iterations; andGmaxis the maximum number of generations.

Step6Examine whether the fitness degree exceeds the given precision requirement (It is set to be 108) or the number of generations attains the presumed maximum value. If it does not satisfy, repeat step 2 to step 5 until the terminal condition is met.

The learning process of the optimum BP neural network is as follows:

Step1The BP neural network weights and threshold values are initialized as the chromosome of the best fitness population member based on the GA.

Step2Calculate the values of the hidden layer and the output layer as presented in Eqs.(3) and (4).

Step3The mean square error function is adopted as the error function, which is defined as

(9)

Step4The error in the output layer is propagated backward to hidden layer neurons, and then to input layer neurons revising the weights and threshold values by the Levenberg-Marquardt method.

Step5Repeat step 2 to step 4 until the error is reduced to a predetermined convergence tolerance or the iteration number attains the maximum iteration number (Assume that the target error is 10-6and the maximum iteration number is 104).

2 Case Study

Nanjing is selected as the study area, and the data source in this paper comes from the statistical yearbook of Nanjing[11].

2.1 Identification of policy years of taxi industry

Nanjing began to implement entry regulations in 1997, and in the later three years there were no big events or exigent requirements for an expansion of the taxi market. Thus, it is assumed that there is no policy year of the taxi industry from 1997 to 1999. The identification procedure is as follows:

Step1Data from the yeart-3,t-2,t-1 is put into the improved neural network model for training, and the data from the yeartis used for identifying whether the yeartis a policy year (The year 2000 is the first testing year). If the relative error between the desired output and the actual output exceeds 5%, the yeartis identified as a policy year of the taxi industry and go to step 2; if not, go directly to step 3.

Step2The difference value between the desired output and the actual output can be seen as the newly-added taxi quantity in one policy year. As the local government may artificially put several hundred taxis one-off or in batches[3-4], the newly-added number is rectified as

(10)

Step3Examine the yeart. If the yeartis the last testing year, 2011, the process of identification is over; if not, lett=t+1 and return to step 1.

Tab.1 shows the results of the identification of the policy years. The years 2001 and 2007 are the policy years of the taxi industry. Referring to the five-year plan of China and the local government reports about the taxi industry, it is noteworthy that the results of identification are basically in accordance with these development plans.

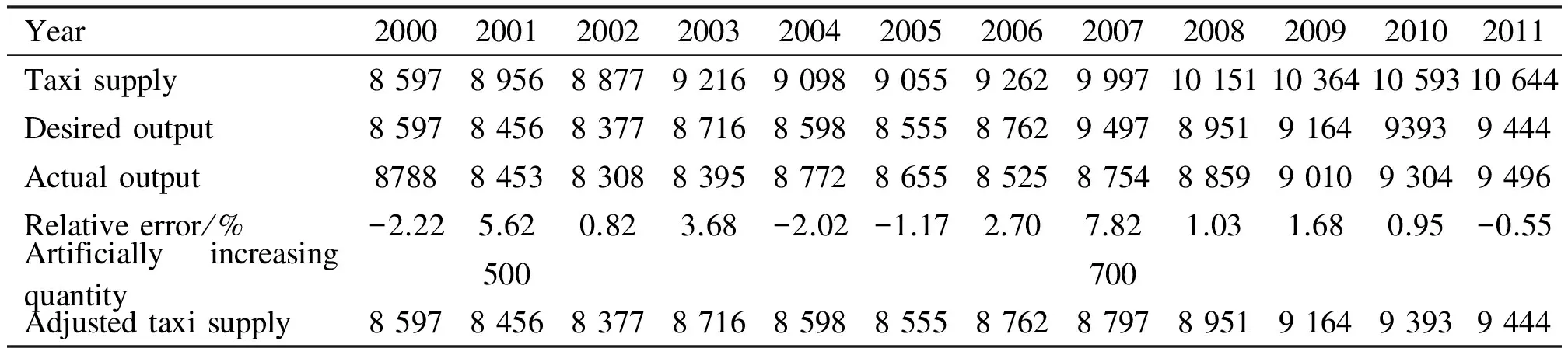
Tab.1 Indentification of the policy years of taxi industry in Nanjing

At the beginning of 2001, according to the 10th five-year plan (2001—2005), the local government of Nanjing decided to prioritize the tourism industry and encourage Nanjing to be an international tourism city. When tourists (especially foreigners) are in an unfamiliar tourist city, they may choose taxis as their main trip mode. Besides, the statistical yearbook of Nanjing indicates that the number of tourists ascended visibly during the 10th five-year plan. Therefore, it is reasonable that the local government put 500 new taxis into the taxi market in 2001, and 2001 should be a policy year. When it comes to the 11th five-year plan (2006—2010), the major plan of local government was primarily to develop two rural areas (Jiangning District and Pukou District), which are expected to become centers of technological research and innovative startups. But these two districts lag behind in transport infrastructure, and it may be a reason for the government to add 700 new taxis in 2007, and 2007 can be regarded as a policy year. The adjusted values of the taxi quantity, excluding the political influence, are presented in the last column of Tab.1.

2.2 Interactionbetweentaxisupplyandnon-policy factors

After subtracting the political influence, it is more accurate to get the interplay between the development of the adjusted taxi supply and the non-policy factors based on the established model once again.

The normalized data from 1997 to 2008 constitute the training set and the remaining normalized data (from 2009 to 2011) are used in the testing phase. The input vector is represented by fifteen normalized non-policy factors. Accordingly, the output vector represents the normalized values for the adjusted taxi quantity. The training parameters are as follows: The population sizeNis 50; the number of evolution generation is 200; the crossover probabilitypcis 0.7; the mutation probabilitypmis 0.01; and the training precision is 10-6. The outputs and relative errors of the testing data are shown in Tab.2.

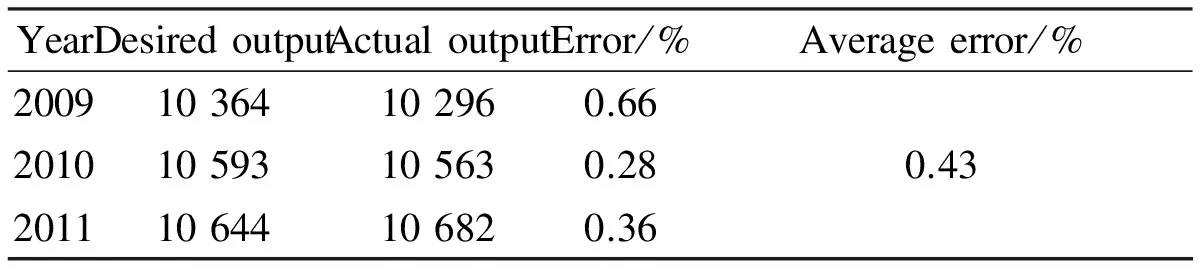
Tab.2 Simulation results and errors of testing data

In Tab.2, based on the trained neural network model, the actual output simulated with the testing input data shows good agreement with the adjusted taxi quantity. Compared with the original BP neural network and the ARMA time series forecasting method[12](The average errors are 1.46% and 2.99%, respectively.), the model developed in this paper has a better performance in finding the relationship between adjusted taxi quantity and non-policy factors.

Besides, the model can be utilized to calculate the predicted values of 15 non-policy factors from 2012 to 2015, and then forecast the taxi supply of Nanjing. The predicted values of the taxi supply in the next four years (2012—2015) are 10 763, 10 842, 10 895 and 10 847, respectively. Overall, future taxi supply will continually experience a slow increase trend, while fluctuating within a narrow range. It is just in accordance with the characteristics of the taxi market in Nanjing under strict entry regulation.

3 Conclusions and Future Work

Since the late 1990s, the majority of Chinese cities have regulated their taxi markets. Meanwhile, the local government still artificially adds some new taxis for the necessity of the urban development plans. In this paper, an improved neural network model is utilized, and a case study of Nanjing city is performed. First, the model is applied to identify the policy years of the taxi industry and then adjust the taxi quantity to exclude the political influence. The identified results are in accordance with the five-year plan of China and the local government reports about the taxi market. Thus, 2001 and 2007 can be seen as policy years of the Nanjing taxi market. Then the interactions between the adjusted taxi supply and non-policy factors are studied based on the model once again. The simulation results exhibit that the model has a good performance in finding the relationship between the adjusted taxi supply and non-policy factors. In the future, we will establish a demand model of the taxi market and explore the demand-supply relationship in the taxi industry, and try to predict potential policy years of the taxi industry.

[1]Flores-Guri D. An economic analysis of regulated taxicab markets [J].ReviewofIndustrialOrganization, 2003,23(3):255-266.

[2]Schaller B. Entry controls in taxi regulation: implications of US and Canadian experience for taxi regulation and deregulation [J].TransportPolicy, 2007,14(6): 490-506.

[3]Yao Zhigang, Cheng Gao. Clustering taxi quantity regulatory levels of Chinese capital cities[J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2012,12(5):1-6.

[4]Tian W J. Investigating the regulations of the taxicab market in Chinese large cities [D]. Wuhan: Zhongnan University of Economics and Law, 2010. (in Chinese)

[5]Xu J M, Wong S C, Yang H, et al. Modeling level of urban taxi services using neural network [J].JournalofTransportationEngineering, 1999,125(3): 216-223.

[6]Yang H, Lau Y W, Wong S C, et al. A macroscopic taxi model for passenger demand, taxi utilization and level of services [J].Transportation, 2000,27(3): 317-340.

[7]Salanova J M, Estrada M, Aifadopoulou G, et al. A review of the modeling of taxi services [J].Procedia—SocialandBehavioralSciences, 2011,20: 150-161.

[8]Whitley D, Starkweather T, Bogart C. Genetic algorithms and neural networks: optimizing connections and connectivity [J].ParallelComputing, 1990,14(3): 347-361.

[9]Wen X L, Song A G, Duan J H, et al. Evolving neural networks using an improved genetic algorithm [J].JournalofSoutheastUniversity:EnglishEdition, 2002,18(4):367-369.

[10]Miranda L C, Lima C A. On the logistic modeling and forecasting of evolutionary processes: application to human population dynamics [J].TechnologicalForecastingandSocialChange, 2010,77(5): 699-711.

[11]National Bureau of Statistics of China.ThestatisticalyearbookofNanjing[M]. Beijing: China Statistics Press, 1995—2012.

[12]Box G E P, Jenkins G M.Timeseriesanalysis:forecastingandcontrol[M]. San Francisco, CA, USA: Holden Day, 1978.