Effective thermal and electrical conductivity of graphite nanoplatelet composites

Zhou Xiaofeng Zhang Xiaosong Zhou Jiancheng

(1School of Energy and Environment, Southeast University, Nanjing 210096, China)(2Department of Fundamental Sciences, Yancheng Institute of Technology, Yancheng 224003, China)(3School of Chemistry and Chemical Engineering, Southeast University, Nanjing 211189, China)

Recently, there has been an increasing interest in graphite nanoplatelet composites because of their unique electrical, thermal and optical properties[1-6]. The thermal conductivity of large enough graphite nanoplatelets (GNPs) should be higher than that of bulk graphite[7]. Recent experimental studies have also shown that the thermal conductivity of few-layer GNPs is of a similar aspect ratio to that of single-wall nanotubes (SWNTs) but with twice the increase in the thermal conductivity when embedded in epoxy composites[8]. Moreover, the nonlinear dependence of the effective thermal conductivity on the volume fraction of GNPs has been reported[7]. In the case of the electrical conductivity, very low percolation thresholds in carbon nanotube composites have also been reported[9-10]. Surprisingly, the thermal transport measurements on GNP-oil nanofluids bear no signature of the percolation threshold. The contrasting behavior should be carefully examined since both the thermal and electrical transport processes are described by the same continuum equation[11-12]. The relationship between the thermal/electrical conductivity enhancement and the properties of filling GNP particles requires quantitative study of the thermal/electrical transfer processes in GNP composites.

1 Experiment

In this paper, we study the thermal conductivity enhancement of GNP-oil nanofluids and the low percolation threshold of GNP-polyimide composites. Considering the shape and the volume fraction of graphite nanoplatelet particles, we would like to generalize the effective medium theory to investigate the effective thermal and electrical properties of GNP composites. Our theoretical prediction on the effective thermal and electric conductivity of GNP composites is in good agreement with the experimental results.

Graphite nanoplatelet particles are grown on substrates by the ultrasonic spry pyrolysis method and under the typical controlled exfoliation and dispersion process[8, 13]. In order to investigate the effective thermal conductivity enhancement of GNP-oil nanofluids, the GNP particles of 0.05%, 0.1%, 0.2%, 0.4%, 0.6%, 1.0% in volume fraction are chosen. Then the chosen amount of GNP particles are filled into the base oil liquid and operated under a high rotation speed for about 100 min to ensure a good dispersion of additional filling GNP particles in oil. The thermal conductivity of GNP-oil nanofluids is measured by a thermal testing device (ZKY-BRDR). The effective electric conductivity enhancement of GNP-polyimide composites is measured by a resistivity test fixture (Keithley8009) and an electrometer (Keithley6517).

2 Results and Discussion

To observe details of the as-prepared graphite nanoplatelet particles, a scanning electron microscope (SEM) and high resolution transmission electron microscopy (TEM) are employed. The results are shown in Fig.1. From Figs.1(a) and (b), it can be seen that the average lateral dimensions and the average thicknesses of GNPs are 0.5 to 3 μm and 10 to 20 nm, respectively. The SEM and TEM images show that the as-prepared products consist of nanoplatelets with irregular shape and thickness distribution.

In the course of understanding the transport behavior of the GNP mixture, we would like to generalize the effective medium theory[14]. We consider a graphite nanoplatelet composite in which the graphite nanoplatelet particles with the volume fractionfand matrix particles with conductivityKmare randomly mixed. For simplicity, we assume that matrix particles are spherical and graphite nanoplatelet particles are spheroidal in shape with the half radiia,b,c, andb=c. Since graphite nanoplatelet particles are randomly oriented, the effective conductivityKeis isotropic[15-16]. For such a composite, the effective medium theory gives[17]that

(1)

whereKc,jis the equivalent thermal (or electrical) conductivity along thej-axis, and the depolarization factorLjdepends on the GNP aspect ratioP=a/c, which is expressed as

(2)

For the thermal transportation, due to the large interfacial thermal resistance, graphite nanoplatelet particles are physically anisotropic. In order to take such an effect into account, one often assumes that spheroidal particles are coated with a layer of material with thicknessdand conductivityKs. The interfacial thermal resistance is concentrated on a surface of zero thickness, which is defined as

Hence, one hasKc,j=Kp/(1+QRBdLjKp)withQ=(2a+c)/(ac). As a result, Eq.(1) is simplified as

(3)

For the electrical transport, the interfacial electrical resistance is so small that it can be ignored, i.e.,RBd=0. Therefore, we calculate the effective electrical conductivity by substitutingKc,j=Kpinto Eq.(3). Note that Eq.(3) can predict the non-zero percolation threshold.

Fig.2 shows a comparison between Eq.(3) and our measured effective thermal conductivity of GNP-oil nanofluids. In the calculation, the thermal conductivities of the oil and the GNPs are taken as 0.1448 and 1000 W/mK, respectively[8], andRBd=8×10-8m2·K/W. In addition, the depolarization factor tends to be zero for graphite nanoplatelet particles with a large aspect ratio. Fig.2 shows the thermal conductivity enhancement as a function of the filler loading. The enhancement (as high as 50%) in the thermal conductivity is observed for the GNP-oil nanofluids with a volume fraction of only 1% GNPs. At the same time, our theoretical results are found to be in reasonably good agreement with the measured experimental data.

Fig.2 Effective thermal conductivity enhancement of GNP-oil nanofluids compared with the theoretical results

Fig.3 shows the enhancement of the effective electrical conductivity vs. the volume fraction in GNP-polyimide composites. We can see that the theoretical results are in good agreement with the measured experimental data. For GNPs in polyimide composites, the depolarization factor is estimated as 0.00007; hence,fc=0.0004. Such a percolation value is of the same order as the data reported in Ref.[11]. When the experimental data is compared with our theoretical results, we find that a very low percolation threshold for GNP-polyimide composites is well predicted.

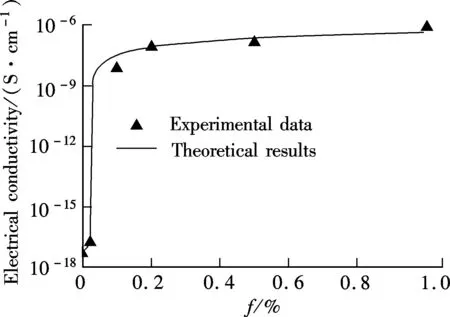
Fig.3 Effective electrical conductivity vs. volume fraction in GNP-polyimide composites

3 Conclusion

The effective thermal and electrical conductivity enhancements of GNP-oil nanofluids and GNP-polyimide composites are measured. As high as 50% enhancement in the thermal conductivity is observed for GNP-oil nanofluids with a volume fraction of only 1%. For the GNP-polyimide composites, the non-zero percolation threshold is well investigated. Both the nonlinear dependence of the effective thermal conductivity on the GNP volume fraction in nanofluids and the very low percolation threshold for GNP-polyimide composites are well predicted. Our theoretical predications are in good agreement with the experimental data. Our model can be applied for predicting the thermal and electrical properties of GNP composites, which is still available for most of the thermal/electrical modification in two-phase composites.

[1]Novoselov K S. Electric field effect in atomically thin carbon films [J].Science, 2004,306(5696): 666-669.

[2]Novoselov K S. Two-dimensional gas of massless Dirac fermions in grapheme [J].Nature, 2005,438(9):197-200.

[3]Zhang Y B,Tan Y W, Stormer H L, et al. Experimental observation of the quantum Hall effect and Berry’s phase in grapheme [J].Nature, 2005,438(9): 201-204.

[4]Nair R R. Fine structure constant defines visual transparency of grapheme [J].Science, 2008,320(5881):1308-1310.

[5]Balandin A A. Superior thermal conductivity of single-layer grapheme [J].NanoLetter, 2008,8(3): 902-907.

[6]Ghosh S. Extremely high thermal conductivity of graphene: prospects for thermal management applications in nanoelectronic circuits [J].AppliedPhysicsLetter, 2008,92(15):151911-151913.

[7]Yu A, Itkis M E, Bekyarova E, et al. Effect of single-walled carbon nanotube purity on the thermal conductivity of carbon nanotube-based composites [J].AppliedPhysicsLetter, 2006,89(13):133102-133103.

[8]Aiping Y, Palanisamy R, Mikhail E I, et al. Graphite nanoplatelet-epoxy composite thermal interface materials [J].JournalofPhysicsChemistryLetterC, 2007,111(75): 7565-7569.

[9]Bryning M B, Islam M F, Kikkawa J M, et al. Conductivity threshold in bulk isotropic single-walled carbon nanotube—epoxy composites [J].AdvancedMaterials, 2005,17(11): 1186-1191.

[10]Ounaies Z, Park C, Wise K E, et al. Carbon nanotube polymer composites [J].CompositesScienceTechnology, 2003,63(16): 1637-1646.

[11]Shenogina N, Shenogin S, Xue L, et al. On the lack of thermal percolation in carbon nanotube composites [J].AppliedPhysicsLetter, 2005,87(13): 133106-133108.

[12]Foygel M, Morris R D, Anez D, et al. Theoretical and computational studies of carbon nanotube composites and suspensions: electrical and thermal conductivity [J].PhysicalReviewB, 2005,71(10): 104201-104208.

[13]Wang S Y, Wang W, Wang W Z, et al. Preparation and characterization of highly oriented NiO(200) films by a pulse ultrasonic spray pyrolysis method [J].ScienceEngineeringB, 2002,90(10): 133-137.

[14]Sheinman M, Broedersz C P, MacKintosh F C, Nonlinear effective-medium theory of disordered spring networks [J].PhysicalReviewE, 2012,85(2):021801-021816.

[15]Nan C W, Liu G, Lin Y H, et al. Interface effect on thermal conductivity of carbon nanotube composites [J].AppliedPhysicsLetter, 2004,85(35): 3549-3551.

[16]Lin C G, Chung D D L. Graphite nanoplatelet pastes vs. carbon black pastes as thermal interface materials [J].Carbon, 2009,47(6): 295-305.

[17]Zhou X F, Wang S Y. Thermal conductivity and insulation modification in asphalt-based composites [J].JournalofMaterialsScienceandTechnology, 2012,28(3): 285-288.