月球探测器定轨误差分量协方差分析

樊敏 董光亮 郝万宏 王宏

（北京跟踪与通信技术研究所，北京 100094）

1 引言

在月球探测任务分析与设计阶段，通常需要对地月转移、月球捕获、环月飞行等各轨道段的定轨预报精度进行全面分析，以确定中途修正、近月制动和动力下降等关键点的轨道精度，这是测控系统总体设计需要约定的重要指标之一。常用的环月轨道精度表示方式是定轨预报误差及其RTN 方向的分量，其中R 方向指从月心指向探测器的方向，N 方向指轨道面法向，T 方向指在轨道面内与R、N 方向构成右手系的方向。考虑到定轨预报过程的复杂性，定轨误差分量受到测量条件、轨道特性、地月位置关系等因素的影响，而且这些因素的作用是非线性的，因此，给出环月轨道定轨误差RTN 分量的合理指标是一个难题。

针对上述问题，本文对测距、测速和干涉测量手段获取的测量量建立测量模型，确定探测器状态矢量的信息阵和误差协方差矩阵，进而推导出定轨误差RTN 分量的误差方程和协方差矩阵，给出测量误差对定轨误差RTN 分量影响的数值关系。考虑到中国探月工程二期任务将实施月球软着陆和巡视探测，开展月表地形地貌、月球地质构造、地月空间与月表环境探测和月基光学天文观测等活动［1］，为了保证着陆器能成功着陆到指定的着陆区，在任务分析与设计阶段就要重点分析动力下降初始轨道定轨误差及其RTN 方向的分量。为此，本文在理论分析的基础上，根据中国探月工程二期任务的测站／基线分布情况，分析了不同环月轨道探测器位置误差和速度误差RTN分量的影响因素、误差水平及3个方向的误差分量，给出了不同环月轨道的位置误差和速度误差的各方向分量的不同特征。

2 测量模型和信息阵

中国月球探测任务的测定轨系统为S频段统一测控系统＋甚长基线干涉测量（USB＋VLBI）综合系统，它充分利用了USB 系统高精度测距测速和VLBI系统高精度测角的能力。在动力下降前的环月100km／15km 轨道段，测距测速数据由喀什站和佳木斯站获取，VLBI干涉测量数据由上海站、乌鲁木齐站、北京站和昆明站组成的不同基线获取。在深空站和VLBI三站共视弧段内，测量数据包括1个测站获取的测距ρ、测速ρ和2条不同基线获取的时延D1、D2以及时延率D1、D2。

为了便于分析，在J2000地心天球坐标系中建立测距、测速和干涉测量时延、时延率测量量与探测器状态矢量之间的关系，如图1 所示［2］。其中：αg为格林尼治子午线的赤经；探测器状态矢量的球坐标形式Xsph的分量为（r，α，δ，r，α，δ），直角坐标形式Xcar的分量为（x，y，z，x，y，z）；测站坐标为（rs，zs，φ），测站位置矢量的柱坐标形式Rsta的分量为（rscosφ，rssinφ，zs）。

图1 J2000地心天球坐标系中的探测器状态矢量和测站位置矢量Fig．1 Probe state vector and station position vector in J2000geocentric celestial system

2．1 测距和测速的测量模型和信息阵

在图1所示的坐标系中，测站的测距模型表示为式（1）。对于环月探测器，rs／r≪1和zs／r≪1成立。

式中：ρ为测站到探测器的距离。

将式（1）右端关于rs／r和zs／r展开［3］，可得

略去式（2）中rs／r和zs／r的高阶项，并且将探测器位置矢量由直角坐标形式替换为球坐标形式，可得

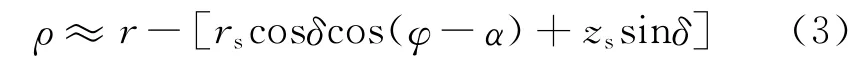
测距观测量包含的轨道信息内容可由信息阵定义，测距数据的信息阵为

式中：为测距数据误差的方差。对式（3）两端关于时间t求导，可得测速模型的近似表达式为［3］

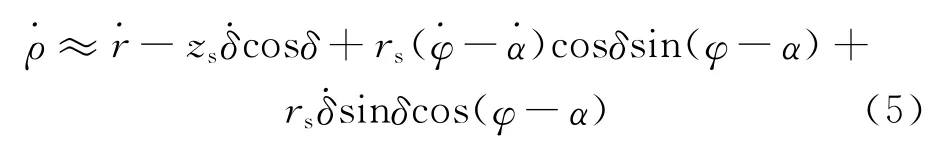
式中：≈ωe，其中ωe为地球自转平均角速度。

测速数据的信息阵为

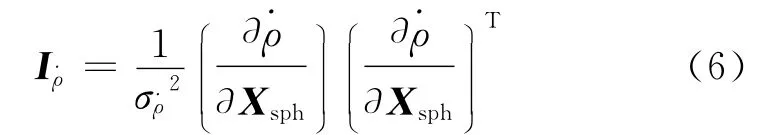
式中：为测速数据误差的方差。

2．2 时延和时延率的测量模型和信息阵

传统的测距、测速数据能够给出探测器在测站视向上的参数，对垂直于视向的横向参数不敏感［4］。对于探月及更远的深空探测任务，在某些特定的测站几何构形条件下，只利用测距、测速数据，缺乏横向角度信息的约束，会将探测器测站视向距离上的扰动估计为横向（或天平面）位置上的偏差［5］。VLBI能够对天体实现高精度的测角，而且具有测量周期短、测角精度高、只需发送下行信号等优势［6］。经过数十年的发展，VLBI技术在各国深空探测器导航和相关科学领域得到了广泛应用。美国国家航空航天局（NASA）的“火星勘测轨道器”（MRO）任务实现了2nrad的测角精度，日本宇宙航空研究开发机构（JAXA）的“月亮女神”（SELENE）任务对2个子探测器进行同波束干涉测量（SBI），时延精度达到皮秒级［7］。因此，中国探月工程采用测距测速＋VLBI干涉测量联合测轨体制进行轨道确定［8］。下面分析干涉测量时延、时延率数据的测量模型。

由于环月探测器距离地球很远，时延测量量Ddelay可由式（7）近似计算。

式中：B为基线矢量，其柱坐标形式rB的分量为（rBcosφB，rBsinφB，zB），测站1、2的位置矢量柱坐标形式r1和r2的分量分别为（r1cosφ1，r1sinφ1，z1）和（r2cosφ2，r2sinφ2，z2），其中，rB＝［（r1cosφ1-r2cosφ2）2＋zB＝z1-z2，φB ＝arctan［（r1sinφ1-r2sinφ2）／（r1cosφ1-r2cosφ2）］；s为探测器-地心单位方向矢量，分量为（cosδcosα，cosδsinα，sinδ）。

根据时延的近似计算公式有［9］

式中：基线时角HB＝φB-α。

时延观测量的信息阵为

对式（8）两端关于时间t求导，可得时延率的近似表达式为［10］

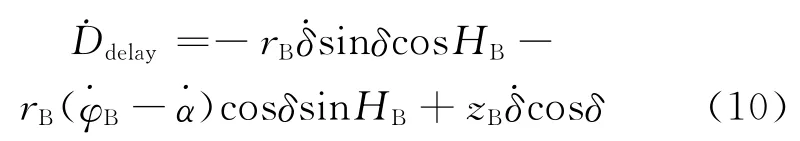
时延率观测量的信息阵为

田卓听完汇报也很兴奋，鼓励大家再努力一把，争取在两个月之内，就给这个活动画上一个完美的句号。临散会的时候，田卓还专门安排高潮说，高先生，你该提前做新的项目策划了。从田卓的话音里，高潮可以感觉出她对自己的策划能力认可了，心里的兴奋又陡增了几分。

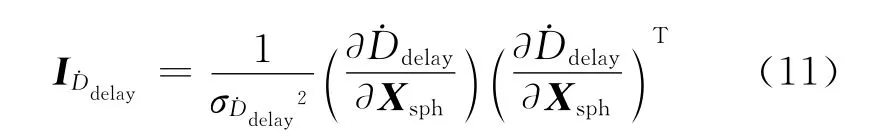
3 误差方程和误差协方差矩阵

根据第2节给出的各种测量数据的测量模型，可以建立测量量Y和探测器状态矢量Xsph之间的误差方程。

探测器状态矢量的误差协方差矩阵为

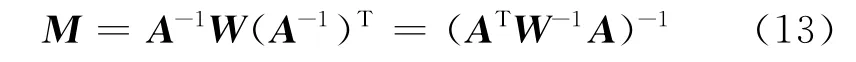
式中：W为以测量量的误差方差为对角线元素的对角矩阵。

根据测量量的信息阵，可得测量量信息阵和的逆矩阵为误差协方差矩阵，见式（14）。

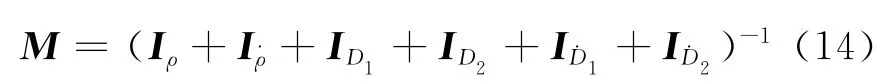
式中：Iρ、Iρ、ID1、ID2、ID1和ID2分别为1个测站的测距ρ、测速ρ和2条不同基线获取的时延D1、D2以及时延率D1、D2的信息阵。

将式（15）记为XMJ2000＝F（Xsph），其中F表示式（15）所确定的函数关系。对此式两端进行全微分，在小偏差条件下，以增量符号代替微分符号，可得

根据式（12）可以建立探测器相对月心的状态矢量和测量量之间的误差方程，见式（17）。

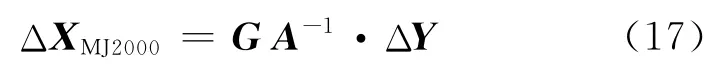
探测器相对月心状态矢量的误差协方差矩阵为

根据RTN 方向的定义设定：R 方向的单位矢量为SR＝rMJ2000／｜rMJ2000｜，N 方向的单位矢量为SN＝rMJ2000×rMJ2000／｜rMJ2000×rMJ2000｜，T 方向的单位矢量为ST＝SN×SR。其中，rMJ2000和rMJ2000分别为探测器在J2000 月心天球坐标系（MJ2000）中的位置 和 速 度 矢 量，其 分 量 分 别 为 （xMJ2000，yMJ2000，zMJ2000）和（xMJ2000，yMJ2000，zMJ2000）。将探测器相对月心状态矢量的误差投影到轨道的RTN 方向，可以得到位置误差ΔP和速度误差ΔV的RTN 分量，综合考虑式（18），可得

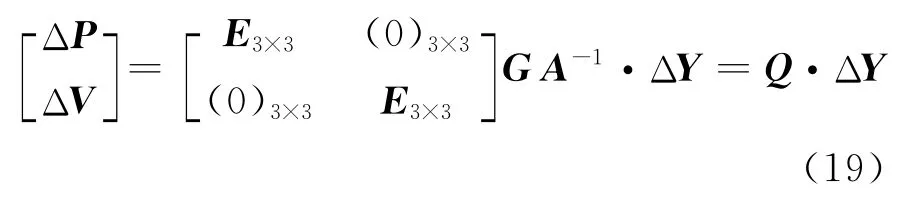
式中：E3×3是由单位矢量SR、ST和SN构成的3×3矩阵；Q为探测器相对月心的状态矢量误差方程的系数矩阵。

探测器相对月心状态矢量的RTN 分量的误差协方差矩阵为

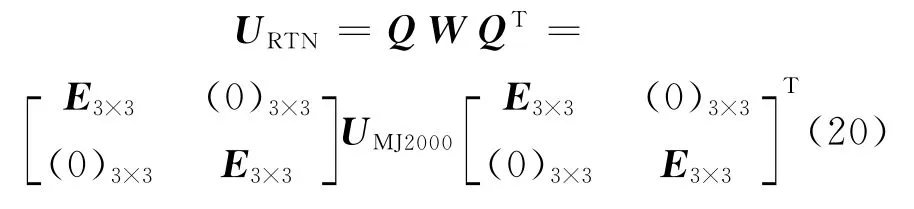
由于误差方程的系数矩阵Q和误差协方差矩阵URTN的表达式涉及到探测器的状态矢量、各测站／基线的位置矢量及变化率等多个变量及其相互关系式，表达式非常复杂，略去推导的过程，直接给出分析结果如下。

1）位置误差的RTN 分量（ΔPR、ΔPT和ΔPN）

ΔPR、ΔPT和ΔPN均与Δρ、ΔD1和ΔD2相关，即探测器位置误差受到测距、2条基线的时延测量误差的影响。根据上述计算结果可得

式中：下标C分别代表R、T 和N，相应的SC分别代表单位矢量SR、ST和SN；αi，βi，γi（i＝1，2）为基线对位置误差的影响系数。

由式（21）可见，位置误差的RTN 分量主要与探测器相对月心的位置矢量对（r，δ，α）偏导数的RTN 分量相关，还与测站／基线的时角、测站地心距及基线长度等因素相关。

2）速度误差的RTN 分量（ΔVR、ΔVT和ΔVN）

ΔVR、ΔVT和ΔVN均 与Δρ、Δρ、ΔD1、ΔD1和ΔD2、ΔD2相关，即探测器速度误差受到测距、测速、2条基线的时延、时延率测量误差的影响。根据上述计算结果可得

式中：α′i，β′i，γ′i，ε′i，η′i，ξ′i（i＝1，2，3，4）为基线对速度误差的影响系数。

由式（22）可见，速度误差的RTN 分量与探测器相对月心的状态矢量对（r，δ，α，r，δ，α）偏导数矢量的RTN 分量相关，也与测站／基线的时角、测站地心距及基线长度等因素相关。

4 不同环月轨道的误差RTN 分量

根据上述分析可知，当测站／基线位置、测量类型和测量精度已经确定时，探测器定轨误差的RTN 分量主要与其状态矢量、测站／基线的时角及变化率有关，即主要与轨道特性和测站／基线与探测器之间的几何关系有关。下面在给定测站／基线位置、测量类型和测量精度的情况下，分析2 种典型环月轨道的误差RTN 分量的影响系数和误差水平。

选取中国4个VLBI测站中的2条基线——基线1（佘山-乌鲁木齐）、基线2（密云-昆明）和USB测站中的青岛站，参考历元时刻为2010-10-28 T16：10：00．00（UTC），测 量 精 度 为σρ＝5 m，σρ＝1cm／s，σD＝5ns，σD＝1ps／s。2 种不同类型环月轨道的轨道根数如表1所示。

表1 2种轨道具体轨道根数（月心J2000惯性坐标系）Table 1 Elements of two orbits（J2000lunarcentric inertia system）

根据上述误差协方差分析过程，可以计算出2种不同轨道的位置误差和速度误差RTN分量的均方差和部分影响系数，如图2和表2所示。由此可见，对于2种不同的轨道，当测站／基线位置、测量类型和测量精度已经确定时，位置误差和速度误差的量级一致，但误差RTN 分量有明显差别。误差RTN 分量的具体特征如下。

（1）对于轨道1，位置误差和速度误差的RTN分量特征类似，即R 方向和T 方向分量相当，约为N 方向分量的1／2。

（2）对于轨道2，位置误差和速度误差的RTN分量特征不同。位置误差的R 方向和T 方向分量相当，约为N 方向分量的9倍；速度误差的T 方向分量最大，约为N 方向分量的6 倍，R 方向分量次之，约为N 方向分量的5倍。

（3）比较各测量量对RTN 分量的影响可得：对于轨道1，测距量对N 方向分量影响相对较小，基线1时延量对R、T、N 方向影响较平均，基线2时延量对N 方向影响较大；对于轨道2，测距量对N方向分量影响相对较大，基线1 时延量对T 方向影响较大，基线2时延量对R 方向影响较大。

根据上述分析过程，对嫦娥-1、2（Chang’e-1、2）月球探测器的100km／15km 环月轨道近月点位置速度误差的RTN 分量进行分析，将误差RTN分量的均方差与实测数据定轨结果进行比较，如表3 所示。可以看出，由于分析中仅考虑测量误差，而实际定轨误差还受到模型误差、测量数据精度等多种因素的制约，因此2 种结果的误差RTN 分量具体值有所差异，但是各误差分量的大小比例和特征类似。在后续任务总体设计过程中，可以参考已有任务环月轨道的位置和速度总误差，利用本分析方法对误差RTN 分量进行分配，得到定轨误差的RTN 分量作为参考值。

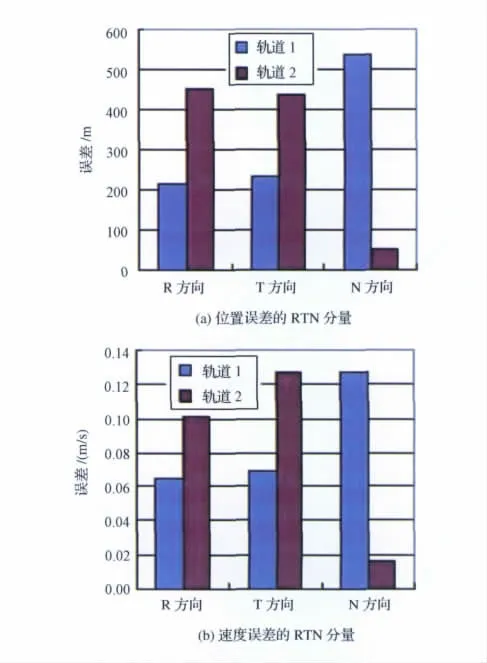
图2 不同轨道的位置误差和速度误差的RTN 分量Fig．2 RTN components of errors in position and velocity for various orbits

表2 各种测量量对不同轨道的位置误差RTN 分量的影响系数Table 2 Influence coefficients of each measurement for RTN components of position errors of various orbits

表3 嫦娥-1、2定轨误差RTN 分量的均方差Table 3 RMS of RTN components of orbit-determination errors for Chang’e-1and Chang’e-2probes

5 结束语

本文首先根据各种测量数据的定义和近似公式，建立了中国探月工程中使用的轨道测量数据关于月球探测器状态矢量的模型，确定了状态矢量的信息阵和误差协方差矩阵；然后，推导了环月轨道定轨误差RTN 分量的误差方程和协方差矩阵，给出了测量误差对定轨误差RTN 分量影响的数值关系，在此基础上，考虑中国探月工程中测控系统测站／基线分布情况和测量精度，分析了2种不同环月轨道位置误差和速度误差RTN 分量的影响因素、误差水平及3个方向的误差分量；最后，利用嫦娥-1、2探测器100km／15km 环月轨道实际定轨结果，验证了分析方法的有效性。这种分析方法对于中国探月工程二期任务动力下降初始轨道位置误差和速度误差RTN 分量计算具有参考意义。随着中国未来月球与深空任务论证分析工作的逐步开展，探测器系统对关键轨道机动时刻定轨误差RTN 分量的需求将会更加明确，后续应考虑多种误差因素以及不同测量弧段和测量数据类型对定轨误差RTN 分量的影响，进而补充、完善该分析方法，这将有利于测控系统对误差RTN 分量进行准确、细化分析。

（References）

［1］褚桂柏，张熇．月球探测器技术［M］．北京：中国科学技术出版社，2007：127-130

Chu Guibai，Zhang He．Lunar probe technology［M］．Beijing：Chinese Science and Technology Press，2007：127-130（in Chinese）

［2］李海涛．深空导航无线电跟踪测量技术［M］．北京：清华大学出版社，2005：8-9

Li Haitao．Radiometric tracking techniques for deep space navigation［M］．Beijing：Tsinghua University Press，2005：8-9（in Chinese）

［3］Ondrasik V J，Curkendall D W．A first-order theory for use in investigating the information content contained in a few days of radio tracking data［R］．Pasadena，California：Jet Propulsion Laboratory，1971

［4］郝万宏，董光亮，李海涛．无线电干涉测量在深空航天器导航中的应用［J］．飞行器测控学报，2009，28（4）：1-7

Hao Wanhong，Dong Guangliang，Li Haitao．An introduction to application of radio interferometry in deep space navigation［J］．Journal of Spacecraft TT＆C Technology，2009，28（4）：1-7（in Chinese）

［5］Melbourne W G．Navigation between the planets［J］．Scientific American，1976，234（6）：58-74

［6］Berry D S，Border J S．CCSDS concept paper：Delta-DOR［R／OL］．［2012-03-01］．http：／／mailman．ccs-ds．org／piper-mail／sls-rn-g／attachments／20050811／67dfd381／delta-DOR-Concept-Paper．pdf

［7］Kikuchi F，Liu Q，Hanada H，et al．Pico-second accuracy VLBI of the two sub-satellites of SELENE（KAGUYA）using multi-frequency and same beam methods ［J］．Radio Science，2009，44（2）：doi：10．1029／2008RS003997

［8］Yu Zhijian，Dong Guangliang，Li Haitao，et al．Implementation of the ground TT＆C system for China’s Chang’e-1lunar exploration spacecraft［J］．Journal of Astronautics，2007，28（4）：1-3

［9］Thurman S W．Deep-space navigation with differenced data types，Part I：differenced range information content，TDA Progress Report 42-103［R］．Pasadena，California：Jet Propulsion Laboratory，1990

［10］Estefan J A，Thruman S W．Deep-space navigation with differenced data types，Part III：an expanded information content and sensitivity analysis，TDA Progress Report 42-109［R］．Pasadena，California：Jet Propulsion Laboratory，1992