一种基于Contourlet变换和SVD的数字水印算法

袁 莎，薛红月，赵 勇，周卫红

（云南民族大学数学与计算机科学学院,昆明 650500）

一种基于Contourlet变换和SVD的数字水印算法

袁 莎，薛红月，赵 勇，周卫红

（云南民族大学数学与计算机科学学院,昆明 650500）

为了提高水印的不可见性和抗旋转攻击性，在文献[1]的基础上提出了一种基于Contourlet变换和SVD结合的数字水印新算法.利用Contourlet变换的多方向性和各向异性的特点，将图像经Contourlet变换后，再对低频系数进行奇异值分解,随后将水印嵌入到奇异值矩阵,使水印具有较高的不可见性及较强的抗旋转攻击性。

Contourlet变换；SVD奇异值分解；数字水印；抗旋转

引言

数字水印技术是一种保护版权信息的有效手段.目前常用的水印方案分为空间域和变换域两大类，前者极具代表性的有最低有效位算法和回声掩蔽算法，该类算法操作简单、运算速度快，但嵌入量小，易遭攻击；变换域通过改变信号的变换域系数来进行水印嵌入,如DCT域水印算法、DWT域水印算法等，该类算法具有水印嵌入量大、透明性好等优点.随着小波理论与” 稀疏表达”的提出,人们将水印算法重点转向了小波域,但单纯的小波域算法由于其本身的不可平移性,使得纯小波算法面临几何旋转攻击时,水印提取图像严重失真.SVD奇异值矩阵的引入,使得抗几何旋转攻击能力得到加强.张仁昌，耿国华等人将小波变换与SVD分解相结合,提出了一种<基于奇异值分解和小波变换的抗几何失真数字水印新方法>[1],该算法对一般的图像处理操作及小角度的旋转攻击具有很好的鲁棒性,但对超过1度的旋转,提取水印保真性下降较大.本文在文献[1]的基础上提出了一种基于Contourlet变换和SVD结合的数字水印新算法,目的在于提高水印的抗几何旋转攻击能力.

1 算法的理论背景

1.1 Contourlet变换

小波理论的兴起，得益于对信号的时、频局部分析能力、对一维有界变差函数类的最优逼近以及多分辨分析概念的引入.由于二维小波是由一维小波张成的可分离小波，其只具有有限的方向，即水平、垂直、对角，方向性的缺乏使得小波变换不能充分利用图像本身的几何正则性.

文献[2]提出的Contourlet变换是2002年由M.N.Do和M.Vetterli在Curvelet变换的基础上，结合方向滤波的思想所提出的新的时频变换方法.Contourlet 变换将多尺度分析和方向分析分开进行，首先用拉普拉斯金字塔（LP,laplacianpyramid）变换进行多尺度分析捕获点奇异性，接着使用方向性滤波器组（DFB，directional filter bank）将分布在同一方向上的奇异点合成为一个系数，捕获高频分量（即方向性）.由于方向性滤波器本身不适合处理图像的低频部分，因此LP 的另外一个作用就是避免低频分量的“泄漏”（leaking）.LP和DFB 二者的结合，就构成了Contourlet 变换的核心，“塔式方向滤波器组”（PDFB，pyramidal di -rectional filter bank）.由于LP和DFB 具备完全重构特性，因此其组合PDFB 也必然能实现完全重构.由于LP 的冗余性，Contourlet 变换具有4/ 3的冗余度[3].

图（1）分别描述了小波与Contourlet的不同.

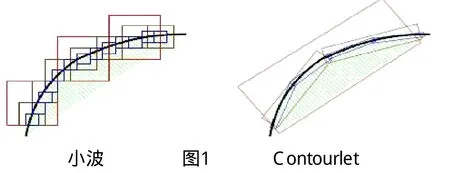
1.2 SVD奇异值分解

从线性代数的角度来说，一幅灰度图像是一个具有非零元素的矩阵.设定一幅灰度图像用字母I来表示,I∈RN*N,R表示实数域.那么，I的奇异值分解定义为：

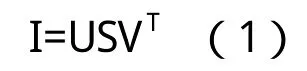
其中U，V∈RN*N两者都是酋矩阵，S∈RN*N是对角矩阵，其对角线上的元素满足：

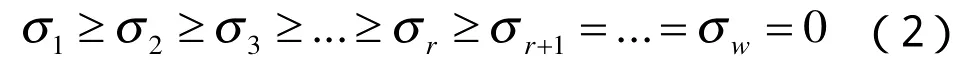
其中，r是S的秩，它等于非零奇异值的个数，σi是由该分解唯一确定的,叫作I的奇异值.

使用奇异值分解技术主要有以下三个方面的优势[4]:

1)奇异值分解对所要进行变换的矩阵的大小没有什么限制,可以是方阵也可以是长矩阵.

2)对于一般的图像处理,奇异值的稳健性非常好,不会有很大的变化.

3)奇异值反映的是图像内蕴特性而不是视觉特性,反映的是图像矩阵元素之间的关系.

2 本文算法设计思想

2.1 DWT-SVD水印算法

文献[1]提出了一种在小波域上通过对低频系数进行SVD奇异值分解，将水印嵌入到奇异值矩阵，从而达到嵌入水印的不可见性和鲁棒性.其嵌入及提取算法实现如下：

2.1.1 DWT-SVD水印嵌入算法

1）.读取原始灰度图像I，对I使用haar小波进行三层离散小波分解

2）.提取低频子带A，对其进行SVD奇异值分解：A=USV

3）.读取水印图像W，将W嵌入到奇异值矩阵S：S’=S+alpha*W，alpha为嵌入强度

4）.对S’再次进行奇异值分解，S’=U’S’V’,将S’替代S，与相应的酋矩阵重新构成低频子带A’=U*S’’*VT

5) .对重构的低频子带及其他的带通系数进行haar小波逆变换，得到嵌入水印后的图像

2.1.2 DWT-SVD水印提取算法

1) .读取原始灰度图像I以及嵌入水印后的图像I’,对这两幅图像同时使用haar小波进行三层离散小波分解

2) .提取两者的低频子带，分别记为A以及A’,分别对A以及A’进行SVD奇异值分解：

A=USV,A’=U’’S’’V’’

3) .记算矩阵S’=U’*S’’*V’T, 提取奇异值与嵌入水印前奇异值相减得到的水印信号:w’=(S’-S)/alpha

2.2 Contourlet-SVD 水印算法

对原始灰度图像进行Contourlet变换，选择低频子带做为嵌入对像，因为灰度图像的大部分能量集中于低频子带，低频子带能够满足人们视觉的要求，且对图像进行处理后对低频子带影响较小，从而增强了水印的鲁棒性.

本文在文献[1]的基础上，将其变换域由小波变为Contourlet域,将Contourlet变换结合SVD分解，利用SVD的特点，设计了对原始灰度图像过行Contourlet变换后的低频子带进行SVD分解，在奇异值矩阵上嵌入水印.

2.2.1 Contourlet-SVD 水印嵌入算法

1) .读取原始水印图像I，对I使用高通滤波及低通滤波均为’pkva’的Contourlet三层变换进行分解

2) .提取低频子带A，对其进行SVD奇异值分解：A=USV

3) .读取水印图像W，将W嵌入到奇异值矩阵S：S’=S+alpha*W,alpha为嵌入强度

4) .对S’再次进行奇异值分解，S’=U’S”V’,将S’’替代S，与相应的酋矩阵重新构成低频子带A’=U*S’’*VT

5) .对重构的低频子带及其他的带通系数进行Contourlet逆变换，得到嵌入水印后的图像

2.2.2 Contourlet-SVD 水印提取算法

1) .读取原始灰度图像I以及嵌入水印后的图像I’,对这两幅图像同时使用高通滤波及低通滤波均为’pkva’的三层Contourlet变换

2) .提取两者的低频子带，分别记为A以及A’,分别对A以及A’进行SVD奇异值分解：

3) .计算矩阵S’=U’*S’’*V’T, 提取奇异值与嵌入水印前奇异值相减得到的水印信号:w’=(S’-S)/alpha

由于奇异值矩阵具有一定的稳定性，在嵌入水印后对其进行一些微小操作并不会影响图像的重构，并且由于Contourlet变换具有各向异性和多分辨率的特性，使得该水印算法具有较强的鲁棒性和抗几何攻击性.

3 仿真实验结果及对比攻击性能比较

本文的实验平台为Matlab7.0,原始灰度图像采用512*512的Lena图像，水印图像采用64*64的Woman灰度图像，水印嵌入强度:alpha=0.2.经仿真发现，两种算法均能很好的生成含水印图像并顺利提取水印图像：

图2

为了客观的对DWT-SVD水印算法与Contourlet-SVD水印算法进行比较，我们引入峰值信噪比PSNR对两种算法进行评价：

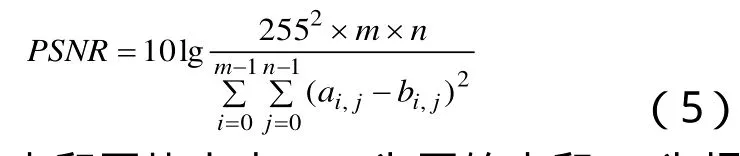
m×n为水印图片大小，ai,j为原始水印，为提取水印.

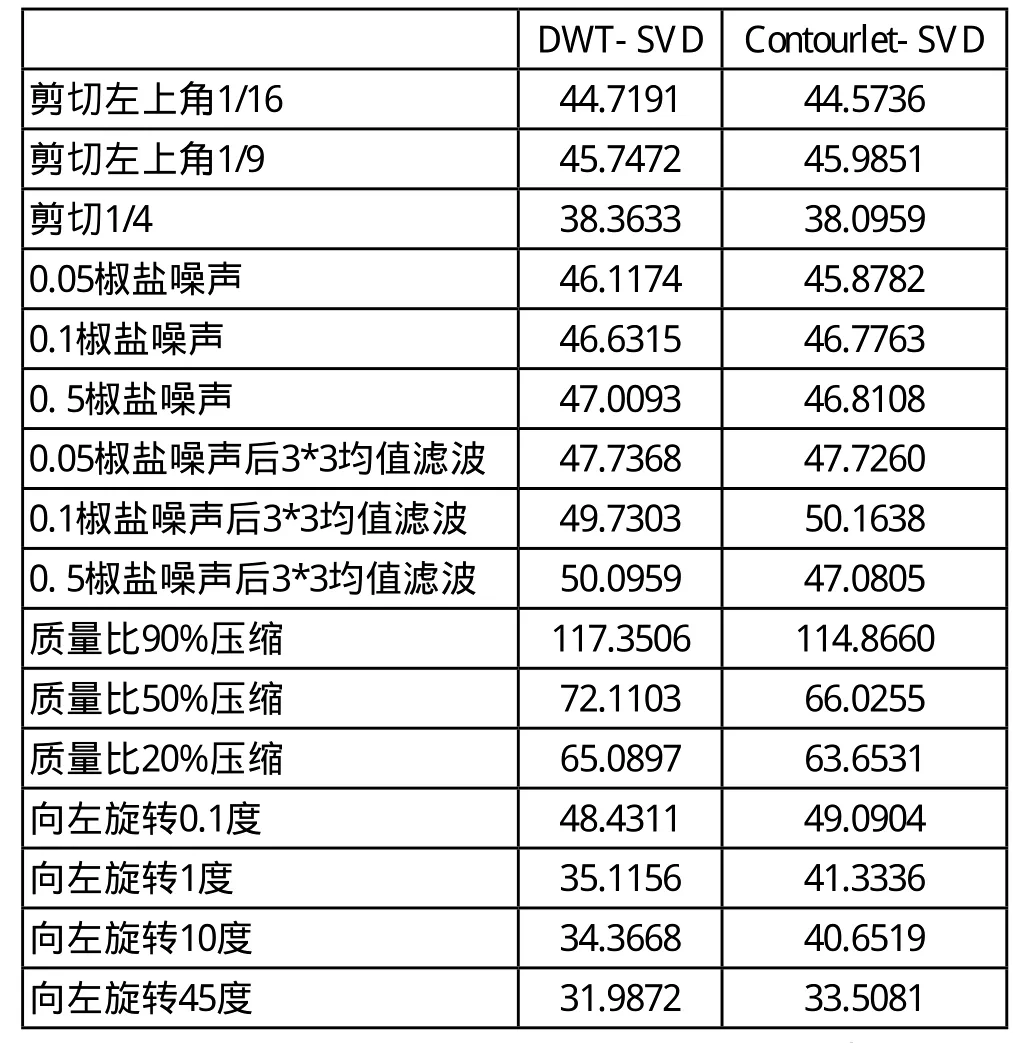
在未受攻击的情况下，DWT-SVD水印算法的原Lena图像与含水印Lena图像PSNR=106.0006db，水印提取PSNR=118.3590db；Contourlet-SVD水印算法的原Lena图像与含水印Lena图像PSNR=106.1502,水印提取PSNR=121.6406.在未受攻击时，Contourlet-SVD算法由于Contourlet变换的各向异性和多分辨率特性，使得含水印图像以及提取的水印具有较DWTSVD高的保真度.面对相同的鲁棒性攻击实验，两者对比如下：

?

通过上表可以看到，在加噪攻击、滤波情形下，Contourlet-SVD算法要略逊于DWT-SVD算法，特别是在压缩时，相差较大,如50%压缩时,文献[1]算法的PSNR值为72.1103,但本文算法为66.0255：这是由于Contourlet变换相比离散小波变换，其表达更”稀疏”,能量更集中,受奇异点位置影响较小波要大,奇异值反映的是元素间的关系,当图像受加噪、滤波攻击时,图像元素本身发生改变,奇异值有一定变化,Contourlet变换受影响较大.

但由于Contourlet具有多方向分解及各向异性的特点，其能真正体现对二维数据的逼近与稀疏表达,使得Contourlet-SVD算法在抗旋转攻击方面要优于DWT-SVD算法,如在旋转1度及10度时,文献[1]算法的PSNR值分别为35.1156和34.3668,本文算法值却分别为41.3336和40.6519.同时发现,当含水印图像仅仅是在相对元素位置及元素数量上发生改变时,如旋转,适量剪切攻击,此时元素间关系未发生明显变化,奇异值变化幅度较小,Contourlet变换受影响较小,此时该算法的保真性要大于小波变换算法.通过上述分析,可知本文算法在未受攻击及旋转攻击情形下水印的不可见性及鲁棒性方面要优于文献[1]的小波算法.

结束语

本文提出了一种基于Contourlet与SVD相结合的水印嵌入及提取算法，通过对图像进行Contourlet变换后，对低频子带进行奇异值分解，在奇异值矩阵上嵌入水印，利用奇异值矩阵的稳定性提高水印的不可见性和鲁棒性.通过以上仿真实验可知，在未受攻击时，Contourlet-SVD算法的保真性要优于DWTSVD算法，并且其在抗几何旋转主面同样优于DWTSVD算法.

[1] 张仁昌,耿国华.基于奇异值分解和小波变换的抗几何失真数字水印新方法[J].计算机应用与软件,2007,24(6).

[2] DO MN, VETTERLIM.Contourlets: a directional multiresolution image representation[A]//.Proceedings of 2002 International Conference on Image Processing.2002, 1: I-357-360.

[3] 陈开亮,王建军.一种HVS和Contourlet结合的图像水印算法.[J].计算机辅助设计与图形学学报 2007,6(19).

[5] 李海峰,宋巍巍,王树勋.基于Contourlet 变换的稳健性图像水印算法[J].通信学报 2006,27(4).

[6] 汤震浩,雍士华,马小虎.基于DWT和SVD的数字水印算法[J].电脑知识与技术 2009,5(25).

[7] 雍士华,马小虎.一种基于DWT和SVD的双重水印算法[J].南京师范大学学报(工程技术版) 2008,8(4).

[8] 鄢喜爱,常卫东,田华.数字水印技术及典型的攻击分析[J].太原师范学院学报(自然科学版) 2005,4(3).

[9] Huawei Tian, Yao Zhao, Rongrong Ni, Jeng-Shyang Pan.Geometrically Invariant Image Watermarking Using Scale-Invariant Feature Transform and K-Means Clustering[J].ICCCI(3) 2010 :47-55.

[10] Haohao Song_, Songyu Yu, Xiaokang Yang, Li Song, Chen Wang.Contourlet-based image adaptive watermarking[J].Signal Processing: Image Communication 23 (2008) 162178.

A Digital W atermarking Algorithm Based on Contourlet and SVD

YUAN Sha,XUE Hong-yue,ZHAO Yong,ZHOU Wei-hong
(School of Mathematics & Computer Science , Yunnan University of Nationalities,Kun Ming 650500,China)

For imropving the visibility and resistance of offensive attack, submitting a new dig ital watermarking algorithm based on Contourlet and SVD.Using traits of the Contourlet: change-mult idirect ions and anisotropy,use the Contourlet change to the image,singular value of low frequency component is decomposed,and then embed the watermarkimage into the singular decomposition matrix ,make the watermarkimage has more visibility,and resistance to the attack of offensive.

Contourlet change;SVD singular value decomposition;Digital wate rmarkimage;Resistance offensive

O24

A

1008-9128（2012）02-0032-04

2011-08-20

云南省教育科研基金项目（2011J049），云南民族大学青年基金项目（11QBQ08）

袁莎 (1987-)，女，在读硕士。研究方向为:图像处理与模式识别。

周卫红，男，副教授。

[责任编辑 张灿邦]