可观测量的电动机驱动电流建模①

黄飞超 陈明明 杨 戍

(1.兰州交通大学，甘肃兰州 730070;2.兰州理工大学，甘肃兰州 730050;3.华北科技学院基础部，北京东燕郊 101601)

可观测量的电动机驱动电流建模①

黄飞超1②陈明明2杨 戍3

(1.兰州交通大学，甘肃兰州 730070;2.兰州理工大学，甘肃兰州 730050;3.华北科技学院基础部，北京东燕郊 101601)

检验汽车行车制动器设计的优劣，需要得到电动机驱动电流与时间之间的精确关系。因为制动器性能的复杂性，驱动电流与时间之间的精确关系很难得到。基于模拟实验台，由能量等效转化的方法，将能量转化为可观测的转速以及对于转动物体来说恒定不变的转动惯量，建立了电动机驱动电流依赖于可观测量的数学模型。

驱动电流;转动惯量;制动扭矩

汽车的行车制动器连接在车轮上，它的作用是在行驶时使车辆减速或停止。但是检验制动器设计的优劣需要在各种不同的情况下进行大量的路试。由于在车辆设计阶段无法路试，故只能在专门的制动器试验台对所设计的路试进行模拟试验［1］。原则是试验台上的制动器的制动过程与路试车辆上制动器的制动过程尽可能一致，采用能量等效转化，将能量转化为可观测的、对于具体转动物体来说恒定不变的转动惯量。为了尽可能更好的去模拟实际过程，需要引入补偿的方法。

1 转动惯量求解

假设飞轮是对称匀质的空心圆柱体，设飞轮的转动惯量为J0。将飞轮等效为一个实心圆柱体，则其转动惯量JR，再将飞轮圆孔部分想象成实心圆柱体求出其转动惯量Jr，则有

下面建立求解对称匀质实心圆柱体转动惯量的模型:

设圆柱的密度为ρ，质量为m0，V为圆柱的体积，R0为圆柱半径，H为圆柱的高，θ为圆心角，Rx为圆柱上一块无限小的部分dv到圆心的距离，则对圆柱上任意一块无限小的部分dv其转动惯量为

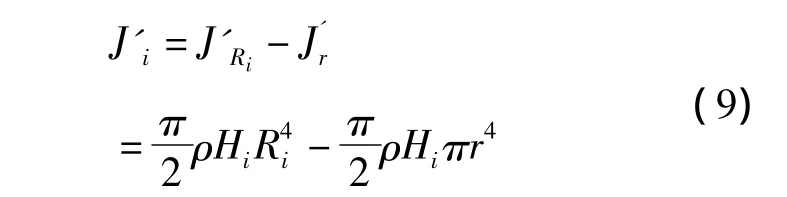
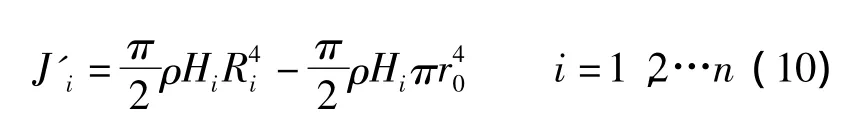
设试验台有n个飞轮，并且第i个飞轮外径Ri，内径r，厚度为 Hi转动惯量为这n个转动惯量与基础惯量Jb组合成机械惯量分别为 J1，J2…Jn，且 Ji=J'i+Jb。

假设电动机能补偿的能量相应的惯量的范围为［-e，e］Kg·m2，(e＞0)，组合机械惯量至少存在一个 JMI满足 J-e≤JMI≤J+e。并且，由于转轴半径应与飞轮内径相等即r0=r，有下式

此时电动机的补偿惯量为

2 建立电动机驱动电流依赖于可观测量的数学模型

制动过程中分为制动力恒定和非恒定两种情况讨论［2］。

2.1 制动力恒定的情况

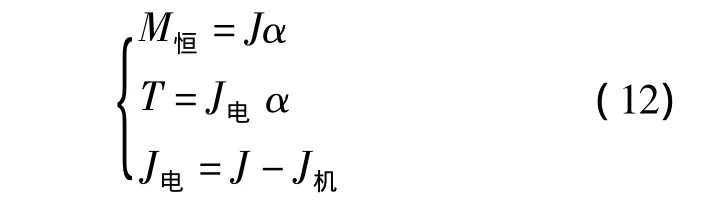
设试验台采用的电动机驱动电流与其产生的扭矩比例系数为K，则有

其中ω为转动物体的角速度，n为转动物体的转速，由(14)(15)可得

即为制动减速度恒定情况下电机驱动电流的表达式。

2.2 制动力非恒定的情况

制动力非恒定，则制动扭矩M非非恒定，角加速度也非恒定。此时有

假定在Δt内转速的变化是均匀变化的，则有

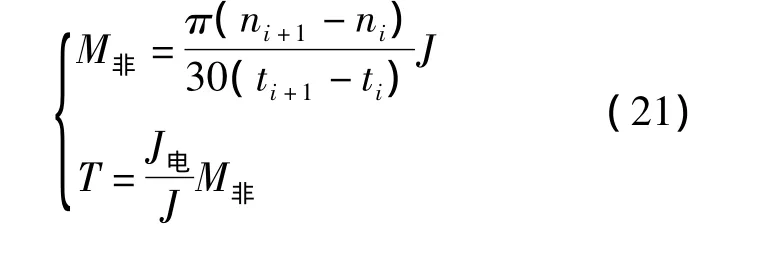
(23)式即为制动减速度非恒定情况下电机驱动电流的表达式，其中n、ni+1分别为第ti、ti+1时刻的转速。在非恒力的情况下，较短时间内的电流变化规律与恒力情况下是相同的，即

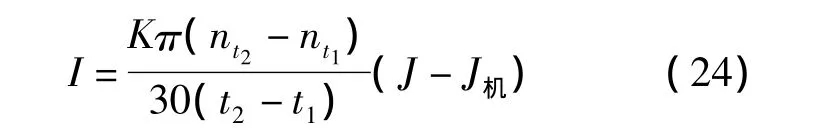
3 验证

路试模拟试验中，设车辆单个前轮的半径为0.286m，制动时承受的载荷为6230N，飞轮组由3个外直径1m、内直径0.2m的环形钢制飞轮组成，厚度分别为 0.0392m、0.0784m、0.1568m，钢材密度为7810Kg/m3，基础惯量为10Kg·m2，电动机能补偿的能量相应的惯量的范围为［-30，30］Kg·m2，假设制动减速度为常数，初始速度为50Km/h，制动5.0秒后车速为零。

由公式(4)得等效转动惯量为:J=52Kg·m2。

由公式(10)得三个飞轮的转动惯量分别为:30Kg·m2，60Kg·m2，120Kg·m2。

以上转动惯量可与基础惯量10Kg·m2组合成的机械惯量分别为:10Kg·m2，40Kg·m2，70Kg·m2，100Kg·m2，130Kg·m2，160Kg·m2，190Kg·m2，220Kg·m2。由于求得的等效转动惯量为52Kg·m2，电动机能补偿的能量相应的惯量的范围为［-30，30］Kg·m2，所以机械惯量可以选择40Kg·m2或70Kg·m2。因而补偿惯量以及电机驱动电流有以下两种情况:

1)当机械惯量选择40Kg·m2时，

由公式(11)得补偿惯量为:J补偿=12Kg·m2;

由公式(24)得驱动电流为:I=174.8A;

2)当机械惯量选择70Kg·m2时，由公式(11)得补偿惯量为:J补偿=-18Kg·m2;

由公式(24)得驱动电流为:I=-262.2A;

I＞0说明电机正转，I＜0说明电机反转。

由此得到的电动机驱动电流与时间之间的关系，设计控制系统时，将使输入电机的驱动电流处于动态调节中，得到最佳输入电流值，提高对电机的保护，使制动精确性和稳定性都能得到提高。［5］

［1］ 2009年高教社杯全国大学生数学建模竞赛题目A题《制动器试验台的控制方法分析》

［2］ 黄斐梨、王耀明、卢峻峰等.电动汽车永磁无刷电机驱动系统的仿真［J］.清华大学学报，1995，35(1):77-84

［3］ 张俊智、卢青春、黄海燕.发动机动态试验台的混合模拟研究［J］.清华大学学报，1999，39(8):60-63

［4］ 周品、何正风.MATLAB数值分析［M］.北京:机械工业出版社，2009

［5］ 周洪旋.制动器试验台电惯量系统控制方法研究［D］.吉林大学硕士学位论文，2005

The mathematical model of the motor drive current based on considerable measure

HUANG Feichao1，CHEN Mingming2，YANG Shu3

(1.Lanzhou University of traffic，Lanzhou Ganshu 730070;2.Lanzhou University Of Technology，Lanzhou Ganshu 730050;3.Department of Foundation，North China Institute of Science and Technology，Yanjiao Beijing-East101601)

In order to test the merits of the design on brakes，the precise relationship between the motor drive current and time is necessary.Because of the complexity of the Braking performance，it’s too difficult to get the precise relationship.On the basis of Energy Equivalent Conversion，this essay is to get the mathematical model based on the quantities of the motor，such as rotate speed and rotary inertia which is measurable or constant.

driving current;moment of inertia;braking torque

TM32

A

1672-7169(2012)01-0060-02

2011-12-13。基金项目:中央高校基本科研业务费资助(JCB1206B)。

黄飞超(1988-):男，陕西西安人，兰州交通大学硕士研究生，研究方向:智能控制。