二维欧氏空间中混杂构形的Möbius函数

江 娟，裴东河，陈志明

（东北师范大学数学与统计学院，吉林 长春 130024）

二维欧氏空间中混杂构形的Möbius函数

江 娟，裴东河，陈志明

（东北师范大学数学与统计学院，吉林 长春 130024）

研究了二维欧氏空间中一类新的混杂构形，即由直线构形和若干个圆组成的混杂构形，这是以往所研究的混杂构形的推广形式.并且利用Hasse图得到了此类混杂构形的相交偏序集的Möbius函数值公式.作为公式的应用，给出了两个具体的例子.

超平面构形；直线构形；混杂构形；Möbius函数

0 引言

超平面构形，一般简称为构形，是l维向量空间中余维数为1的子空间的有限集合.超平面构形这一与奇点理论有关的对象是20世纪70年代新兴的学科.Arnold，Brieskorn和Deligne三位大师都做过奠基性的工作.超平面构形不仅具有很好的代数、组合、拓扑性质，还在奇点理论、凸集几何、离散几何等数学分支上有着广泛的应用［1］.近年来，以Hiroaki Terao，Peter Orlik和Louis Solomon等人为代表的学者们在超平面构形领域取得了巨大的成果［2－9］.国内姜广峰、余建明等人在超平面构形的可约性及仿射Zariski对等方面也取得了重要的成果［10－12］.我们可以从多角度研究超平面构形，例如，文献［13-14］定义了类自由构形和球构形，给出了一类特殊的类自由构形和球构形的组合性质.文献［15］把构形和拟阵的关系具体化，讨论了一类特殊构形的超可解性.

胡毅第一次给出了混杂构形的概念，并研究了混杂构形的补空间的同调群［16］.根据胡毅的定义，苏丹和张敦穆构造了一类具体的混杂构形，给出了其特征多项式及房的个数公式［17］.吴栋研究了一类范围更广的混杂构形，得到了其Möbius函数值公式等组合与代数性质［18］.特征多项式是构形的一个重要的几何不变量，而构形的特征多项式与Möbius函数有着直接的关系.因此，构形的Möbius函数的研究是很必要的.

本文研究了R2中由直线构形和若干个圆构成的混杂构形，运用不同于文献［17-18］的方法，得到其Möbius函数值的计算公式.这为进一步研究Rn（n≥3）中的混杂构形提供了一种方法.

图1 混杂构形的类型

我们以二维欧氏空间为例，给出三个不同的混杂构形的例子，具体说明本文研究的混杂构形的特点.作为例子，图1中的（a），（b）分别为文献［17-18］中所研究的混杂构形，（c）则为本文所研究的混杂构形.文献［17-18］研究含有一个球面的混杂构形，本文所研究的混杂构形含有多个圆，是在二维情形下，对文献［17-18］所研究结果的部分补充.

本文中没有给出的定义及相关结论可参考文献［1，18］.

1 基本定义及定理

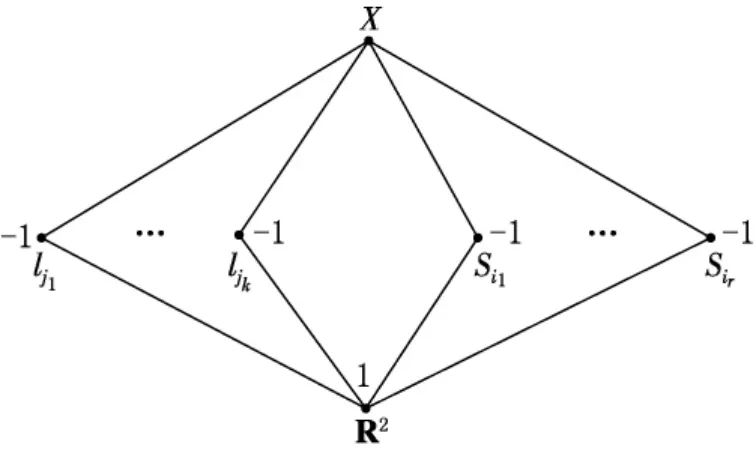
图2 相交偏序集L（~A）的Hasse图

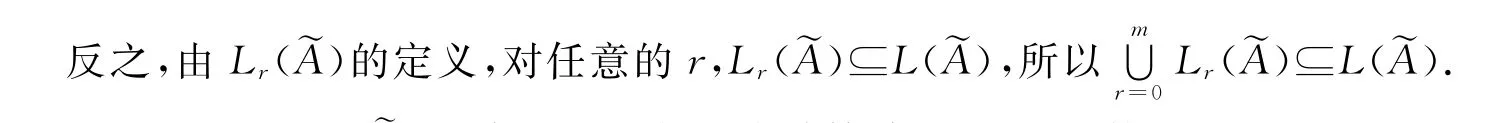
注1.2 文献［18］中，作者借助超平面构形的Möbius函数，得到了混杂构形的Möbius函数.本文定理1.1的证明中我们主要是应用Hasse图，获得了混杂构形的Möbius函数.在R2情况下，文献［18］中定理2.3.1是本定理的一个推论.

2 应用举例

下面我们给出定理1.1的具体应用.

例2.1 求图3中混杂构形的相交偏序集中点的Möbius函数值.

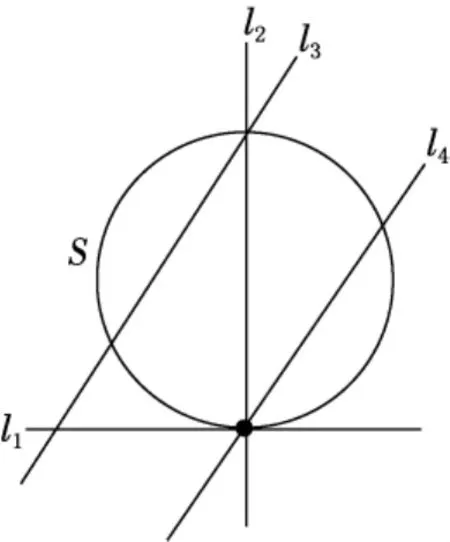
图3 单圆混杂构形

图4 多圆混杂构形

例2.2 求图4中混杂构形的相交偏序集中非横截相交点的Möbius函数值.

解 由图4可知，相交偏序集中有且仅有X＝l1∩l2∩l3∩S1∩S2一个非横截相交的交点.由定理1.1，μ（X）＝3＋2－1＝4.

事实上，我们可以继续研究Rn（n≥3）中的由超平面构形和若干个球面构成的混杂构形的Möbius函数，进而可以研究混杂构形的特征多项式，这为研究混杂构形的组合及其性质提供了一种方法.

［1］ ORLIK P，TERAO H.Arrangements of hyperplanes［M］.Berlin：Springer-Verlag，1992：1-325.

［2］ ORLIK P，SOLOMON L.Unitary reflection groups and cohomology［J］.Invent Math，1980，59：77-94.

［3］ ORLIK P，SOLOMON L.Combinatorics and topology of complements of hyperplanes［J］.Invent Math，1980，56：167-189.

［4］ TERAO H.Generalized exponents of a free arrangement of hyperplanes and Shephard-Todd-Brieskorn formula［J］.Invent Math，1981，63：159-179.

［5］ TERAO H.Multiderivations of Coxeter arrangements［J］.Invent Math，2002，148：659-674.

［6］ ABE T，TERAO H，WAKEFIELD M.The Euler multiplicity and addition-deletion theorems for multiarrangements［J］.J London Math Soc，2008，77：335-348.

［7］ ABE T，TERAO H.A primitive derivation and logarithmic differential forms of Coxeter arrangements［J］.Math Z，2010，264：813-828.

［8］ ABE T，TERAO H.The freeness of Shi-Catalan arrangements［J］.European J Combin，2011，32：1191-1198.

［9］ ABE T，TERAO H，WAKEFILED M.The characteristic polynomial of a multiarrangement［J］.Adv Math，2007，215：825-838.

［10］ JIANG G F，YU J M.Supersolvability of complementary signed-graphic hyperplane arrangements［J］.Australas J Combin，2004，30：261-274.

［11］ JIANG G F，YU J M.Reducibility of hyperplane arrangements［J］.Sci China Ser A：Mathematics，2007，50：689-697.

［12］ JIANG G F，YU J M.A Zariski pair in affine complex plane［J］.Asian J Math，2004，8：473-474.

［13］ 孟男，裴东河.类自由构形及其区域个数［J］.东北师大学报：自然科学版，2009，41（4）：13-15.

［14］ 崔秀鹏，裴东河，高瑞梅.球构形的分类及一类特殊球构形的特征多项式［J］.山东大学学报：理学版，2010，45（2）：59-62.

［15］ 孙志业，裴东河，高瑞梅.构形和拟阵的同构映射及关于超可解的几个性质［J］.山东大学学报：理学版，2009，44（1）：10-13.

［16］ HU Y.On the homology of complement of subspaces and spheres［J］.Proc Amer Math Soc，1994，122：285-290.

［17］ SU D，ZHANG D M.The characteristic polynomial of the mixed arrangement［J］.Wuhan Univ J Nat Sci，2007，12：203-206.

［18］ 吴栋.混合配置的组合与代数性质［D］.天津：南开大学组合数学中心，2009.

Möbius function of the mixed arrangement in two-dimensional Euclidean space

JIANG Juan，PEI Dong-he，CHEN Zhi-ming
（School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China）

Study on a new kind of mixed arrangements in two-dimensional Euclidean space，that is，the mixed arrangement which is composed of a line arrangement and several circles.These mixed arrangements are the generalizations of the former ones.By making use of Hasse diagram，the Möbius function value formula of the intersection poset of a mixed arrangement is obtained.As an application of this formula，two concrete examples are given.

hyperplane arrangement；line arrangement；mixed arrangement；Möbius function

O 157.3

110·77

A

1000-1832（2012）02-0001-04

2011-05-12

国家自然科学基金资助项目（10871035）.

江娟（1986—），女，硕士，主要从事超平面构形的组合性质研究；通讯作者：裴东河（1964—），男，博士，教授，博士研究生导师，主要从事奇点理论和超平面构形研究.

陶 理）