分形理论在吉林省交通网络研究中的应用
2012-09-25李秀玲李诚固
李秀玲,李诚固
(1.吉林财经大学应用数学学院,吉林长春130117;2.东北师范大学城市与环境科学学院,吉林长春130024)
分形理论在吉林省交通网络研究中的应用
李秀玲1,李诚固2
(1.吉林财经大学应用数学学院,吉林长春130117;2.东北师范大学城市与环境科学学院,吉林长春130024)
运用分形理论,对吉林省的交通网络进行了定量分析.通过计算盒子维数和空间关联维数,分析了其网络覆盖形态及空间分布特征.结果表明:吉林省交通网络具有明显的分形特征,发育较为成熟,整体通达性较好,应充分利用发达的交通网络带动经济的发展.
交通网络;覆盖形态;空间分布;分形
交通作为联系地理空间中社会经济活动的纽带,是社会化分工成立的根本保证.交通网络作为城市地理空间系统的一个子系统,实现着城市人流、物流的有效流动和运转,是城市繁荣有序的根源和发展能力的象征,因此城市的发展离不开交通网络的发展和完善.交通网络的建设与区域经济的发展是互相融合、相辅相成的.一个区域的交通发展,常伴随而来的是经济发展的提速[1].
交通便捷程度主要取决于交通网络的完善程度,交通网络的完善程度可以用密度和结构来表述.在其他条件不变的情况下,交通网络密度越大,交通越便利.但是,并不是交通网络密度大的地方交通就一定便利.Braess佯谬指出,有时增加了交通道路反而降低了通达能力,甚至引起城市与区域的交通阻塞[2].衡量交通便捷程度还要考虑到交通网络的结构,即要综合考虑联结度和通达度指标[3].通常情况下,交通网络密度大,联接度高、通达度好的网络是完善的交通网络.
交通网络的完善程度通常直接影响到一个区域的地理可进入性.区域的绝对地理位置是固定不变的,但是随着交通条件的变化,其相对地理位置会发生变化,可达性也会随之发生巨大的变化.交通便利性的提高意味着对外交往可能性的提高,无论是针对原料产地、生产地还是消费地而言,都会促进经济活动的发展,从而成为吸引经济活动布局的重要因素[3].交通网络发展的研究对区域发展具有重要的实践与指导意义,研究区域范围越大,越能反映出交通网络发展的全面性.
分形理论[4]是由美籍法国数学家B.B.Mandelbrot创建的,1977年他发表的专著《分形:形状、机遇和维数》标志着分形几何学的诞生.B.B.Mandelbrot将分形定义为其组成部分和整体存在某种自相似性的几何体,它破碎而复杂,是不规则和不可微的,因此不能用传统的欧几里得几何来研究.分形体的自相似性,指的是统计意义上的自相似,而不是数学意义上的自相似.
对分形体进行定量研究,需要对分形维数进行分析.分形维数,简称为分维或分数维,它既可以是整数也可以是分数.维数分析是分形理论的精华所在,通过对分维的分析来反映局部对整体的填充能力,揭示系统的演化机理.本文通过计算交通网络覆盖度和空间关联维数对吉林省交通网络结构进行了研究,以揭示其交通网络分形特征.这些分形维数能够反映交通网络的适应性、通达性、可达性,体现交通网络的空间形态分布特征,在区域问题研究中能够有效开展空间研究.
1 城市交通网络的分形研究
1.1 交通网络覆盖形态
将边长为R的网格覆盖研究区域,用N(R)表示有交通线路通过的网格数.当R变化时,N(R)也随着变化.若交通网络空间分布是分形的,则有

式中:D表示交通网络覆盖度,反映网络覆盖形态.为了说明其实际意义,我们将(1)式变为

采用差分代替微分,得到

式中:Ri表示第i次细分网络后的网格边长;N(Ri)表示第i次细分网络后有交通线路通过的网格数.现在取单个小正方形来说明,假设此正方形中有交通线路通过,当它被划分为4个小的正方形时,容易算得:当4个小正方形中均有交通线路通过时,D=2;当其中3个小正方形有交通线路通过时,D=1.585;当其中有2个小正方形有交通线路通过时,D=1;而只有1个小正方形有交通线路通过时,D=0.由此可知,分维数在是否有交通线路通过的意义上反映出新网络与原网络的相似程度.当D=2时,具有完全的自我相似性.分维数越大,网络中有线路通过的网格数越多,网络的覆盖形态就越好[5].通常为了使道路覆盖率较高,让全区域基本都有道路通过,在路网规划中取值为1.585≤D≤2.当分维值在1.585与2之间取值时,交通网络具有基本覆盖的相似特性.
由(2)式计算分维数D(Ri),(Ri,D(Ri))将形成一条曲线,这条曲线用来描述覆盖度随网格边长变化的关系,称其为覆盖度曲线.在这条曲线上,相对于D(R*)≥1.585的临界值R*称为交通网络的覆盖深度.它表示,当网络中平均有约3/4的区域内有线路通过时的最小网格边长.覆盖深度越小,说明相距较小的距离就有一条线路,因此交通状况就越好[5].
1.2 交通网络空间相关性
定义空间关联函数为:
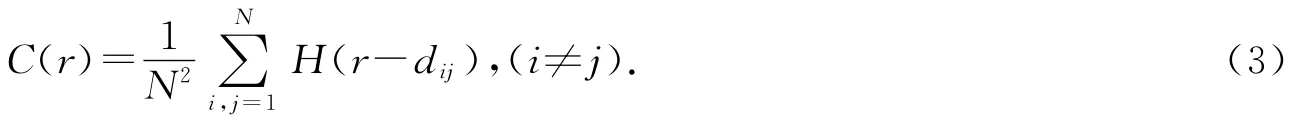
式中:r为码尺;dij为i,j两城市的距离;H为Heaviside函数

在具体计算过程中,为了计算方便,通常将(3)式改为:
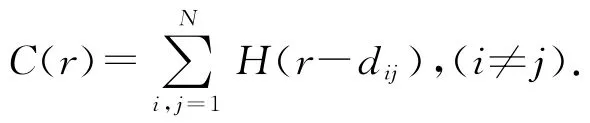
如果研究对象的空间分布是分形的,则应具有标度不变性,即

由(5)式易知

若dij为i,j两城市的欧氏距离,即乌鸦距离,则D为城市体系的空间关联维数;若dij为i,j两城市的实际交通距离,即乳牛距离,则D为交通网络的关联维数.为了区分这两个维数,我们将交通网络的关联维数记为D′.通常D′越接近于D,意味着城市间的连通性就越好.空间关联维数能够有效地反映城市体系中城市之间交通网络的通达性和城市之间的关联程度.刘继生等进一步定义牛鸦维数比为

牛鸦维数比是衡量城市体系交通网络通达性的定量指标,当ρ>1时,意味着交通网络的通达性较差;而ρ越接近于1,说明城市体系中城市间越接近于直线式连通,交通网络的通达性越好,城市之间的关联程度也就越高;当ρ=1时,意味着交通不受任何限制,但是这种极端理想的状况在现实社会中一般是不存在的[6].
2 吉林省交通网络的分形特征
2.1 研究区域情况
吉林省位于我国东北地区的中部,地处北温带,地理位置为东经121°38′~131°19′、北纬40°52′~46°18′.全境东西最长约750km,南北最宽约600km,总面积18.74万km2,约占全国总面积的2%,居全国第14位.吉林省现有8个地级市、1个自治州、20个县级市、17个县、3个自治县[7].吉林省的交通以铁路为主、公路为辅.铁路以长春为中心,以吉林、四平、梅河口为主要枢纽,有京哈、长图、长白、四齐、沈吉、四梅、梅集等铁路干线,形成了连接市州及城乡的铁路网络.公路建设发展较快,有长春至吉林、营城子,延吉至图们江,长春绕城和途经长春的京哈高速公路,吉林至延吉和图们江至珲春高速公路.
2.2 吉林省交通网络覆盖形态分维测算
用边长为R的网格覆盖吉林省交通地图,计算有交通线路通过的网格数N(R).改变网格边长R,得到点对(R,N(R)),首先我们在坐标系中将(R,N(R))作双对数坐标图(见图1),然后利用SPSS进行模拟计算,得到

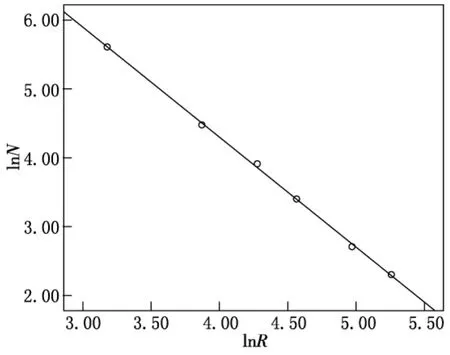
图1 交通网络覆盖形态分形维数双对数坐标图
相关系数R=0.999,即覆盖度D=1.598.再利用式(2)计算D(Ri),(Ri,D(Ri))形成一条曲线,该曲线近似地呈线性形状(见图2),利用线性回归分析法进行模拟计算,可得

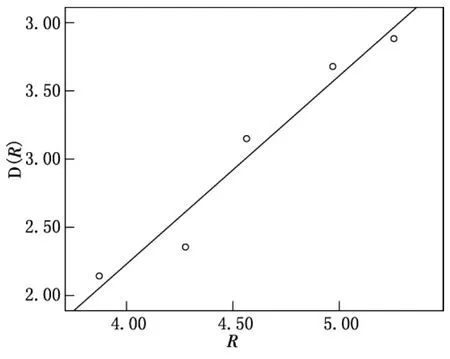
图2 覆盖度拟合直线图
相关系数R=0.976.在α=0.005下,Rα=0.974,R>Rα,故两变量间线性相关关系显著.统计量F=60.955,在显著性水平α=0.005下,Fα=55.55,F>Fα,故该回归方程的回归效果显著.令D=1.585,代入式(8)可得覆盖深度
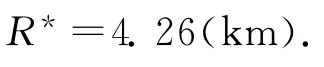
吉林省交通网络覆盖度D=1.598>1.585,网络覆盖形态较好.相距约4.26km的距离就有一条交通线路.
2.3 吉林省交通网络空间关联维数测算
下面分析吉林省交通网络的空间分布情况.借助于吉林省交通地图得到表1和表2,表1为吉林省9个主要城市之间的直线距离,表2为交通距离,这两个表中的空白处可以由右上方的数据对应得到.用步长Δr=50km作为距离标度r,得到点对(r,C(r)),然后在坐标系中我们将(r,C(r))作双对数图(见图3),再利用SPSS进行模拟计算,分别得到
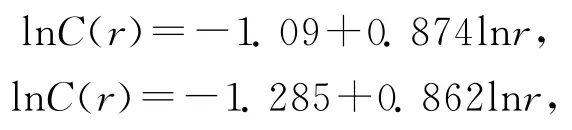
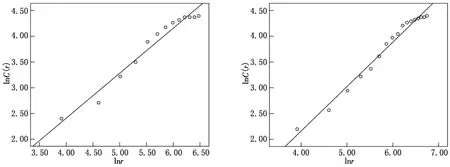
图3 吉林省城市和交通网络空间分布的双对数坐标图

表1 吉林省两两城镇间直线距离-乌鸦距离阵km

表2 吉林省两两城镇间交通距离-乳牛距离阵km
相关系数分别为R=0.982和R=0.991,即城市体系空间关联维数D=0.874,交通网络的关联维数D′=0.862,由此可以得到吉林省交通网络的牛鸦维数比为ρ=0.9863.ρ低于并接近于1,说明吉林省的交通网络整体通达性比较好,发育比较成熟.
3 结论
(1)分维测算的相关系数高达0.999和0.991,说明吉林省交通网络具有非常明显的分形特征,分形理论适合于吉林省交通网络的测算分析.
(2)在东北地区,吉林省位于黑龙江省和辽宁省之间,是东北地区的主要交通枢纽,吉林省的铁路、公路、管道运输在全国也占有重要的地位.吉林省交通网络发育比较成熟,通达性比较好,从而为东北地区乡村与城市、生产与消费、产品与市场之间架起了桥梁,为工业原料及商品运输提供了快捷的服务,也为乡村人口向城市迁移提供了条件,同时强化了产业的城市选择以及城市的产业吸引.
(3)长春市和吉林市是吉林省中部地区的两个特大城市,长吉高速公路建成后,这两个城市之间仅相距112km,因此在发挥这两个城市之间距离优势的基础之上,在产业、基础设施建设、生态环境整治方面力争资源共享,避免资源浪费,两个城市争取在资源开发和产品结构上形成自己的特色,避免同类项目低水平重复建设,通过长吉一体化发展,对我省的经济发展起到更加突出和明显的辐射及带动作用.
(4)长白山、北大湖、松花湖、查干湖、净月潭、向海草原等是吉林省著名的旅游胜地,在未来的城市旅游业发展中要充分利用发达的交通运输网络,进一步发挥这些旅游区的生态环境优势,提高它们的对外旅游吸引力,从而提高我省的经济收入,带动我省经济的发展.
(5)交通网络建设引起的生态环境问题日益严重,因此在交通网络规划中必须重视减少污染、保护环境与提高土地利用等问题.
[1] 杜德斌,黄吉乔.长江三角洲城市带一体化的交通网络模式构[J].经济地理,1999,19(3):91-95.
[2] BRAESS D.A paradox on traffic networks[EB/OL].http://homepage.ruhr-uni-bochum.de/.2004.
[3] 李小建.经济地理学[M].高等教育出版社,2006.
[4] MANDELBERT B B.Fractal:from,chance and dimensions[M].New York:W H Freeman,1977.
[5] 丁以中,楼勇.分形理论在交通运输网络评价中的应用[J].上海海运学院学报,1998,19(4):7-12.
[6] 刘继生,陈彦光.城镇体系空间结构的分形维数及其测算方法[J].地理研究,1999,18(2);171-178.
[7] 李秀玲,李诚固.基于分形理论的吉林省城市体系空间结构特征研究[J].东北师大学报:自然科学版,2009,41(4):145-148.
Abstract:The spatial structure of Jilin Province was quantitatively analysed using the fractal theory.The box-counting dimension and the spatial correlation dimension was put forward to analyzes the covering formation of transportation network and spatial distribution characteristics.And it also shows that transportation network of Jilin Province has the fractal characteristics,it developed maturely,the whole system of transportation network is much better.It should use develops transportation network to improve economic development.
Keywords:transportation network;covering formation;spatial distribution;fractal theory
(责任编辑:方 林)
The application of the fractal theory on study of the transportation network in Jilin Province
LI Xiu-ling1,LI Cheng-gu2
(1.School of Applied Mathematics,Jilin University of Finance and Economics,Changchun 130117,China;2.College of Urban and Environmental Sciences,Northeast Normal University,Changchun 130024,China)
K901;F 503[学科代码]170·4520
A
2012-01-23
国家自然科学基金资助项目(40471014);吉林省自然科学基金资助项目(201115183).
李秀玲(1973—),女,博士,副教授,主要从事应用数学和区域经济学研究;李诚固(1960—),男,博士,教授,博士研究生导师,主要从事城市规划和区域经济学研究.
1000-1832(2012)02-0138-05
