一种拦截机动目标的最优中制导律设计
2012-12-25周池军雷虎民叶继坤
周池军,雷虎民,叶继坤
(空军工程大学 导弹学院,陕西 三原713800)
对于中远程地空导弹,为了提高导弹的制导精度和射程,需要采用二级以上的复合制导模式.其中中制导的任务是把导弹导引到末制导导引头能够截获目标的有利空间,保证主动雷达导引头可靠截获目标,并尽可能地为末制导段提供一个良好的初始攻击条件,如航向误差要小,动能要大等[1,2].文献[3]在最优预测中制导律的基础上,设计了一种导弹在交班时刻性能最优的中制导律,使导弹在交班点处速度达到最大,导弹与目标的相对几何关系达到最佳.但所提出的中制导律需要对命中点以及交班点进行预测,预测的精度对制导律的影响较大.文献[4]针对大气层外中段拦截问题,设计了一种带有固定推进时间的近最优中制导策略,充分考虑了两飞行器之间重力差的影响,但没有对交班时刻的角度进行约束,而且需要利用变系数线性微分方程来求解最优制导律,推导过程较为复杂.文献[5]通过引入伪控制变量的概念,针对低速目标设计了一种最优末制导律,该制导律推导过程简单,但攻击高速大机动目标时,剩余飞行时间估计误差较大,这严重影响了导弹的制导性能.
为克服以往中制导律推导过程的复杂性,本文以最优控制理论为基础,将最小化控制能量和交班时刻速度前置角作为性能指标,利用伪控制变量将变系数线性微分方程转化为常系数线性微分方程,设计了一种最优中制导律,并通过仿真验证了该制导律的有效性.
1 弹目相对运动模型
为了便于研究导弹的中制导律,假设导弹在飞行过程中不发生滚转,将导弹在三维空间中的运动解耦成纵向平面和侧向平面,并分别进行研究.由于侧向平面的运动与纵向平面的运动类似,本文仅针对纵向平面拦截情况进行分析.纵向平面内的弹目相对运动关系如图1所示.

图1 弹目相对运动关系
图1中vm,vt分别为导弹和目标的速度;am,at分别为导弹和目标的法向加速度,它们分别垂直于各自的速度矢量,只改变速度的方向,不改变速度的大小;θm,θt分别为导弹和目标的弹道倾角;ηm和ηt分别为导弹和目标的速度前置角;R为弹目相对距离,q为弹目视线角.弹目相对运动学模型为

式中,ηm=q-θm,ηt=q-θt.对式(2)求导,并将式(1)代入,整理得:

2 最优制导律的设计
中远程地空导弹中末制导交班点处的角度约束是导引头成功捕获目标的关键.在交班点处希望导引头敏感轴指向目标,可以通过调整俯仰角ϑ间接调整导引头指向.直接控制ϑ不易实现,由于在中制导段导弹过载较小,攻角α很小,可近似认为θm=ϑ.因此,只要在交班时刻使弹轴指向目标,即θm=q,就可以认为导引头能够以最佳的角度捕获目标,并为末制导提供最优的初始条件[6].
设导弹的控制量为法向过载,即

选取x1=ηm,x2=为状态变量,将导弹的法向过载作为输入量,则弹目相对运动的状态空间描述为

式中,
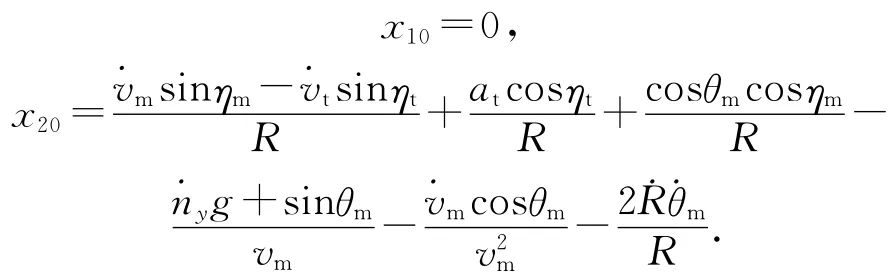
式(7)为变系数线性微分方程,直接求解是十分困难的,因此,引入一个伪控制变量:

则弹目相对运动可描述为

考虑控制能量和交班时刻的角度约束2个因素,选取性能指标函数为[7]


式中,X*(t)为控制量取最优时所对应的系统状态,P(t)为半正定对称矩阵,且满足黎卡提方程:

求解P(t)可得:

式中,

剩余飞行时间tgo=tf-t0.
对于中制导律而言,在中末制导交班时刻,导弹弹轴对准目标即认为此时导引头达到捕获目标的最佳几何位置,因此约束条件为x1(tf)=0,ηm(tf)=0,故取f1→∞,而对导弹的速度前置角变化率不作约束,取f2=0.代入式(13)得:
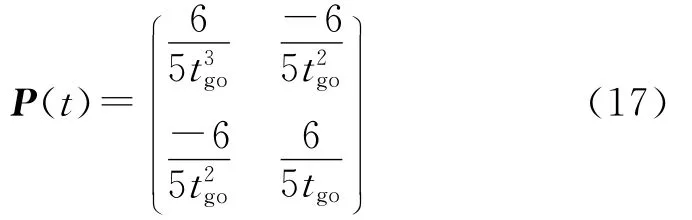
由式(11)、式(17)可得:

将式(18)代入式(8)得导弹的法向过载ny满足:

式中,

3 制导律的实现
3.1 制导信息的获取
由制导律的形式可知,要求解最优制导律,需要用到的信息包括导弹信息、目标信息以及弹目相对运动信息3类.导弹的运动信息可以通过自身的捷联惯测装置解算得到.对于处在中制导段飞行的导弹,导引头尚未开机,制导所需的目标信息以及弹目相对运动信息均由地面雷达测量或计算得到,并实时传递给导弹.地面雷达可以直接测量目标与雷达连线的视线高低角、目标接近雷达的速度以及目标与雷达之间的距离等信息,通过滤波装置可以计算视线高低角速度以及目标接近雷达的速度的导数,根据目标和雷达的相对运动关系可以解算得到目标的速度、法向和切向加速度以及弹道倾角等实时运动信息.同时,地面雷达结合导弹的运动可以计算得到弹目相对运动信息.由于地面雷达具有强大的信息处理能力,因此,测量或计算得到的目标信息和弹目相对运动信息的精度完全可以满足中制导需求.
3.2 剩余时间的估计
剩余时间的估计算法很多,常见的算法都是利用弹目相对距离和弹目相对距离变化率进行估计[3,5].对于固定目标和低速目标,这种算法估计的剩余时间较为精确,但是对于大机动目标,估计的误差较大.这里,给出一种新的剩余时间估计算法.
当目标不机动时,由弹目相对距离和弹目相对距离变化率可得:

当目标进行机动时,由弹目相对运动关系可得:

式中,vm,los,vt,los分别为导弹、目标速度在弹目视线方向上的分量;am,los,at,los分别为导弹、目标法向加速度在弹目视线方向上的分量.由式(21)可得:

式中,I=am,los-at,los,H=vm,los-vt,los,K=-R.求解式(22)可得:

式中,Δ=H2-4IK,tgo按下列规则进行取值:
①当Δ<0 或 者am,los,at,los同 时 为 0 时,tgo=tgo,0;
②当Δ≥0且|tgo,1-tgo,0|<|tgo,2-tgo,0|时,tgo=tgo,1;
③当Δ≥0且|tgo,1-tgo,0|>|tgo,2-tgo,0|时,tgo=tgo,2.
4 仿真分析
假设目标作超声速蛇形机动,初始时刻目标的位置为(50km,10km),速度vt=800m/s,切向加速度t=-gsinθt,法向加速度at=6gsin(0.4t),目标的初始弹道倾角为180°.导弹中制导初始时刻的位置(2km,1km),速度vm=900m/s,切向加速度m=-gsinθm,初始时刻弹道倾角为21°,雷达导引头的锁定距离为12km.
考虑制导系统延迟,将导弹的自动驾驶仪传递函数T等效为一个惯性环节和一个振荡环节的串联模型,可以表示为[8]式中,自动驾驶仪时间常数τ=0.5s,阻尼常数ζ=0.6,频率ωn=18rad/s.

为了体现本文所设计的最优中制导律(OGL)的制导效果,将其与带角度约束的变结构制导律(VSG)[6]和修正比例导引律(APN)[9]进行比较.
为比较中制导过程中的能量消耗,采用控制能量[8](Ec)作为比较参数,其计算形式为仿真结果如图2~图6及表1所示.


图2 导弹与目标运动轨迹

图3 前置角变化曲线
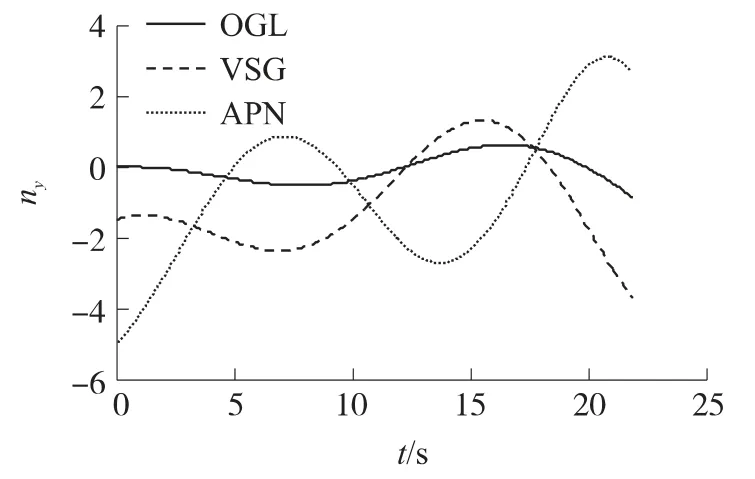
图4 制导指令变化曲线

图5 视线角速度变化曲线

图6 剩余时间变化曲线

表1 拦截参数比较
由图2可知,采用最优制导律得到的弹道比采用变结构制导律和修正比例导引律得出的弹道更加平滑.由图3可知,3种制导律在中末制导交班时刻均能得到较小的速度前置角,但采用最优制导律时,导弹在中末制导交班时刻的速度前置角几乎为0,可以认为导引头已经达到捕获目标的最佳几何位置.由图4可知,采用最优中制导律时,导弹的法向过载较小,受目标机动的影响较小,而采用变结构制导律和修正比例导引律时,在初始时刻和中末制导交班时刻导弹的制导指令较大.从图5可知,采用最优中制导律时,视线角速度的变化相比其它2种制导律更加平稳,中制导结束时刻,视线角速度较小.由图6可知,与传统的剩余时间计算方法相比,基于本文提出的计算方法得到的剩余时间更能体现目标的运动特性,2种计算方法得出的剩余时间的偏差随着弹目距离的减小而逐渐减小,在中制导末段2种计算方法得出的剩余时间几乎一致.从表1可以看出,采用最优中制导律时导弹在中末制导交班点处的过载和速度前置角均很小,能够保证导引头成功捕获目标以及中末制导弹道的平滑过渡,整个中制导过程消耗的能量很小,虽然中制导时间稍有增加,但相对于变结构制导律和比例导引律仍然具有明显的优势.
5 结束语
本文以控制能量和中末制导交班时刻导弹的速度前置角为性能指标,利用伪控制量简化了制导规律的求解,得出了一种最优中制导律.仿真结果表明,该最优中制导律能够有效地保证中末制导的顺利交班,并为末制导提供良好的初始攻击条件.本文在最优中制导律的设计过程中,没有考虑通过滤波或估计得到的目标信息和弹目相对运动信息的误差.采用先进的滤波算法减小误差并分析误差对制导精度的影响是下一步需要研究和解决的问题.
[1]OZA H B.A nonlinear suboptimal guidance law with 3Dimpact angle constraints for ground targets[C].AIAA Guidance,Navigation,and Control Conference.Toronto:AIAA,2010:8 185-8 210.
[2]王玉林,周绍磊,雷明.超声速拦射导弹的一种预测变结构中制导律[J].飞行力学,2009,27(5):47-50.WANG Yu-lin,ZHOU Shao-lei,LEI Ming.Forecast variable structure midcourse guidance law design for supersonic intercept missile[J].Flight Dynamics,2009,27(5):47-50.(in Chinese)
[3]董朝阳,周雨.一种交班时刻性能最优的中制导律设计与仿真[J].系统仿真学报,2009,21(24):7 873-7 877.DONG Chao-yang,ZHOU Yu.Design and simulation of han-dover performance optimal midcourse guidance law[J].Journal of System Simulation,2009,21(24):7 873-7 877.(in Chinese)
[4]郑立伟,荆武兴.大气层外拦截器近最优中制导律设计[J].宇航学报,2008,29(1):229-235.ZHENG Li-wei,JING Wu-xing.Design of a near optimal midcourse guidance law for exoatmospheric interceptor[J].Journal of Astronautics,2008,29(1):229-235.(in Chinese)
[5]冯志刚,杨希祥.反舰导弹最优末制导及其仿真研究[J].弹箭与制导学报,2006,27(2):39-41.FENG Zhi-gang,YANG Xi-xiang.Research on optimal terminal guidance law for anti-ship missile and its simulation[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,27(2):39-41.(in Chinese)
[6]周绍磊,雷明,戴邵武,等.用于复合制导的变结构中制导律研究[J].弹箭与制导学报,2008,28(5):11-13.ZHOU Shao-lei,LEI Ming,DAI Shao-wu,et al.An investigation of variable structure midcourse guidance law applied to combined guidance[J].Journal of Projectiles,Rockets,Missiles and Guidance,2008,28(5):11-13.(in Chinese)
[7]RYOO C K,CHO H.Optimal guidance laws with terminal impact angle constraint[J].Journal of Guidance,Control and Dynamics,2005,28(4):724-732.
[8]SRIVASTAVA R,PRABHAKAR N.Three dimensional nonlinear inverse dynamics guidance law for parallel navigation[C].AIAA Guidance,Navigation,and Control Conference and Exhibit.Rhode,Island:AIAA,2004:4 904-4 911.
[9]李朝旭,郭军,李雪松.带有碰撞角约束的三维纯比例导引律研究[J].电光与控制,2009,16(5):9-12.LI Chao-xu,GUO Jun,LI Xue-song.Study on three-dimensional PPN with impact angle constraints[J].Electronics Optics &Control,2009,16(5):9-12.(in Chinese)
