助推－滑翔导弹弹道优化与总体参数分析

刘 欣，杨 涛，张青斌

（国防科学技术大学 航天与材料工程学院，长沙410073）

助推－滑翔导弹通过火箭助推加速，依靠滑翔弹头的高升阻比外形，利用空气动力控制飞行轨迹，实现远距离的非弹道式再入机动飞行.与弹道导弹相比，由于其在增大射程、突防、再入段机动等方面具有优势，助推－滑翔导弹逐渐成为近来的研究热点[1].

弹道优化设计是助推－滑翔导弹总体设计的关键技术之一.助推－滑翔导弹的弹道可初步分为主动段、自由飞行段、再入段，目前国内外相关研究集中在滑翔弹头再入弹道优化设计方面，针对导弹全弹道优化的研究较少.文献[2]利用近似方法对全球到达高超声速飞行器的弹道特性进行了分析，文献[3]利用序列二次规划法对助推－滑翔导弹纵向全弹道进行最大射程优化.由于助推－滑翔导弹弹道的复杂性，利用解析法进行总体参数分析十分困难，且误差很大，结合各种优化技术对助推－滑翔导弹的弹道特性与总体参数进行分析是一种趋势.

本文利用Gauss伪谱法对全弹道进行优化设计，并分析了起飞质量、主动段终端倾角等参数对导弹射程的影响.

1 助推器参数估算

为了完成主动段弹道的计算，建立起飞质量与主动段终点参数乃至导弹射程的联系，需要对助推器的基本参数进行估算.

假设助推－滑翔导弹采用单级固体火箭助推.若初始速度为零，根据齐奥尔柯夫斯基公式，单级火箭的理想速度增量为[4]

式中：u′e为有效排气速度，数值上等于真空比冲Ip；mf为载荷质量，m0为火箭起飞质量，m0－mf为助推器质量；结构系数ε为助推器结构质量与助推器质量之比.考虑飞行过程中由引力、气动力和大气静压引起的飞行器速度损失Δv，则要使火箭主动段终点速度达到vf，火箭的理想速度增量应为vid＝vf＋Δv，可求得起飞质量与目标速度、载荷质量的关系：

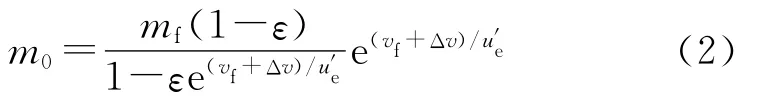
依据文献[5]中的相关论述，可取u′e＝Ip＝2 800m/s，ε＝0.1，Δv＝0.2vf.对于给定的弹头，式（2）建立了起飞质量与主动段终点速度的关系.

假设助推系统的任务是将质量为907.8kg的滑翔弹头[6]助推至速度4 500m/s.根据式（2）可求得起飞质量m0＝18 013kg，进一步可计算出助推器装药质量为mp＝（m0－mf）（1－ε）＝15 394.7kg.通常导弹设计时需对主动段重推比（ν0＝m0g/（mpIp/t1））加以选择.参考一般固体火箭取值，重推比可取为ν0＝0.5，据此可求出助推器工作时间t1＝s，燃料质量流量平均推力Fp＝Ip＝353.08kN.

2 助推－滑翔导弹弹道优化模型

弹道优化设计的目的是获取一条或一类满足约束和性能指标条件的最优弹道.弹道优化问题可描述为一般的最优控制问题，即在时间区间[t0，tf]中，寻找最优控制变量u（t），最小化性能指标J，并使状态变量x（t）、初始时间t0、终端时间tf满足运动微分方程约束以及端点约束和过程约束.下面结合助推－滑翔导弹的特点，建立运动微分方程，确定约束条件及性能指标.

1）性能指标.

助推－滑翔导弹弹道复杂，宜分段进行弹道优化.滑翔弹头的主要优势即在于增大射程，总体设计时比较关心其射程覆盖范围，以Lf表示弹道终点处射程，可将滑翔弹头飞行段的性能指标取为J＝min（－Lf），即使射程最大.

主动段的主要作用是加速滑翔弹头，其射程在全弹道射程中所占比例很小，可将性能指标取为J＝－min[（gH＋v2/2）｜tf]，即主动段终点机械能最大，以利于滑翔弹头飞行段增大射程.

2）状态方程.

总体性能分析时主要关注导弹纵平面的运动，忽略地球自转和非球形影响，建立助推－滑翔导弹纵平面运动方程：

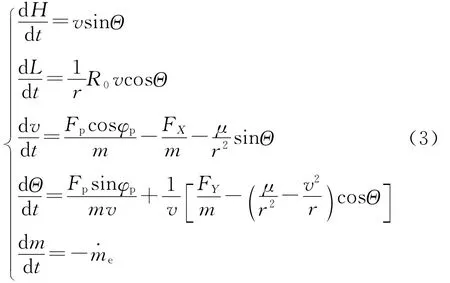
式中：H为飞行器距离地面的高度；L为射程；Θ为当地速度倾角；v为飞行器飞行速率；m为飞行器质量；e为发动机燃料质量流量；FX，FY分别为气动阻力、升力；r为飞行器到地心的距离；μ为地球引力系数；φp为推力与速度方向的夹角.

在优化问题中取状态变量x＝（HLvΘ m）T，主动段通过改变推力方向控制弹道，取控制量为φp；滑翔弹头段通过气动舵来改变弹道，而在仅考虑纵平面运动的情况下，飞行器动力取决于飞行器的速度、高度及攻角α，则取控制量为攻角α.

3）约束条件.

弹道设计时主要考虑飞行过程约束、终端参数约束及控制量约束.飞行过程约束，也就是飞行器在飞行过程中弹道参数必须满足的约束.为确保飞行器安全飞行，通常要考虑热流、法向过载、动压等因素对弹道的约束.具体有，法向过载约束：n＝，动压约束驻点热流约束＝ksρ0.5v3.15＜max.其中，ny，max，qmax，max分别为飞行中所允许的法向过载、动压和热流的最大值.

终端参数约束是指飞行器在弹道端点需满足的条件，即最优控制问题中的边界条件.主动段弹道起点参数取为导弹垂直上升段终点状态，滑翔弹头飞行段起点参数应当与主动段终点参数一致，滑翔弹头飞行段末端通常有落地速度与落地弹道倾角的要求，可取－Θ（tf）＝－60°，v（tf）＝1 000m/s.

另外，攻角、推力与速度方向的夹角等控制量的幅值和变化率不能超过限制值，可取｜α｜＜15°，｜φp｜＜5°，｜｜＜1 （°）/s，｜p｜＜1 （°）/s.

3 Gauss伪谱法优化基本原理

助推－滑翔导弹弹道形式复杂，飞行约束多，其弹道优化是一个难点.Gauss伪谱法（Gauss Pseudospectral Method，GPM）是一种适合解决多阶段多约束最优控制问题的数值优化方法，它将状态变量和控制变量在一系列Legendre Gauss（LG）点上离散，构造全局插值多项式来近似状态变量和控制变量，经过一系列处理，最终将最优控制问题转化为具有一系列代数约束的参数优化问题，即非线性规划问题（NLP），并进行数值求解.GPM离散最优控制问题的主要流程如下[7，8].

1）时域变换.

由于Gauss伪谱法的配点都分布在区间[－1，1]，因此求解中一般对时间区间进行变换，通过引入变换：

将最优控制问题的时间区间由t∈[t0，tf]转换至τ∈[－1，1]，并将原问题按时间归一化.

2）全局插值多项式近似状态与控制变量.

Gauss伪谱法的离散点κ＝｛τ1，…，τK｝为K阶Legendre－Gauss点，即K阶Legendre多项式的根PK（τ），其中，

Legendre－Gauss点分布在区间（－1，1），再增加一个点，τ0＝－1，作为区间[－1，1）上的K＋1个插值点，构成K＋1个Lagrange插值多项式li（τ）（i＝0，…，K），并以此为基函数近似状态变量和控制变量：

3）动力学方程约束转换为代数约束.

伪谱方法中，状态变量由全局插值多项式近似，状态变量的导数可通过求导来近似，从而将动力学微分方程约束转换为代数约束，即

式中，τk为LG点.微分矩阵D∈RK×（K＋1）可离线确定，将式（8）代入动力学方程：

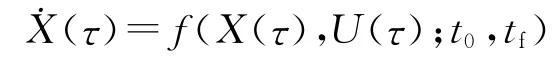
于是，将最优控制问题的动力学微分方程约束转换为代数约束：

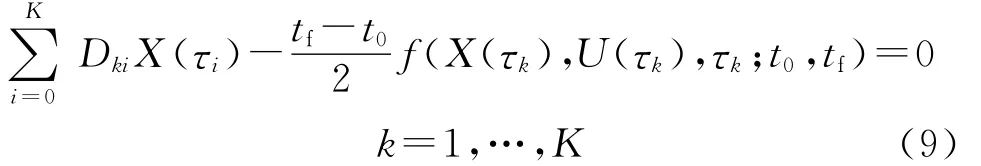
4）离散条件下的性能指标.

将Bolza型性能指标函数J＝Φ（X0，t0，Xf，tf）＋中的积分项用Gauss积分来近似，得到Gauss伪谱方法中的性能指标函数：

5）离散条件下的终端状态约束.

最优控制问题往往包含终端状态约束，根据动力学方程有：

将终端状态约束条件离散并用Gauss积分来近似，可得：

6）多阶段不连续问题的处理.

对于助推－滑翔导弹弹道优化这样的分段不连续最优控制问题，提出了多范围伪谱技术，即将问题分成若干子区间，在每个小区间上分别进行状态变量和控制变量的离散，在分段点处设置连接点，同时加上连接点约束条件.例如在某一点τ1∈[τ0，τ2]不连续，记

则连接点约束条件为

基于上述的数值近似方法，原连续最优控制问题被离散，并转换为非线性规划（NLP）问题.转换所得的NLP问题可采用数值方法求解，其中序列二次规划（SQP）是一种较好的选择，SQP算法较为成熟，在此不做介绍.BENSON和 HUNTINGTON等人的研究[9，10]证明了经GPM参数化得到的NLP问题的 KKT（Karush－Kuhn－Tucker）条件与离散的Hamiltonian边值问题（HBVP）最优性条件之间的等价性.除此之外，GPM的主要优点是算法以指数速率收敛，收敛速率快，且能在离散点较少时得到较好的精度.

4 优化算例

1）最大射程弹道优化.

助推－滑翔弹道的全弹道可划分为主动段和滑翔弹头飞行段，导弹经主动段弹道飞行，于关机点处滑翔弹头与助推级分离，分离后的弹头经自由飞行段飞行，再入大气层后依靠弹头的高升阻比气动性能进行滑翔机动飞行，最终以某落速和落角攻击目标.利用GPM对多阶段不连续问题的处理办法，主动段以关机点机械能最大为性能指标，以主动段关机点参数作为滑翔弹头飞行段起点参数，滑翔弹头段以射程最大为性能指标，分段进行弹道优化.

由于滑翔弹头飞行段射程占总射程的绝大部分，全弹道射程主要取决于主动段终点的运动参数及滑翔弹头的气动特性.在助推器与滑翔弹头参数确定的情况下，主动段终端参数由主动段控制规律决定.假设Hf，vf，Θf分别为主动段结束时刻的高度、速度和弹道倾角.经初步仿真发现，vf主要由助推器的总冲与推力程序决定，受主动段控制规律影响较小；Hf对总射程影响有限；Θf既对总射程影响大，又对主动段的控制较敏感，可取Θf为主动段弹道与滑翔弹头飞行弹道之间的衔接量.给定参数Θf的取值，性能指标与弹道约束不变，可得到不同Θf下的弹道曲线以及Θf与全弹道射程Lf的关系，如图1、图2所示.

图1 不同Θf对应的弹道曲线

图2 全弹道射程与Θf的关系

可见，Θf对弹道影响较大，且射程随Θf的变化趋势并不是简单的递增或递减.滑翔弹头飞行段弹道呈波状跳跃形式，当Θf小于18°时，全弹道曲线有4个波峰；当Θf在18°～25°之间时，弹道曲线有3个波峰；当Θf大于25°时，弹道曲线有2个波峰.波峰越多，射程越大.但在以上3种弹道形式中，分别存在3个射程的局部极大值，对应的主动段终端倾角为17°，23°，40°，其中Θf＝17°时全弹道射程最大，可将此最优倾角记为Θf，opt，其物理意义是保证在同样的主动段终点机械能条件下，最利于飞行器的能量利用，使射程达到最大值的最优倾角.

最大射程优化结果如图3～图6所示，可见主动段终点速度略大于4 500m/s，总射程3 300km，滑翔弹头飞行段射程占总射程的95.5%.落角、落速均严格满足端点约束，法向过载满足最大过载约束.最大射程弹道呈波状跳跃形式，大部分时间的飞行高度在30km以上，弹道较平滑.其中主动段结束至再入大气层（认为大气层边界高度为90km）之前的弹道，认为无控制作用，取控制量为零.

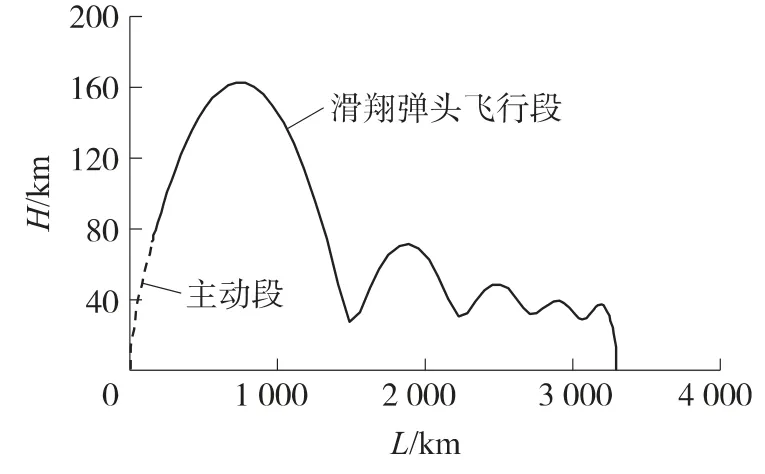
图3 弹道曲线

图4 速度曲线

图5 弹道倾角曲线

图6 控制量变化曲线

2）起飞质量与射程的关系.

无论是弹道导弹还是助推－滑翔导弹，其全弹道都可分为主动段和被动段，其中被动段又可分为自由飞行段、再入段两部分.对于弹道导弹而言，再入段射程在整个被动段射程所占比例很小，可近似将该段弹道看成是自由飞行段椭圆弹道的延续，从而整个被动段射程都用椭圆弹道来计算，其被动段最大射程以及对应的最优倾角可估算为

式中，vs为第一宇宙速度，R0为平均地球半径.结合式（2）、式（15）、式（16）即可得到弹道导弹起飞质量与最大射程的关系.

对于助推－滑翔导弹而言，再入段射程在整个被动段射程中占大部分，而再入段弹道形式复杂，射程很难用解析式表达.当起飞质量已知时，取助推火箭燃料比冲Ip＝2 800m/s，火箭结构比ε＝0.1，重推比ν0＝0.5，则可得到助推器基本参数.通过前面的方法，利用弹道优化技术，即得到此起飞质量下的最大射程与对应的主动段终端倾角.多次计算，即可得出起飞质量与最大射程的关系.计算结果如图7～图10所示.

图7 不同起飞质量下的高度－射程曲线

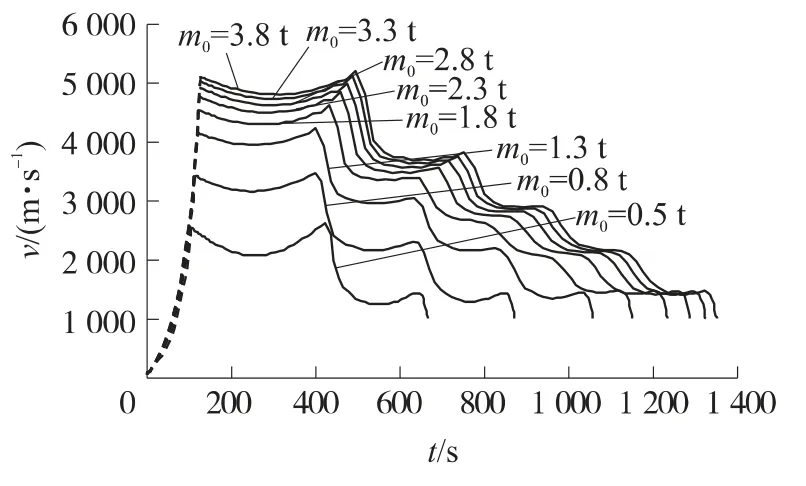
图8 不同起飞质量下的速度曲线

由图7、图8可见，起飞质量越大则主动段终点速度越大，全弹道射程也就越大.由图9可见，在达到同等射程的情况下，助推－滑翔导弹的起飞质量要远比弹道导弹小.由于采用单级火箭助推，在射程大于4 000km以上时，助推－滑翔导弹的起飞质量过大，此时宜采用多级火箭助推，以减小消极质量.由图10可见，与弹道导弹相比，助推－滑翔导弹最大射程对应的主动段终端倾角要小得多，这就要求导弹主动段具有较强的机动能力，以便完成转弯.

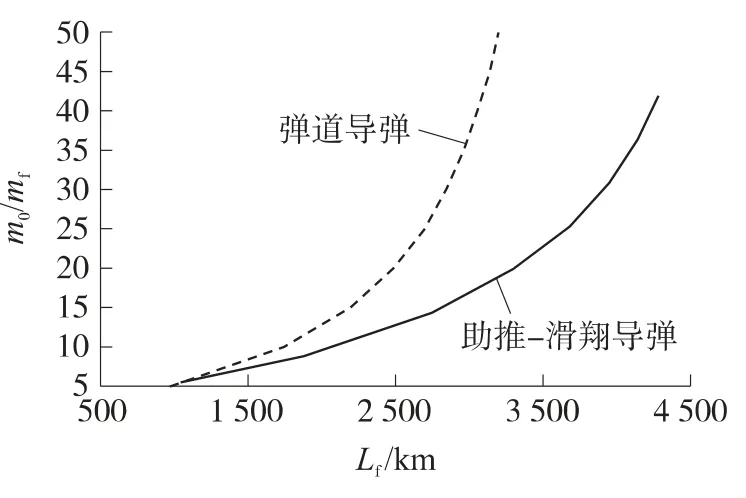
图9 质量比m0/mf随全弹道射程变化曲线

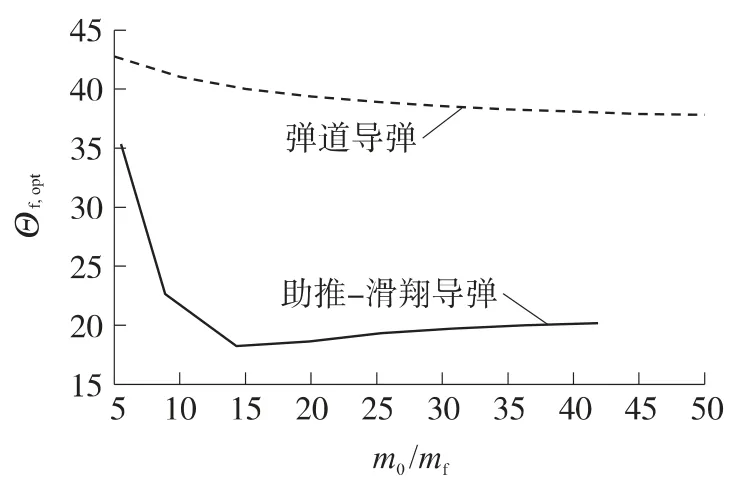
图10 最优倾角Θf，opt随m0/mf变化曲线

5 结论

本文推导了单级固体火箭助推飞行器起飞质量与主动段终点速度解析关系式，给出了助推器参数的估算方法.使用Gauss伪谱法对助推－滑翔导弹的全弹道进行了优化计算.采用分段优化的策略，以主动段终端倾角Θf为弹道衔接量，分析了Θf对射程的影响，结果表明存在使射程达到最大值的最优倾角Θf，opt，且此最优倾角与弹道导弹相应值相比要小得多.最大射程弹道的优化结果表明，Gauss伪谱法处理此类多阶段多约束的弹道优化问题效果较好，最优弹道起伏较小，攻角变化平滑，各项约束都得到满足.利用弹道优化计算，分析了助推－滑翔导弹起飞质量与射程的关系，并与弹道导弹进行了比较，结果表明助推－滑翔导弹在提高射程方面具有明显优势.

[1]刘欣，杨涛.滑翔导弹再入拉起段弹道优化设计与制导[J].国防科技大学学报，2012，34（1）：67－71.LIU Xin，YANG Tao.Trajectory optimization and guidance in reentry phase for glide missile[J].Journal of National University of Denfence Technology，2012，34（1）：67－71.（in Chinese）

[2]PERSTON H C，DARRY J P.Approximate performance of periodic hypersonic cruise trajectories for global reach[C].Proceedings of AIAA 8th International Space Planes and Hypersonics and Technologies Conference.Norfolk，VA：AIAA，1998：1－6.

[3]李瑜，杨志红，崔乃刚.助推－滑翔导弹弹道优化研究[J].宇航学报，2008，29（1）：66－71.LI Yu，YANG Zhi－hong，CUI Nai－gang.A study of optimal trajectory for boost－glide missle[J].Journal of Astronautics，2008，29（1）：66－71.（in Chinese）

[4]赵吉松，谷良贤，龚春林.高超声速飞行器起飞质量的解析估算[J].固体火箭技术，2008，31（6）：548－551.ZHAO Ji－song，GU Liang－xian，GONG Chun－lin.Analytical evaluation of takeoff mass for hypersonic vehicles[J].Journal of Solid Rocket Technology，2008，31（6）：548－551.（in Chinese）

[5]贾沛然，陈克俊，何力.远程火箭弹道学[M].长沙：国防科技大学出版社，1993：89－96，195－205.JIA Pei－ran，CHEN Ke－jun，HE Li.Ballistic for long－range rocket[M].Changsha：National University of Denfence Technology Press，1993：89－96，195－205.（in chinese）

[6]TIMOTHY R J.Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no－fly zone constraints[D].Ohio，USA：Air Force Insitute of Technology Graduate School of Engineering and Management，2007：88－89.

[7]雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D].长沙：国防科学技术大学，2008：49－53.YONG En－mi.Study on trajectory optimization and guidance approach for hypersonic glide－reentry[D].Changsha：National University of Defense Technology，2008：49－53.（in Chinese）

[8]杨希祥，张为华.基于Gauss伪谱法的固体运载火箭上升段轨迹快速优化研究[J].宇航学报，2011，32（1）：15－21.YANG Xi－xiang，ZHANG Wei－hua.Rapid optimization of ascent trajectory for solid launch vehicles based on Gauss pseudospectral method[J].Journal of Astronautics.2011，32（1）：15－21.（in Chinese）

[9]HUNTINGTON G T.Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[D].Massachusetts，USA：Massachusetts Institute of Technology，2007：51－57，115－143.

[10]BENSON D A，HUNTINGTON G T，THORVALDSEN T P.Direct trajectory optimization and costate estimation via an orthogonal collocation method[J].Journal of Guidance，Control，and Dynamics，2006，29（6）：1 435－1 440.