爆炸点火快速分离过程的理论与实验研究

姬 龙，黄正祥，顾晓辉，郑应民

（南京理工大学 智能弹药国防重点学科实验室，南京210094）

快速分离技术的研究一直以来受到人们的广泛关注，运用领域不断延伸，如带探测破－破式串联战斗部中前级战斗部的快速分离，破－穿式串联战斗部中随进战斗部的快速随进，舰艇巡航途中快速发射鱼雷、导弹对目标实施有效攻击等，都要求在最短的时间内将发射物体加速到最大速度，一定距离内缩短发射物体的反应时间.

传统的分离发射机制和作用原理中，火药装药点火方式主要采用电底火点火、点火头点火、等离子体点火、爆轰点火等，其中电底火点火和点火头点火技术已经相当成熟且应用广泛，但点火时间延时为几ms到十几ms，很难满足快速发射的要求[1]；李海元[2]和薛奡炜[3]等通过理论计算和实验研究，得出等离子体点火可以显著缩短火药的点火延迟时间，可控制在ms级以内，但其点火时需要特定装置，适用范围有限；张丁山[4]等采用爆轰点火方式可以实现点火延迟时间为0.3ms的目标，但其应用于引燃主装药，其后续的燃烧发射过程还需要一定延迟时间.目标机动性的不断加强对点火延迟时间提出更高要求.为了实现从点火到分离发射的延迟时间控制在ms量级以内，有必要在原有技术上进行深入研究.

本文设计了一种快速分离实验装置，采用爆炸点火方式，快速点燃发射药，靠发射药气体的推力剪断剪切环，实现前级分离体的快速发射.利用密闭爆发器原理和经典内弹道理论建立快速分离发射理论模型，并通过数值计算得到各物理参数的变化规律.

1 快速分离理论模型

快速分离发射主要是利用导爆索爆炸点火点燃发射药，使发射药迅速燃烧产生大量的高压气体，待药室内压力达到剪切环破坏极限时实现前级分离体的快速分离发射.模拟装置如图1所示.

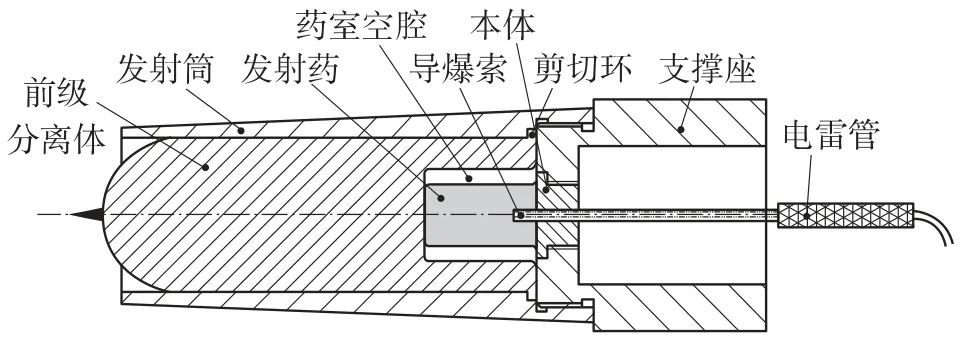
图1 快速分离装置示意图

通过上述分析将分离过程分为2个阶段：第一阶段为发射药开始燃烧到发射药气体压力达到剪切环破坏极限，即快速燃烧阶段；第二阶段为剪切环被剪断至前级分离体增速到最大速度，即快速发射阶段.在此过程中，假设：剪切环瞬间剪断，即达到剪切环破坏极限后，前级分离体开始运动.

1.1 快速燃烧阶段

此阶段中，药室空腔体积没有发生变化，并且发射药气体也没有对外做功，所以可近似看作密闭爆发器，运用其原理对此过程进行分析.

将几何燃烧定律条件下定容燃烧的p-t理论曲线和密闭爆发器实测p－t曲线进行对比，从而得到理论p－t曲线的斜率dp/dt的表达式，即p－t曲线应满足的微分方程[5]：

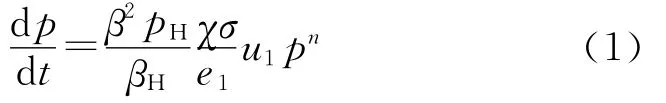
式中，pB为点火压力；f为火药力；ω为发射药质量；ψ为火药已燃百分数；S为药室横截面积；lψ为药室自由容积长；pH为初始剪切压力；βH为达到pH时对应的β值；σ为火药相对燃烧面积；e1为1/2火药起始厚度；u1为燃速系数；χ、μ和λ为火药形状特征量；n为燃速指数；Z为火药已燃相对厚度；α为发射药燃气余容；ρp为发射药密度；Fτmax为剪断剪切环所需的最大剪切力.

通过选取合适的pB和u1可以较好地反映爆炸点火时发射药燃烧规律，并将式（2）～式（5）代入方程（1）进行求解，可得第一阶段各参量的数值.

1.2 快速发射阶段

当发射药气体压力达到剪切环破坏极限时，剪切环发生瞬间剪切，前级分离体开始加速运动，在上阶段条件基础上建立动态下内弹道方程组[5～7]：

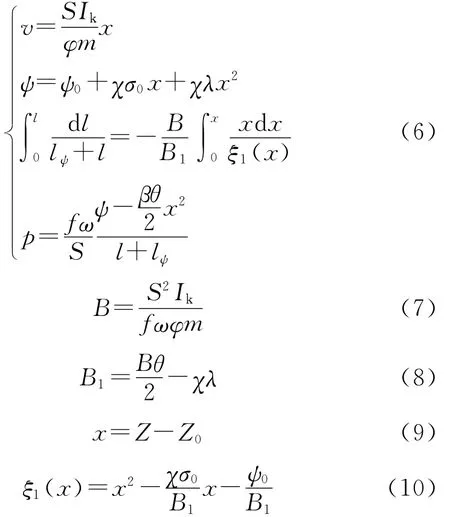
式中，Ik为压力全冲量；φ为次要功计算系数；m为前级分离体质量；θ＝k－1，k为绝热指数；Z0、ψ0、σ0为达到剪切环破坏极限时各参数的取值.

由此解出发射过程中前级分离体速度v、行程l、膛内压力p之间的关系.

1.3 数值求解

运用上述建立的快速分离发射内弹道理论模型，忽略前级分离体剪切过程对内弹道性能的影响，选取双基圆片状发射药，e1＝0.07 mm，f＝1 180kJ/kg，ω＝3g，ρp＝1 650kg/m3，分离体的质量m＝260g，材料为超硬铝（7A04），且Fτmax＝125 MPa.利用Matlab中四阶Runge－Kutta法编程计算，结果如图2～图4所示.

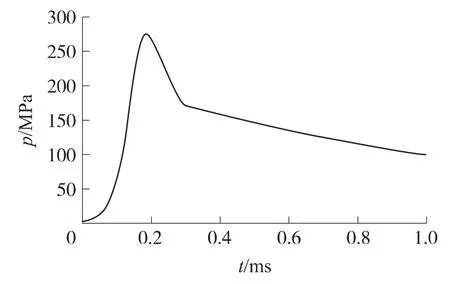
图2 快速分离发射时期膛内p－t曲线

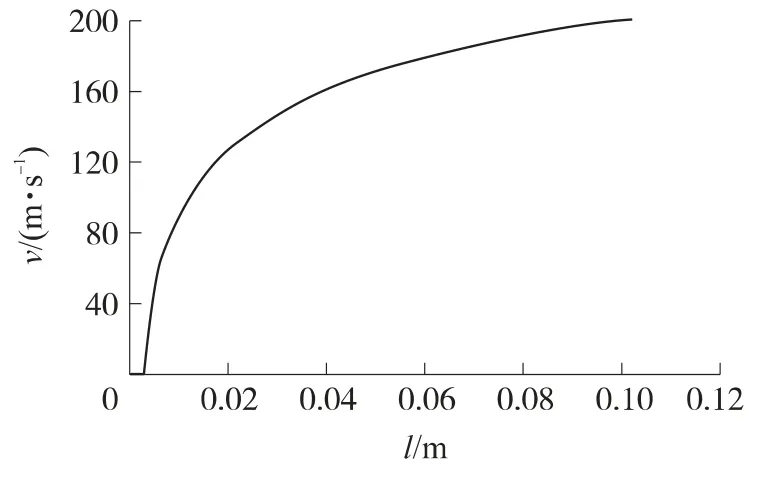
图3 前级分离体在膛内的v－l关系曲线

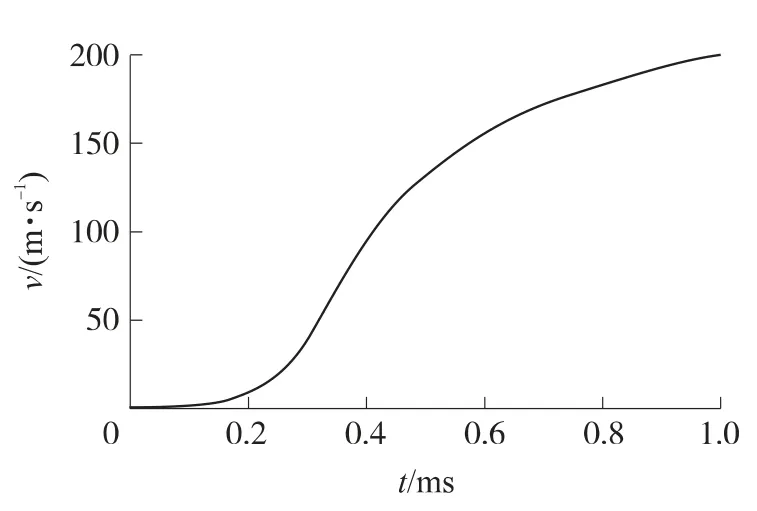
图4 前级分离体在膛内的v－t关系曲线

从图2～图4得出快速分离发射内弹道时期膛压、前级分离体速度以及膛内运动的规律.由图2可得，膛内压力达到剪切环剪切压力所用时间约为125μs.由图3可得，前级分离体发射时的位移与速度关系，前级分离体分离速度为200m/s.图4表明前级分离体在125μs时开始运动，到1 ms时前级分离体速度达到最大值200m/s.

2 快速分离实验研究

根据理论计算结果，本文通过静态台架实验对其进行验证，模拟爆炸点火方式下前级分离体快速分离发射过程，通过测试仪对分离时间和分离速度进行测试，利用高速摄像进行验证.

2.1 实验原理

实验采用电雷管引爆Φ2.88mm铅制导爆索，通过导爆索爆炸点燃双基片状发射药，待发射药气体压力达到剪切环剪断压力时，前级分离体开始增速运动.为了精确测试快速分离时间，现选用光电耦合器，实现电雷管起爆与测试仪信号输入同步，见图5.

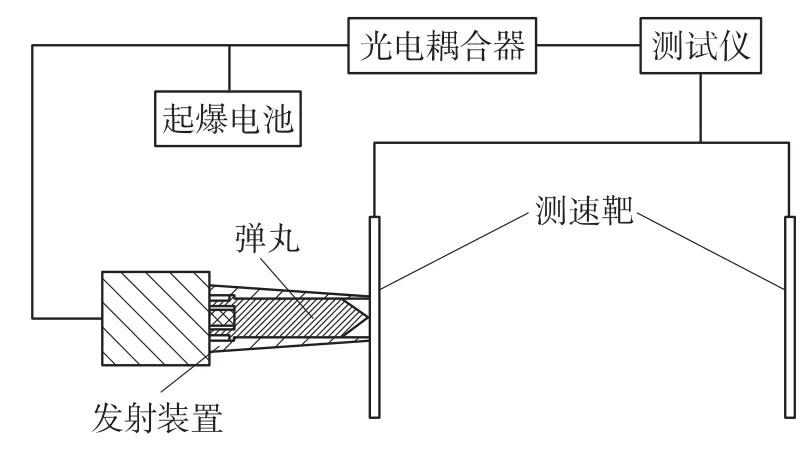
图5 模拟实验装置布局示意图

2.2 实验结果及分析

通过上述实验，对快速分离发射装置的分离时间和分离速度进行测试，实验结果见表1.

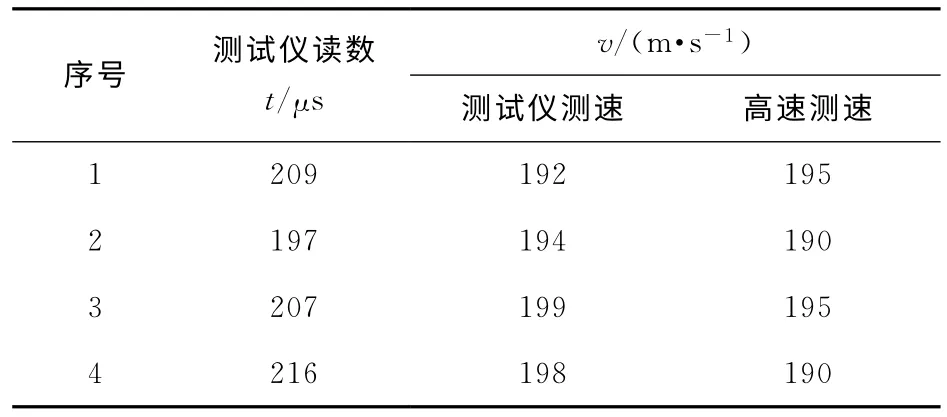
表1 分离时间与分离速度实验结果表

从表1可得，通过瞬态测试仪测试快速分离时间为197～216μs，发射速度为192～199m/s；由高速摄像测得前级分离体的发射速度为190～195m/s.与图2～图4中数值解进行比较，其分离时间为125μs，两者差异较大.这主要是由于瞬态测试仪测得的分离时间为：从雷管接收到点火信号到发射药气体压力达到剪切环剪切压力时所用时间，包括雷管延时和导爆索传爆时间，所以测试时间偏长.通过计算，导爆索传爆时间tA＝16μs，电雷管延时时间tB＝50μs.由此可得测试分离时间为131～150μs，与计算结果相比偏差为4%～13%.测试结果中发现测试时间有波动，这主要是由测试手段、测试仪响应快慢、干扰等多方面因素引起的，发射时间极短，测试灵敏度要求高，易受干扰.这种误差范围内的波动是允许的.

由此可见，采用快速分离发射装置，利用爆炸点火点燃发射药的方式，可以有效提高分离时间.这主要是由于传统分离发射装置中，热传导方式在点火能量传播过程中占主要地位，不能使发射药完全同时点燃，只能点燃一部分逐层传递，发射药气体的生成速率不高，导致气体压力剪断剪切环时间增长；而爆炸点火方式是利用雷管引爆导爆索，由导爆索爆炸产生爆轰能量点燃发射药，甚至部分发射药发生爆燃，穿透和侵蚀作用较为显著，发射药几乎同时燃烧，并且导爆索附近的发射药在其爆炸作用下碎裂，起始燃面增加，燃速增大，点燃较为容易，从而发射药气体的生产速率陡升，在较短的时间内气体压力超过剪切环最大抗剪切力，实现快速分离.

同时，在前级分离体剪断剪切环时，发射药气体压力较大，前级分离体获得较大初始加速度，在较短的发射筒行程内，快速增速，在分离时，达到预期发射速度.由图3、图4得数值解中发射速度v＝200m/s，与测试结果基本吻合.由此可证明，快速分离发射理论模型是正确的，为快速分离优化设计提供了理论支持.

3 结论

①快速分离发射装置在一定条件下，可实现分离时间在200μs左右，发射速度为200m/s，满足分离战斗部技术要求.

②利用密闭爆发器原理和发射时期内弹道理论，对分离时间和分离速度进行数值计算，计算结果与实验结果吻合较好，与实际接近，可近似反映出特定实验装置内，爆炸点火方式下内弹道变化诸元.为今后工程优化设计提供理论支持.

③本实验装置利用爆炸点火方式点燃发射药，可以大幅度提高前级分离体的分离时间与发射速度，为实现快速分离发射研究提供依据.

[1]张丁山.爆轰快速点火实验研究及机理分析[J].爆炸与冲击，2011，31（2）：185－190.ZHANG Ding－shan.Experimental investigation and mechanism analysis on high－speed ignition by detonation [J].Explosion and Shock Waves，2011，31（2）：185－190.（in Chinese）

[2]李海元.等离子体点火密闭爆发器中火药燃速特性的研究[J].爆炸与冲击，2004，24（2）：145－150.LI Hai－yuan.Propellant burn rate characteristics in closed bomb ignited with plasma[J].Explosion and Shock Waves，2004，24（2）：145－150.（in Chinese）

[3]薛奡炜.发射药等离子体点火与常规点火性能的比较[J].弹道学报，2009，21（3）：61－64.XUE Ao－wei.Comparison of plasma and conventional ignition performance of propellants [J].Journal of Ballistics，2009，21（3）：61－64.（in Chinese）

[4]张丁山.爆轰快速点火过程的数值仿真与实验研究[J].兵工学报，2010，31（4）：423－428.ZHANG Ding－shan.Numerical simulation and experimental study of high speed ignition by detonation[J].Acta Armamentarii，2010，31（4）：423－428.（in Chinese）

[5]金志明.枪炮内弹道学[M].北京：北京理工大学出版社，2004：9－117.JIN Zhi－ming.Gun interior ballistics[M].Beijing：Beijing Institute of Technology Press，2004：9－117.（in Chinese）

[6]丘尔巴诺夫E B.挤进时期内弹道学与挤进压力计算[M].杨敬荣，译.北京：国防工业出版社，1997.

[7]翁春生.计算内弹道学[M].北京：国防工业出版社，2006.WENG Chun－sheng.Computational interior ballistics [M].Beijing：National Defense Industry Press，2006.（in Chinese）