防空火箭炮刚柔耦合发射动力学仿真
2012-12-25马大为周克栋于存贵
王 雷,马大为,周克栋,于存贵
(南京理工大学 机械工程学院,南京210094)
防空火箭炮的物理结构与用于火力支援的普通火箭炮完全不同,为了增加毁歼目标的概率,要求多枚弹同时点火发射,以适应对空中移动目标进行拦截的要求[1],因此建立更精确的刚柔耦合动力学仿真模型对火箭炮进行优化设计、性能测试和制造仿真显得尤为重要.现今火箭炮刚柔耦合动力学模型对柔体处理一般采用模态缩减法的第二代多柔体技术[2],该方法是将柔性体结构的刚度通过有限元计算获得的模态来表示,将多体动力学和有限元相结合,有效地解决了诸多领域的工程问题,而且有较高的计算效率,但无法处理柔性体边界条件的改变,也无法处理柔性体材料的非线性.最新多柔体处理技术采用有限元“节点法”将有限元和多体系统放在同一求解器中求解,可以弥补上述不足,考虑了柔性体结构间的碰撞和接触以及考虑了非线性变形,但有限元法计算量大,求解效率低.综合考虑2种柔性处理方法的优缺点,本文同时采用2种柔性体处理方法建立防空火箭炮刚柔耦合动力学模型,既可以提高计算精度又可以保证计算效率.
1 基本理论研究
研究多柔体动力学问题,需要将多刚体系统动力学理论和柔性多体动力学基本理论相结合.本文将着重研究基于有限元节点相对坐标法的多柔体理论,在建立动力学方程时采用相对节点位移法,通过叠加沿通路所有节点的相对变形量获得节点的绝对变形量.设节点i-1为节点i的内节点,节点i在惯性坐标系下的位置和姿态通过节点i-1的相应量和相对节点位移表示为
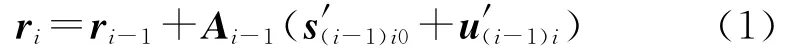
式中,Ai-1为节点i-1参考系的转换矩阵,s′(i-1)i0为未变形状态下节点i在节点i-1参考系下的位置矢量,设节点的相对位置和方向位移的广义坐标为u′(i-1)i和Θ′(i-1)i,则:
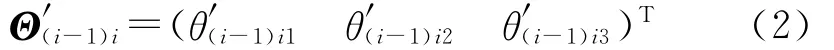
式中,θ′为节点相对角位移的坐标分量,将式(1)变形后得到:
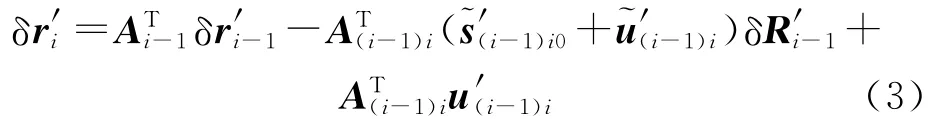
式中,带“~”的变量表示由矢量元素组成的斜对称阵.定义A(i-1)i=ATi-1Ai,节点i和i-1之间的虚转动关系为
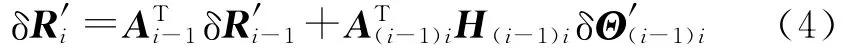
式中,
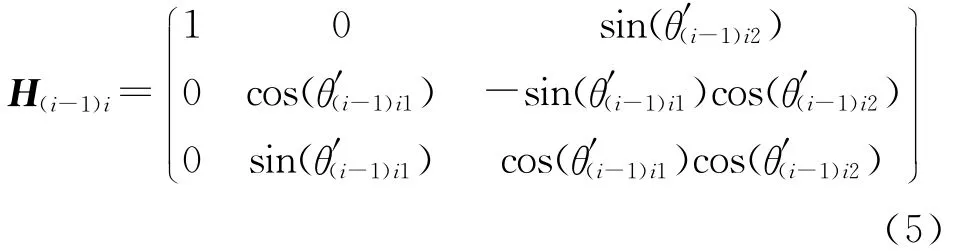
联立式(3)和式(4)得到相邻两节点之间的虚位移关系方程:
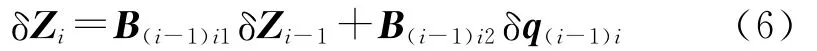
式中,
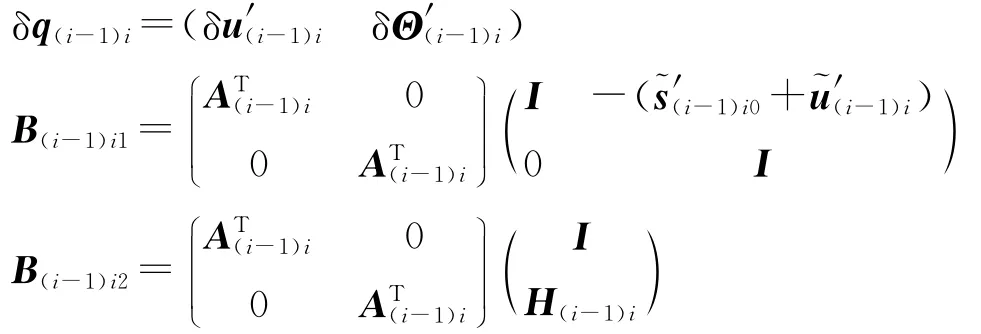
沿通路多次应用式(6)可得整个柔性体的笛卡尔坐标和相对坐标虚位移关系为

多节点有限元单元的应变能只受单元内节点坐标系的相对位移的影响,与刚体运动无关,所以系统应变能变化可表示为
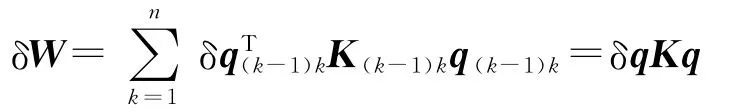
式中,K为单元刚度矩阵.由绝对坐标系的节点力F1和相对节点坐标系的节点力F2所做虚功为
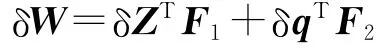
将式(7)代入上式,得:

式中,F*1=BTF1+F2.对于约束系统,Φ和λ分别表示约束方程和相应的拉格朗日乘子,应用拉格朗日乘子定理获得以下柔性平衡方程为[3,4]

基于相对坐标法推导的多刚体动力学平衡方程[5]为
式中,ΦZ为多刚体系统所有铰在笛卡尔坐标系下的约束关系,M为系统质量矩阵,为系统加速度矩阵.
式(8)和式(9)结构近似,用同一积分器求解就能实现刚体和柔性体的精确耦合计算,耦合计算只需在多体系统中通过有限元的网格和材料等信息表示柔性体.
2 刚柔耦合多体动力学建模
该型火箭炮的实体结构比较复杂,应用多体动力学的观点,抽象出体现系统特性的因素,将研究的防空火箭炮系统简化为由车体、底座、回转体、起落架、2个储运发射箱、40根定向管、40枚火箭弹等刚体部分组成,并赋予各部件等效实际结构的质量、质心位置和转动惯量等参数[5].在精确的多刚体模型基础上,采用“模态缩减”法和有限元“节点法”生成柔性体替换刚性体,建立刚柔耦合模型.本文利用RecurDyn软件对整炮进行刚柔耦合建模,其模型如图1所示.

图1 防空火箭炮刚柔耦合模型
2.1 车体的建模
如图2,发射车前后用4个千斤顶支撑于地面,千斤顶与地面的连接采用轴套力模拟,轴套力分别有3个移动自由度和转动自由度,每个自由度都有刚度系数和阻尼系数,正好可以模拟汽车绕地面的平移和转动,通过动静平衡可确定轴套力预载,以平衡系统重力.千斤顶为液压千斤顶,在不考虑渗漏条件下,可以用具有同样刚度的等效弹簧来代替千斤顶在液压压力作用下发生的可压缩流动.千斤顶与车体刚性大梁之间采用固定铰连接,车身与刚性大梁之间采用固定铰连接.
在ANSYS软件中建立车大梁模型,为了避免刚体与柔性体连接产生的应力集中现象,需在有限元模型中把与刚体连接的部分和刚性连接点建立多点耦合约束关系,这样就可以把刚性连接点上的力均匀传递到连接面上[6].对大梁有限元模型进行模态分析生成柔性大梁,并导入RecurDyn软件中,替换刚体大梁,柔性大梁与车轴、车身和千斤顶的连接采用固定副,连接点必须是有限元模型中定义的刚性连接点,柔性大梁与各构件的连接关系如图2.
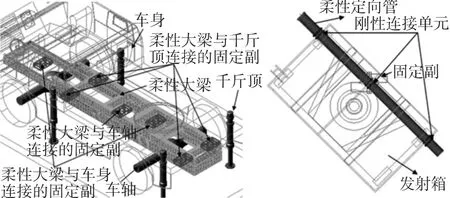
图2 柔性大梁、定向管与刚性构件的连接关系
2.2 整炮的建模
火箭炮底座用固定铰固连在车身上.起落架与回转体之间的关系可以描述为俯仰轴与起落架固定,俯仰轴与减速器之间采用旋转副连接,减速器与回转体之间采用固定铰连接,采用模态缩减法生成柔性俯仰轴替换刚性轴,柔性轴模型如图3所示,减速器的刚度由等效扭簧来模拟,扭簧的刚度和阻尼由减速器型号参数确定.回转体与底座之间的动力学关系采用相同的建模方法实现.刚性定向管与发射箱之间、发射箱与起落架之间均采用固定铰连接.
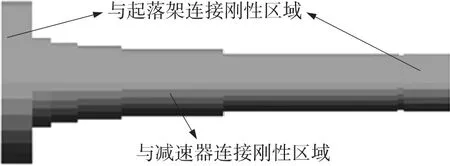
图3 柔性俯仰轴
建立定向管几何模型,在有限元软件中划分网格,处理并生成含有单元属性和材料特性信息的.cdb文件[7].将定向管的有限元模型导入RecurDyn软件中,替换刚性定向管,在柔性定向管中心轴线上创建主节点,定义定向管与发射箱连接区域的节点为从节点,生成主节点与从节点耦合的刚性连接单元,柔性定向管通过主节点与刚性发射箱采用固定副连接,如图2所示.
2.3 载荷的施加
防空火箭系统发射过程受到的力有重力、各部件之间以及火箭炮与地面之间的机械作用力、弹管作用力、发动机推力、燃气流冲击力等.其中,火箭炮各部件之间的作用力、火箭炮与地面之间的作用力均可等价为弹性铰对应的作用力和相应的阻尼力,它们都是系统内力.
火箭弹推力曲线数据由实验测得,按照Akima函数二次曲线拟合方法得到样条曲线,并通过集中力作用于火箭弹的尾部.
考虑燃气流场对火箭炮结构的影响,在制定多枚弹同时发射的火箭弹管位时,要保证每2枚弹间的最远安全距离,燃气射流冲击力由气体动力学软件仿真计算获得,用Akima方法拟合为随距离变化的集中力,施加在定向管轴线与定向管口平面的交点上.
火箭弹所受闭锁力为1 800N,采用轴套力模拟,当火箭弹的推力达到闭锁力大小后轴套力连接失效,弹解锁运动.
发射时,火箭弹定心部和定向钮通过与定向管内壁和螺旋导槽接触碰撞使其前进,刚性火箭弹与柔性定向管之间建立面面柔性接触关系,“节点法”柔性建模时可以处理边界条件的改变,弹管间柔性接触是典型变边界条件问题,通过将管内壁柔性面作为作用面,弹定心部刚性表面作为基面,基面划分为三角形碎片,作用面依据有限元单元类型划分为多个三角形或四边形碎片.在计算时,程序先检查作用面的单元节点是否与基面上的碎片接触,若接触,则其接触力计算公式为
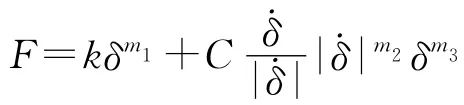
式中,k为接触刚度系数,C为阻尼系数;m1、m2、m3分别为刚度指数、阻尼指数以及凹痕指数(当渗透深度很小的时候,接触力会出现负值,可通过采用大于1的凹痕指数避免),δ为穿透深度.
3 刚柔耦合动力学仿真及结果分析
车载防空火箭炮采用4枚或2枚同时点火的发射方式,即首先齐射4枚弹,隔一个时间间隔齐射4枚,再隔一个时间间隔齐射2枚,然后重复.考虑到刚柔耦合模型的复杂程度及有限元单元数不能太多,本文只对一组4枚弹同步发射的工况进行刚柔耦合发射动力学仿真(即4个发射定向管被柔性化),射角如图1所示,俯仰角为45°,方位角为90°.
仿真结果后定心部出管口时间t2以及出管口时火箭弹速度v2与实验测得对应数据的比较,如表1所示,表中,t1和v1分别为中定心部离管时间与离管速度.计算获得的柔性定向管自然频率fn与实验结果,如表2所示.仿真结果与测试结果非常接近,考虑到模型简化带来的误差、实验测试误差和实验环境的差异,可认为采用上述的刚柔耦合模型、方法和参数是可行的,仿真结果是准确、可信的.

表1 仿真结果与测试数据比较
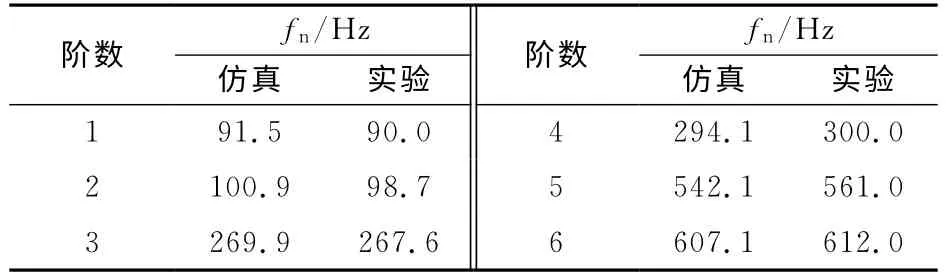
表2 柔性定向管计算自然频率与实验数据比较
图4~图7为发射过程中定向器管口俯仰和方位运动曲线,图8和图9分别为火箭弹后定心部与定向管内壁、定向钮与螺旋导槽的碰撞接触力曲线,图中实线为刚柔耦合模型的仿真结果,虚线表示对应多刚体模型的仿真结果.
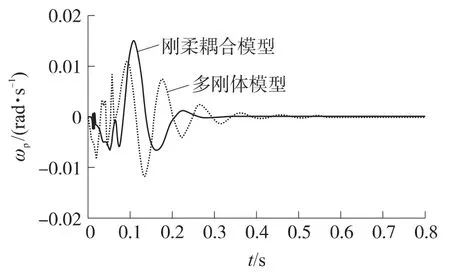
图4 定向器管口俯仰方向角速度
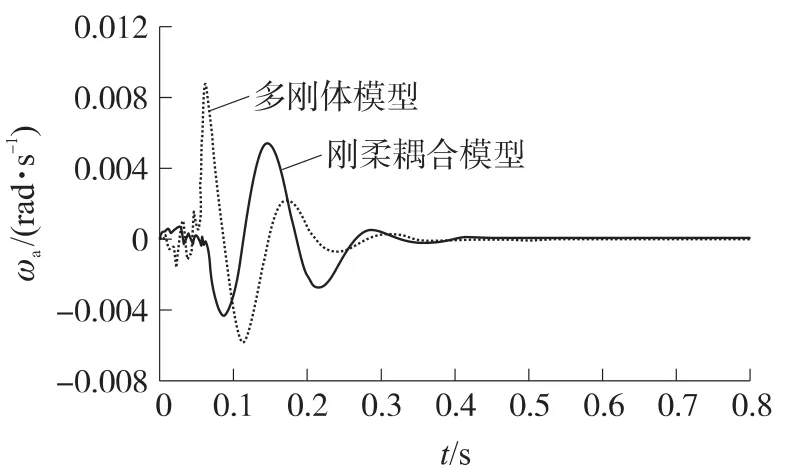
图5 定向器管口方位方向角速度
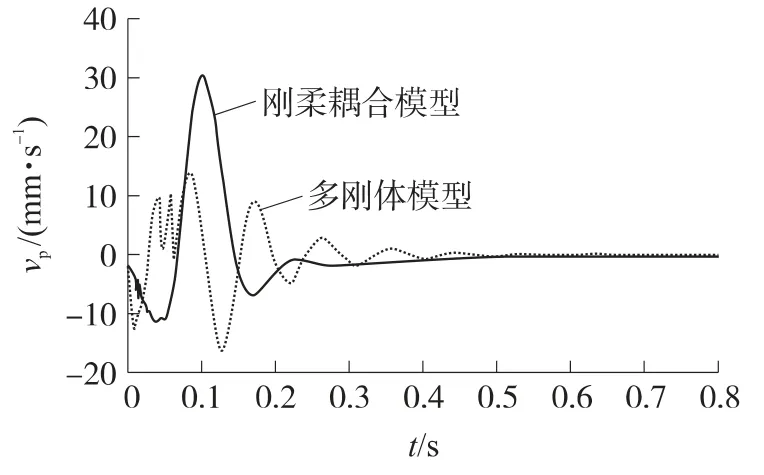
图6 定向器管口俯仰方向线速度
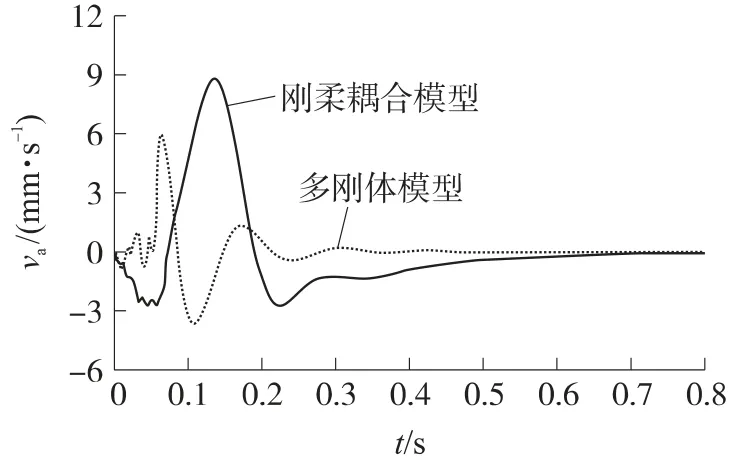
图7 定向器管口方位方向线速度
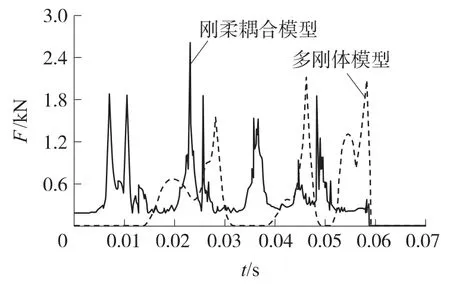
图8 后定心部与管内壁接触力曲线

图9 定向钮与螺旋导槽接触力曲线
对比刚柔耦合模型与多刚体模型的仿真结果,可以看出:在火箭弹点火到尾部离管的0.06s时间内,由于定向管柔性阻尼的作用,火箭弹在柔性管内运动产生的管口扰动连续蠕动变化、相对平滑、不存在较大突变,曲线的第一个峰值出现较晚,而多刚体模型的第一个曲线峰值出现较早;在0.06s瞬间,由于燃气射流冲击力的作用,柔性管口角速度产生剧烈颤动,如图4和图5所示;刚柔耦合模型的俯仰角速度、方位角速度曲线具有较快的衰减速度;多刚体模型将定向管视为刚体,从而将其归并到俯仰部分中,彻底忽略其柔性效应.从多刚体仿真结果也可以看出,俯仰和方位角速度与线速度近似成线性比例关系,而由于定向管和车大梁的弹性变形的影响,线速度与角速度并不是简单的线性关系,刚柔耦合结果更符合实际情况.相比于刚体与刚体接触,刚柔接触作用力曲线变化规律更复杂,而且在波动过程中连续不断颤动,与实际情况相比具有更好的相似性.
4 结论
刚柔耦合动力学模型相对多刚体模型建模要复杂,由于柔性体阻尼效应的作用,火箭炮管口的动力学曲线相对平滑,衰减更快;车大梁和定向管的弹性变形使管口的扰动幅值增加;刚柔耦合模型结果更准确地反映了火箭炮系统在发射过程中的动力学特性;为获得较真实的系统动态特性,对细长、刚性差以及有较大变形的部件,在动力学仿真建模时应作柔性处理.本文重点研究了防空火箭炮系统的刚柔耦合动力学建模方法,为今后进一步研究改善射击密集度等性能参数奠定了基础.
[1]陈兵,马大为,乐贵高,等.群射防空火箭炮射序优化[J].弹道学报,2006,18(4):25-28.CHEN Bing,MA Da-wei,LE Gui-gao,et al.Firing orders optimization of aero-defence rocket launcher by volley firing[J].Journal of Ballistics,2006,18(4):25-28.(in Chinese)
[2]冯勇,马大为,薛畅,等.多管火箭炮刚柔耦合多体发射动力学仿真研究[J].兵工学报,2006,27(3):545-548.FENG Yong,MA Da-wei,XUE Chang,et al.Simulation studies of coupled rigid and flexible multi-body dynamics for multiple launch rocket systems[J].Acta Armamentarii,2006,27(3):545-548.(in Chinese)
[3]YOO H,RYAN R,SCOTT R.Dynamics of flexible beams undergoing overall motion[J].J Sound and Vibration,1995,181(2):261-278.
[4]BAE D S,HAUG E J.A recursive formulation for constrained mechanical system dynamics:PartⅡclosed loop systems[J].Mech Struct and Machines,1995,181(2):261-278.
[5]宫鹏涵,陈锦喜,李永建,等.某榴弹发射器刚柔耦合动力学建模与仿真研究[J].兵工自动化,2008,27(2):46-48.GONG Peng-han,CHEN Jin-xi,LI Yong-jian,et al.Modeling and simulation for the rigid-flexible coupling dynamics of the automatic grenade launcher[J].Ordnance Industry Automation,2008,27(2):46-48.(in Chinese)
[6]傅德彬,姜毅,刘琦.发射装置刚柔耦合仿真分析[J].弹箭与制导学报,2004,24(5):425-428.FU De-bin,JIANG Yi,LIU Qi.Rigid-flexible coupled simulation of guided missile launcher[J].Journal of Projectiles,Rockets,Missiles and Guidance,2004,24(5):425-428.(in Chinese)
[7]于存贵,申亮,马大为.舰炮刚柔耦合发射动力学仿真[J].系统仿真学报,2009,21(23):7 694-7 696.YU Cun-gui,SHEN Liang,MA Da-wei.Study on simulation for rigid-flexible coupling launch dynamics of naval gun[J].Journal of System Simulation,2009,21(23):7 694-7 696.(in Chinese)
