考虑动态接触参数的某型导弹发射动力学分析
2012-12-25刘馨心徐宏斌张亮亮褚福磊
刘馨心,徐宏斌,张亮亮,褚福磊
(1.清华大学 精密仪器与机械学系,北京100084;2.西安现代控制技术研究所,西安710065)
初始扰动是各类武器研制需要解决的一个重要问题.对导弹系统来说,过大的初始扰动会加重制导系统负担,甚至造成导弹失控.目前对初始扰动的研究主要考虑了推力偏心、质量偏心、动不平衡[1]等因素,而考虑结构间隙带来的系统动特性影响的分析不多见.
由于设计需要或加工误差等原因,导弹发射系统不可避免地存在运动副间隙,导弹在发射出筒过程中的动力学特性会受到间隙的影响,从而影响导弹的初始扰动.因此,在导弹发射系统建模过程中考虑运动副间隙影响,引入接触碰撞模型,将有助于更加真实、准确地研究系统参数对导弹初始扰动的影响,为导弹发射系统的设计以及提高发射精度提供参考.
研究系统间隙碰撞问题的关键是要解决接触碰撞阶段的动力学模型,而模型的难点在于接触参数的确定[2~5].本文以某单位研制的反坦克导弹武器系统为研究对象,基于接触变形碰撞模型,考虑接触刚度、阻尼系数和穿透量的动态变化,利用动力学软件建立了研究对象的动力学模型,通过数值仿真计算得到了系统的动力学响应.
1 接触碰撞模型的建立
1.1 碰撞接触力模型
经典碰撞模型认为碰撞在瞬间完成,忽略了接触过程,因此无法给出碰撞发生时的接触力变化和碰撞时间等信息,但是系统的运动参数动态响应是需要关注的重要特性,因此,采用等效的接触变形碰撞模型来描述系统各部件之间的接触较为合适.
DUBOWSKY[2]提出即使在较小的碰撞速度下,碰撞点邻域内仍会存在微小变形,并由弹簧阻尼系统来等效碰撞力的大小,其广义形式可表示为

式中,Fn为接触点处法向接触力,Kn为等效接触刚度,C(δ)是与δ有关的阻尼因子,δ和为接触点法向穿透深度及法向相对速度,非线性指数因子m≥1.不同的m、Kn和C(δ)代表不同的模型,常见的有基于Herts理论的接触模型、基于DUBOWSKY线性化处理的碰撞模型以及非线性等效弹簧阻尼模型等,但这几种模型里的接触参数均是与系统运动特性无关的量.
HUNTER[3]分析了2个弹性球的碰撞运动过程,如图1所示,质量m2的小球以速度v0撞向质量m1的小球,推导得撞击过程中的最大撞击力为
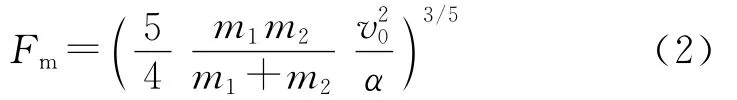
最大挤压量为

式中,

式中,E、ν、R分别为小球的杨氏模量、泊松比和曲率半径.
对于圆柱与圆筒碰撞,此时的α为

由式(2)、式(3)可看出,Fm和δm均是与物体相对碰撞速度有关的量.文献[4]通过对转子和定子碰撞过程的线性化处理,并对比文献[3]的计算结果,得到了两刚体碰撞的线性当量化接触刚度计算公式.徐振钦等人[5]将这种碰撞模型引入到火箭武器发射过程中的弹管接触碰撞多体系统动力学模型中,得到了较好的计算结果.

图1 两弹性球相撞
本文采用线性当量化的方法,用等效弹簧-阻尼模型来模拟局部撞击处的弹性挤压这一非线性过程,其中弹簧刚度为K,阻尼系数为c,线性当量化的弹簧-阻尼模型如图2所示.

图2 线性当量化的弹簧-阻尼模型
当弹簧-阻尼系统处于接触状态时,系统的运动微分方程为
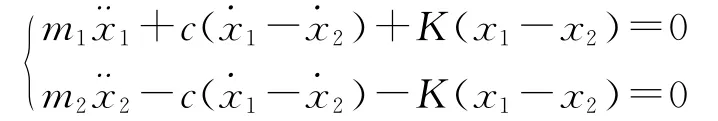
初始条件x1(0)=0,x2(0)=0,1(0)=0,2(0)=v0,通过正则化方法计算得到2个小球的位移响应为
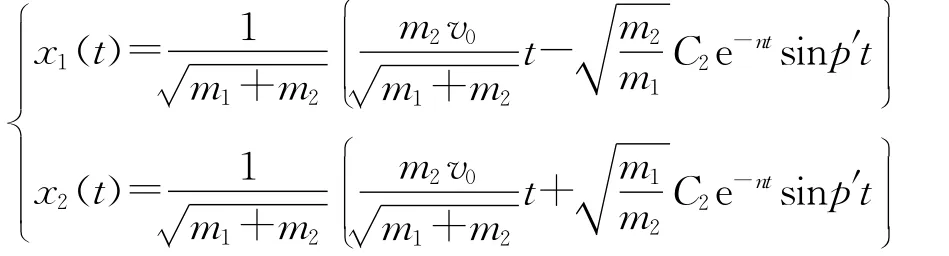
速度响应为
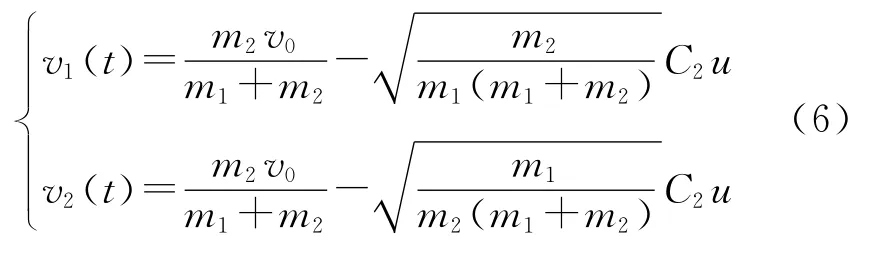
式中,
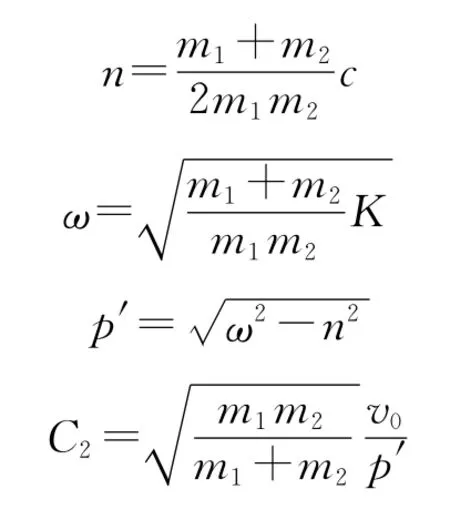

则两小球在相撞过程中的相对距离为
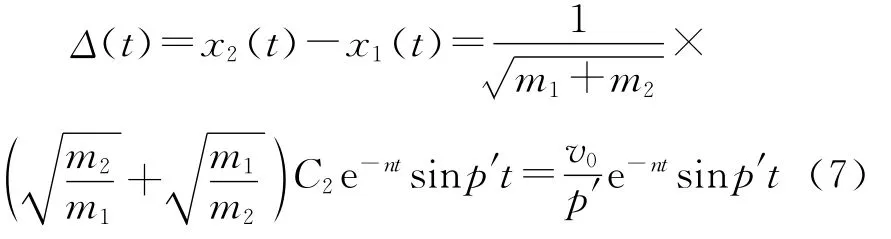
设tm为碰撞过程达到最大挤压量的时刻,此时(tm)=0,弹簧阻尼系统产生的作用力由弹簧提供,则:

将式(2)和式(3)代入式(8),得线性当量化的刚度系数K为

阻尼系数的存在导致碰撞前后的能量损失.设时刻ts为两小球碰撞结束时刻,则有:

取该分析模型具有物理意义的时刻,得到:

将式(11)代入式(6),得到两小球碰撞结束时的能量为

用恢复系数法求得两小球碰撞结束时的能量为

式中,e为恢复系数.
2种计算方法求得的能量值相等,将式(12)和式(13)对比化解即可得到线性当量化后的阻尼系数为

这与文献[6]得到的结果一致.
将式(9)和式(14)代入式(1),取m=1便可得到用等效线性当量化的弹簧-阻尼模型处理的接触点处的法向接触力.
从式(3)、式(9)和式(14)可以看出,该接触碰撞模型的等效接触刚度、阻尼系数和穿透深度除了与接触处的材料参数有关外,还与相对碰撞速度有关,它们在运动仿真过程中是变量.
1.2 摩擦力模型
接触点的切向相对运动分为相对滑移和粘滞2种情况.接触滑移状态时可认为其摩擦力作用符合库伦摩擦定律,即摩擦力大小与法向接触力大小成正比,而方向与相对滑移速度方向相反:
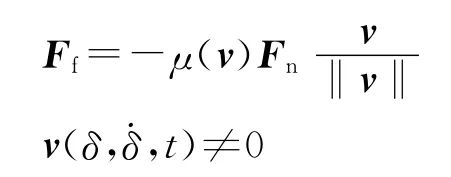
式中,Ff为接触处的滑动摩擦力;μ(v)为摩擦系数;接触点的相对滑移速度v(δ,,t)≠0.而粘滞状态的切向接触力与静摩擦系数有关.接触点处的运动量决定这2种状态的相互切换.
ADAMS中为了避免数值计算中速度方向变化时出现摩擦力突变,摩擦系数μ处理为与相对滑移速度v(δ,t)有关的变化曲线,其表达式为

式中,vs和vd分别为粘滞转换速度和动静摩擦转换速度,μs和μd分别为静摩擦系数、动摩擦系数,它们与两接触物体的材料属性以及表面粗糙度等因素有关.
2 多体系统动力学模型
2.1 虚拟样机模型
本文研究的导弹发射系统是一个复杂的动力学系统,为使仿真模型尽量简化而又真实、合理,将其简化为由导弹、发射筒、制导箱、方向机、高低机和发射基座等主要部分组成的多体系统,各部分之间的拓扑关系如图3所示.

图3 系统构件拓扑关系
利用UG建立系统的三维实体模型,确定构件间的初始位置及装配关系,并通过其与ADAMS的通用接口导入,建立虚拟样机模型进行动力学仿真分析,主要过程如下.
①整个系统包括弹体、发射筒、制导箱、方向机、高低机、发射基座等33个主要刚体,包括移动副、旋转副、圆柱副等在内的31个运动约束,包括弹与筒,筒与4个滑轨,筒与闭锁器,基座3个架腿与地面等18个接触碰撞力;
②发动机推力和燃气流后坐力通过实弹射击测得,形成6个AKISPL样条函数;
③方向机阻尼油的作用特性由一个作用力矩等效,力矩大小等于阻尼系数与相对回转角速度的乘积,力矩方向绕方向机的回转方向且与其运动角速度方向相反;
④1个传感器监测导弹运行过程,当导弹出筒时暂停仿真,输出结果;
⑤不考虑发射筒、弹体的不平度,不考虑加工误差引起间隙分布的随机性;
⑥不考虑射手在射击过程的作用力,即仿真过程为无控仿真.
2.2 接触参数的确定
该型号导弹系统的弹体与发射筒质量处于同一数量级.弹体定位块与发射筒的接触碰撞相当于圆柱体与圆筒碰撞,设δ0为弹筒间隙,导弹半径为r,发射筒内半径为R,R=r+δ0,则有:

将式(15)分别代入式(3)、式(5)、式(9)和式(14),得导弹与发射筒接触碰撞的动态接触刚度、阻尼系数和穿透深度.
试验射击时,发射系统置于水泥地面,基座支架腿与地面的接触面为弧形.因此将水泥地面看成一个曲率无穷大、质量无穷大的钢球,架腿与地面的接触碰撞相当于球形与球形的碰撞,且有:

将式(16)分别代入式(3)、式(4)、式(9)和式(14)得架腿与地面的动态接触刚度、阻尼系数和穿透深度.
类似地,计算其它接触碰撞力.在Adams中,碰撞力的类型选用“Solid to Solid”,利用Adams强大的几何搜索引擎判断几何体间的相对位置关系,接触发生后调用接触参数的计算程序,计算法向接触力和切向摩擦力.
3 动力学仿真分析
影响导弹初始扰动的因素很多,如导弹安装误差、发动机推力偏差、导弹的动不平衡、初始瞄准角、回转器阻尼特性等,且许多干扰量都具有随机性.为重点研究线性当量化的接触碰撞模型是否能较好地模拟系统的间隙接触问题,这里将各干扰量考虑成固定值,通过多次实验测量得到干扰量,并将其代入仿真模型进行模型验证.
3.1 仿真模型验证
以0°方向机初始方位瞄准角和2.5°高低机初始高低瞄准角的常温、室内、无控发射作为基本初始条件,弹筒间隙、导弹质心偏移、发动机推力及燃气流冲击力的轴向分力和径向偏差采用实验测量均值,将前面所述接触参数确定的方法代入该导弹发射系统的动力学模型中,仿真得到各构件的动力学响应曲线.将部分仿真结果与实验数据进行对比,列于表1中.表中,vr为导弹出筒速度,t为出筒时间,ωrx、ωry和ωrz分别为导弹的倾斜角速度、偏航角速度和俯仰角速度,αr、βr和γr分别为导弹的倾斜角、偏航角和俯仰角.表1中,实验值是多次室内常温无控发射实验所测得的导弹姿态的平均值.导弹出筒时的俯仰角、偏航角为负值,这表明导弹出筒时的姿态为低头右偏航,“—”表示无实测值.

表1 仿真结果与实验结果对比
由表1可知,仿真结果的导弹出筒姿态与多次实验的平均值很接近,说明用该模型来分析系统的动特性是可信的.
3.2 温度对初始扰动的影响
实验结果表明,发射温度的变化会对导弹的初始扰动产生影响.通过实验获取燃料燃烧在常温、低温和高温环境下对导弹产生的推力,并将实测结果输入到系统模型中,其它因素保持不变,计算得到不同温度下导弹运动姿态随时间的变化曲线,如图4所示.

图4 3种状态下导弹运动姿态变化曲线
从图4可以看出,高温发射时导弹出筒时间最短,低温发射时出筒时间最长.相比常温和高温状态,低温发射的导弹出筒倾斜角速度和俯仰角速度最大,偏航角速度更小.相比倾斜角速度和偏航角速度,由于俯仰角速度会受到导弹重力作用而下落,因此,俯仰角速度是需要重点关注的指标.综合来看,低温发射的初始扰动更大.不同温度造成不同的初始扰动,其本质为不同温度下的发动机推力及推力偏差不同,这和发动机推力偏差对导弹出筒扰动影响较大的结论是吻合的.
3.3 初始方位瞄准角对初始扰动的影响
导弹运动姿态随方向机初始方位瞄准角β0大小变化的部分仿真结果如图5所示.
其中,0°方位表示2条支架腿朝后且一条支架腿朝发射方向的布置方式,180°方位与其相反.180°布置方式的出筒倾斜角速度和俯仰角速度均大于0°布置方式.因此,选择3条支架腿布置方式时,2支架腿朝后且一条支架腿朝发射方向的方式更为合理.
同时,从仿真结果趋势来看,初始方位瞄准角在40°~60°之间,导弹俯仰方向初始扰动最大,但在360°方位射角内,导弹的出筒初始扰动幅值没有超过0.2rad/s,满足控制系统的稳定性要求.

图5 导弹出筒姿态随初始方位瞄准角的变化曲线
3.4 阻尼器特性对系统动特性的影响
制导箱是整个发射系统的重要部件,其运动特性将直接影响到导弹控制系统的稳定性,而方向机的阻尼器是为保证系统稳定性而设计的.图6~图8给出了方向机、制导箱和发射筒从导弹开始发射直到运动收敛至稳定时,各自的角速度曲线.图中ωh为方向机的回转角速度,ωf为制导箱的俯仰角速度,ωt为发射筒的俯仰角速度,ch为阻尼器的阻尼系数.

图6 方向机回转角速度运动曲线
图6表明,方向机在阻尼器作用下迅速收敛,且改变支架腿与地面的连接方式为固定连接时,方向机的初始扰动量大大减小.
图7表明,导弹发射出筒后,制导箱在初始激励下经过了约60ms收敛至0,支架腿与地面的固定连接方式使得制导箱初始扰动迅速减小.
同时,从图6、图7的对比曲线可以看出,阻尼器的阻尼系数对收敛速度影响不大,但对方向机以及与之相关的制导箱、发射筒等的回转角速度大小影响很大.从仿真结果来看,为满足战术指标要求,阻尼器阻尼系数在满足射手舒适性要求的情况下,应尽量大于300N·s/rad.
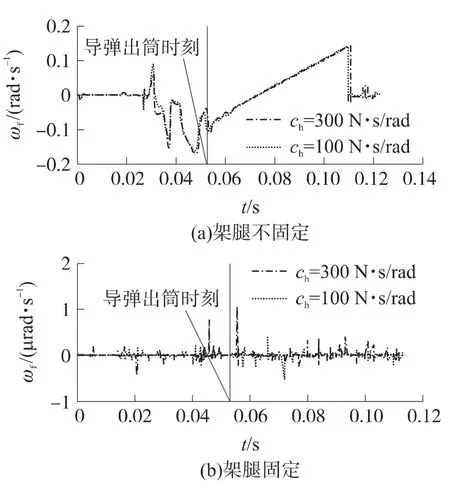
图7 制导箱俯仰角速度运动曲线
图8表明,在初始激励下,发射筒经过了约60ms收敛至0,支架腿与地面的固定连接方式减小了其初始扰动,但因为滑轨间隙的存在,仍然存在一定量的初始扰动,但增大了发射筒的运动收敛速度,系统稳定性更好.
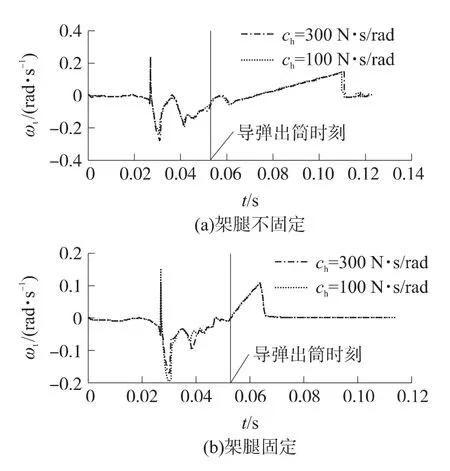
图8 发射筒俯仰角速度运动曲线
图9给出了支架腿不固定和固定2种情况下,导弹发射出筒过程的运动姿态曲线.从图9看到,固定支架腿的连接方式使导弹偏航和俯仰运动幅值更小,运动更平稳.
综合分析可知,增大架腿与地面的抓力可以增强系统的稳定性.实际战场运用时,由于有射手作用力的存在,射手利用身体施力于发射装置上也会使得系统的运动扰动减小,稳定性更好.
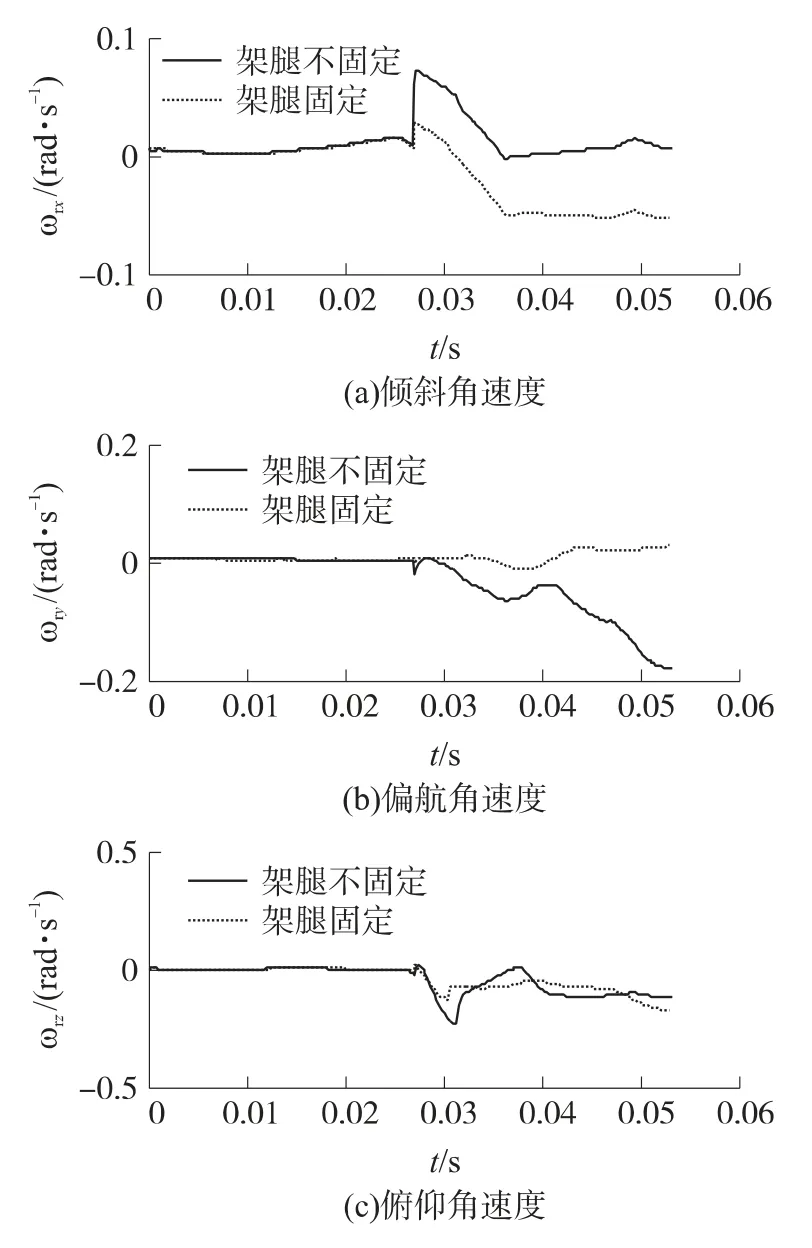
图9 导弹出筒过程运动姿态曲线
4 结束语
基于弹性理论,将考虑动态接触刚度、阻尼系数和穿透量的接触变形碰撞模型应用于某型号反坦克导弹发射系统的动力学建模中,借助ADAMS软件得到了系统的动力学响应结果.仿真结果基本符合试验结果,证明了该碰撞模型是有效的.
①不同温度引起不同发动机推力偏差,导致导弹初始扰动的变化,低温发射条件下的初始扰动较大.
②初始方位瞄准角对导弹初始扰动有影响,但仿真结果都满足战技指标.两腿朝后的布置方式优于两腿朝前的布置方式.
③方向机阻尼特性对系统稳定性有较大影响,阻尼器阻尼系数应在满足射手舒适性要求范围内尽可能大于300N·s/rad.
④支架腿与地面的连接方式对导弹系统的动特性有影响,增大支架腿的抓地力能使系统的初始扰动较小,稳定性增强.
通过对本文提出的模型进行仿真分析,可以得到发射系统在不同条件下的作战特性,这对该型号的武器系统性能分析和设计改进具有一定的参考价值.
[1]王志军,赵文宣.火箭弹起始扰动数值仿真研究[J].弹道学报,1996,8(3):69-74.WANG Zhi-jun,ZHAO Wen-xuan.Numerical simulation on the initial disturbance of rockets[J].Journal of Ballistics,1996,8(3):69-74.(in Chinese)
[2]DUBOWSKEY S,DECK J F.On the limitation of predictions of the dynamic response of machines with clearance connections[J].ASME J of Machine Design,1994,116:883-841.
[3]HUNTER S C.Energy absorbed by elastic waves during impact[J].J Mech Phys Solids,1957,5(1):162-171.
[4]马建敏,张文,郑铁生.转子系统瞬时撞击刚度的定量计算方法[J].应用力学学报,2003,20(2):68-71.MA Jian-min,ZHANG Wen,ZHENG Tie-sheng.Quantitative calculation method of instantaneous impact stiffness of rotor system[J].Chinese Journal of Applied Mechanics,2003,20(2):68-71.(in Chinese)
[5]徐振钦,马大为,乐贵高.基于碰撞接触的弹管多体动力学建模与仿真[J].系统仿真学报,2007,19(5):965-968.XU Zhen-qin,MA Da-wei,LE Gui-gao.Multibody dynamics modeling and simulation of rocket and launching tube based on contact-impact theory[J].Journal of System Simulation,2007,19(5):965-968.(in Chinese)
[6]ANAGNOSTOPOULOS S A.Equivalent viscous damping for modeling inelastic impacts in earthquake pounding problems[J].Earthquake Engineering and Structural Dynamics,2004,33(8):897-902.
