基于曲光线跟踪算法的超声成像实时模拟研究
2012-12-23陈思平汪天富
倪 东,陈思平,汪天富
医学超声关键技术国家地方联合工程实验室,广东省生物医学信息检测与超声成像重点实验室,深圳大学医学院,深圳518060
医学超声因具有无损、无辐射、实时、便捷等特点,被广泛应用于临床诊断、治疗和介入手术引导中. 在医学超声成像研究中,为优化超声探头设计,Jensen[1-3]提出一种用于任意形、不等指长换能器的脉冲压力场的模拟方法,在工业界和学术界均取得巨大成功. 该方法产生的超声模拟图像虽然较为逼真,但是往往需要几个小时才能产生一幅图像.
近年来,越来越多的研究者开始关注实时超声成像模拟,Maggie 等[4-5]提出从真实超声体数据中提取超声图像纹理来构建超声模拟图像. Henry[6]和倪东[7]等提出利用虚拟的超声探头,从已获取的宽视野三维超声数据中获取二维超声图像. 但是,构建宽视野三维超声数据需要鲁棒的图像配准和拼接算法,或者需要利用定位器来确定不同三维超声数据间的位置关系. Shams 等[8]提出通过合成离线获取的散射图和在线获取的反射图来获取超声图像,其中散射图通过Field II 软件获取. 这种方法的一个局限性是即使在一个有20 个CPU 的计算机服务器上,产生散射图也需约30 h. Song[9]提出用光线跟踪算法模拟声束,并用于心脏超声图像的模拟. 这种方法用理想化的光线模拟声束,光线不具有面积,降低了模拟图像的真实性. 文献[4-9]的另一个局限在于不能实时调整超声成像的重要参数,如声波频率和焦距. 但在实际超声扫查过程中,选择最优成像参数是一个重要的技巧.
斑点是由于声波的随机散射造成的,是超声成像的固有特性,在病理诊断中有一定作用. 但由于声波在人体内传输的复杂性,完全模拟超声斑点非常耗时. 近年已有研究利用不同的概率分布函数来描述超声斑点模式[10-14]. Johan[10]指出斑点可以点扩散函数来显示.
本研究提出一种基于曲光线跟踪算法的超声成像模拟新方法. 利用曲光线跟踪算法和基本声学模型,产生能量反射图和衰减图;用多条曲光线模拟聚焦声束,通过调整光线参数模拟声束频率和焦距的变化;运用瑞利概率分布函数产生超声斑点模式,并利用高斯型点扩散函数进行显示. 实验结果表明,该算法能满足实时模拟超声成像的要求.
1 声束聚焦模型
在现代超声成像系统中,探头孔径由一组阵元组成. 未聚焦的换能器形成的波束较宽,导致横向分辨率较低. 因此,声束聚焦技术被广泛应用于现代超声成像系统中. Christensen[15]指出声束在近场具有不规则形状,难以定义近场声束模型. 但在远场,声束轮廓随着距离的变化进行线性传播,并偏移固定的角度,如图1(a). 偏移角φd反比于探头直径D,正比于声波波长λ,定义为

文献[15]还指出聚焦区域横向分辨率与声束宽度相关,可近似为1.22λ/D. 提高声波频率可增加横向分辨率,超声图像质量与声波频率紧密相关,而在远场,超声图像因横向分辨率的降低而显得模糊. 基于以上声波传播的基本模型,本研究提出曲光线跟踪模型.
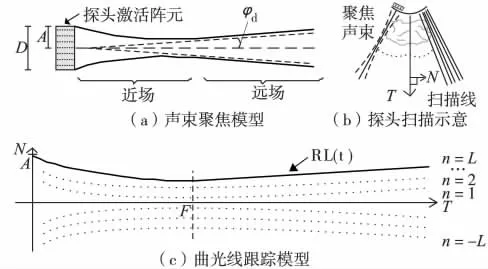
图1 声束聚焦及曲光线跟踪模型Fig.1 Illustration of the ray tracing model
2 曲光线模型
在传统光线跟踪模型中,理想光线用单个直线表示. 由于声束具有一定宽度及聚焦特性,我们提出用多条曲线模拟声束. 对于探头发出的每根扫描线如图1(b)均用多条曲线来模拟. 定义标量n 为曲线的标号,T 为探头扫描线的方向矢量,单位矢量N 为方向矢量的正交矢量,标量s 为声波传播距离,曲光线的方程定义为

其中,n = 0,±1,±2,…,±L;δn(s)是用于调整曲线形状的函数,可由式(3)计得,
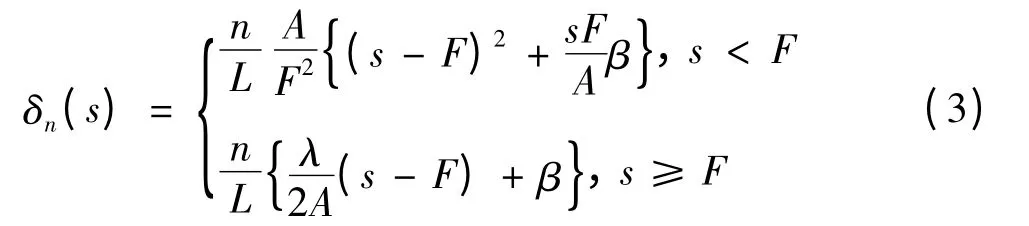
这里,A 是孔径;F 是焦距;L 是曲线在矢量T 两侧的最大个数;f 是声波频率;β 是用于控制曲线形状的常量.
以下分析式(2)和式(3)的物理特性. 设n= L 对应于图1(c)中最外面的一条曲线,当s <F时,随着传播距离s 的增加,通过控制β 值,δn(s)趋于最小值F,曲光线的曲率可由参数β 进行调整,与β 值成反比;当s ≥F 时,声束处于远场,将式(2)对s 求导数,求得曲线的斜率,即

因此,本研究提出的曲光线模型在近场是曲线,其宽度随着传播距离的增加而减小,而在远场是直线,直线的斜率与声束在远场的偏移角的正弦值相同. 在实际应用中,声束偏移角φd通常较小(<5°)[16],则

可见曲光线模型与声束聚焦模型一致. 在式(3)中,当s = F 时,δn(s)值最小,此时它就是声束聚焦处的宽度.


图2 曲光线跟踪模型示意图Fig.2 Illustration of different effects in ray tracing process
3 反射图模拟
图3 为为超声图像模拟示意图. 其中,图3(a)是合成的CT 图像,图3(b)是对目标光线跟踪得到的灰度图M,在此基础上,引入基本声学模型,计算能量反射图R 如图3(c)和衰减图S 如图3(d).
声波在传播过程中,由一种介质到达另一种介质,在两种介质的分界面上,由于声阻抗的不同,声波会发生方向和能量的变化:一部分声波被反射回原介质中,称为反射波;另一部分声波透过界面在另一种介质中继续传播,称为折射波. 这种现象将导致声波能量的衰减. 由于超声成像主要利用反射波检测信号,并且折射波的模拟非常困难和耗时[4],因此,本研究仅考虑声波的反射和由此引起的能量衰减.
声波反射与声阻抗密切相关. 声阻抗Z = ρc.其中,ρ 为介质密度;c 是声速. 声速在人体软组织中的传播速度约为1 540 m/s. 设声速为常数,声阻抗正比于组织密度. 利用文献[17]提出的CT图像亨氏单位(Hounsfield unit)与组织密度之间存在映射关系,可由图像灰度求取组织声阻抗,并根据声波能量反射系数公式(Z2-Z1)2/(Z2+Z1)2求得反射图.
声波衰减与声波所经过的组织和声波频率相关,文献[15]指出,声波能量I 随传输距离的变化呈指数衰减,即

其中,γ 是与组织性质相关的衰减系数;f 是声波频率;τ 是经验常数,本研究设τ = 1.

图3 超声图像模拟中间结果示意图Fig.3 Intermediate results
4 斑点模式模拟
斑点是超声图像由于声波随机散射造成的固有特性,在病理诊断中有一定作用. 但要完全从物理机制上模拟斑点模式是非常困难和耗时的,不适用于超声成像的实时模拟. 瑞利分布是描述超声斑点模式最常用的概率分布之一,我们采用瑞利概率分布函数产生超声斑点模式,并利用高斯型点扩散函数进行显示,起到平滑斑点噪声的效果. 为达到实时模拟的效果,斑点模拟和显示均用图形处理器(graphics processing unit,GPU)进行加速.
最终的超声图像模拟定义为
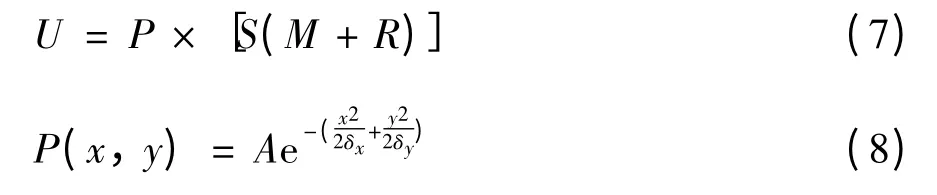
其中,S、M 和R 分别为能量衰减图、灰度图和反射图;P 为高斯卷积函数;A 为图像灰度值的瑞利概率分布值;δx和δy是高斯卷积函数的参数,分别对应横向分辨率和纵向分辨率. 超声图像模拟示意图见图3(e).
5 实验结果分析
为验证算法的可行性,我们对合成图像、解剖结构模型以及CT 图像进行了超声成像模拟,并比较了用不同的声波频率和聚焦位置获得的模拟结果. 图4 中的白色箭头表示焦距的位置.
首先,将自行合成的体模作为超声成像模拟的输入,图4(a)中(i)是分辨率体模图像,图4(b)中(i)是另一种体模图像. 图4(a)其他图像采用不同的声波频率对输入体模进行成像:(ii)为0.5 MHz,(iii)为1 MHz,(iv)为3 MHz. 结果显示,随着频率的增加,图像的横向分辨率得到提高,但由于高频率导致声波传输能量的衰减增多,灰度逐步变小. 图4(b)采用不同的声波频率和焦距进行成像:(ii)为0.5 MHz,1.5 cm;(iii)为0.5 MHz,3 cm;(iv)为1 MHz,3 cm. 从结果可见,随着频率的升高图像的横向分辨率得到提高,且在焦点位置的图像分辨率高于其他位置的图像.

图4 合成体模超声成像模拟图像Fig.4 Effect of acoustic frequency and beam focus on phantom data
为进一步说明本算法的可行性,将本研究结果与超声成像模拟的权威软件——Field II 生成的结果进行对比. 在文献[1] 中介绍了两种超声体模:肾脏体模和胎儿体模. 由于文献[1]将这两种体模描述为散射子的分布,我们首先基于解剖结构信息将散射子分布图转为灰度图,并将其作为超声成像模拟的输入. 图5(a)和图6(a)是Field II 软件的生成结果,在图5(b)中,由于声束聚焦位置在上端,下面的图像略显模糊,而图5(c)中,由于声束聚焦位置在下端的图像区域,则显示了较好的细节,图像也较清晰. 图(6)显示的是胎儿体模的超声模拟图,由于焦距的不同,图6(b)和图6(c)中的胎儿手指清晰度有较大差异.
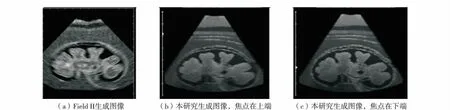
图5 肾脏体模超声成像模拟图Fig.5 Comparison of simulated kidney image

图6 胎儿体模超声成像模拟图Fig.6 Comparison of simulated fetus image
最后,我们将模拟结果与真实的超声图像进行了对比. 把一个实际的肝脏体模(CIRS Model 057)分别进行CT 成像和超声3 维成像,并将超声三维图像与CT 图像进行配准. 选取CT 图像的1 个切面作为超声成像模拟的输入,并将模拟结果与配准后相同位置的真实超声图像进行对比. 图7(a)是1幅CT 图像,图7(b)是用本算法产生的模拟结果,图7(c)是用超声扫描仪获取的真实超声图像,两者之间的相似性说明本算法可行.
另外,我们还对模拟成像的速度进行了评估.模拟软件在台式计算机上进行测试(CUP 为Penium 4 dual core 2,2.8 GHz;内存为2 Gbit;GPU 为Nvidia 8800). 通过采用GPU 对斑点的生成和显示进行加速,对于128 ×300 (128 根扫描线,每线300 个采样点)的超声图像,模拟成像速度可达约20 帧/s. 因此,本研究在超声引导下的虚拟手术和计划,超声诊断培训等方面有较好应用前景.

图7 肝脏体模超声成像模拟图Fig.7 Simulated ultrasound image from CT volume
结 语
本研究提出一种实时模拟超声成像的新方法,使用曲光线跟踪模型模拟声束,可实时调整声波的频率和焦点位置,同时利用概率分布函数产生超声斑点,并用GPU 进行加速显示. 将本研究算法产生的结果与Field II 软件和实际超声扫描仪获得的结果进行了对比,结果的相似性说明了本研究算法的可行性,本算法的速度也达到了实时性的要求.下一步,我们将基于声学理论,研究斑点噪声的概率分布模式、声波散射和折射现象的模拟,并研究临床病例CT 数据的超声成像模拟,最终将研究成果用于超声诊断培训、多模态图像配准以及超声引导下的虚拟手术等领域.
/References:
[1]Jensen J A. Field:a program for simulating ultrasound systems [J]. Medical & Biological Engineering & Computing,1996,34(1):351-353.
[2]Jensen J A,Gandhi D,O'Brien W D Jr. Ultrasound fields in an attenuating medium [C]// Proceedings of the IEEE Ultrasonics symposium. Vancouver (Canada):IEEE Press,1993,2:943-946.
[3]Jensen J A,Nikolov S. Fast simulation of ultrasound images [C]// Proceedings of the IEEE Ultrasonics symposium.Vancouver (Canada):IEEE Press,2000:1721-1724.
[4]Magee D,Zhu Y,Ratnalingam R,et al. An augmented reality simulator for ultrasound guided needle placement training [J]. Journal of Shenzhen University Science and Engineering,2007,45(10):957-967.
[5]Zhu Y,Magee D,Ratnalingam R,et al. A training system for ultrasound-guided needle insertion procedures[C]// Medical Image Computing and Computer-Assisted Intervention.Berlin:Springer,2007:566-574.
[6]Henry D,Troccaz J,Bosson J,et al. Ultrasound imaging simulation:application to the diagnosis of deep venous thromboses of lower limbs [C]// Medical Image Computing and Computer-Assisted Intervention. Berlin:Springer,1998:1032-1040.
[7]NI Dong,CHAN Wing-ying,QIN Jing,et al. A virtual reality simulator for ultrasound guided organ biopsy training[J]. IEEE on Computer Graphics and Application,2011,31(2):36-48.
[8]Shams R,Hartley R,Navab N. Real-time simulation of medical ultrasound from CT images [C]// Medical Image Computing and Computer-Assisted Intervention. Berlin:Springer,2008:734-741.
[9]Song M,Haralick R,Sheehan F. Ultrasound imaging simulation and echocardiographic image synthesis [C]//Proceedings of International Conference on Image.Vancouver:IEEE Press,2000:420-423.
[10]Johan M T. Speckle formation,analysis and processing applied to ultrasound tissue characterization [J]. Physics for Medical Imaging Applications,2007,240(3):151-176.
[11]Palhano Xavier de Fontes,Guillermo Andrade Barroso,Pierrick Coupé,et al. Real time ultrasound image denoising [J]. Journal of Real-time Image Processing,2011,6(1):15-22.
[12]Goodman J W. Some fundamental properties of speckle[J]. Journal of the Optical Society of America B,1976,66(11):1145-1150.
[13]CHEN Si-ping,ZENG Si-ning,WANG Tian-fu,et al.Numerical simulation on acoustic radiation force induced by ultrasonic coded excitation [J]. Journal of Shenzhen University Science and Engineering,2011,28(2):165-171.(in Chinese)陈思平,曾斯宁,汪天富,等. 超声编码激励产生声辐射力的数值模拟[J]. 深圳大学学报理工版,2011,28(2):165-171.
[14]Ogier A,Hellier P. A modified total variation denoisting method in the context of 3D ultrasound images [C]//Medical Image Computing and Computer-Assisted Intervention.Berlin:Springer,200:70-77.
[15]Christensen D A. Ultrasound Bioinstrumentation [M].1st ed. New York:John Wiley & Sons Inc,1988:89-112.
[16]Angelsen B A J,Waag R C. Ultrasound imaging:waves,signals,and signal processing [J]. Journal of the Acoustical Society of America,2007,121(4):1820.
[17]Wein W,Brunke S,Khamene A,et al. Automatic CTultrasound registration for diagnostic imaging and imageguided intervention [J]. Medical Image Analysis,2008,12(5):577-585.
