基于拓扑理论的超高速摄影仪转镜结构设计

李春波，余春晖，李景镇，柴金龙，刘春平，凌中水，黄虹宾，

1)深圳大学机电与控制工程学院，深圳518060;2)深圳职业技术学院汽车与交通学院，深圳518055;3)深圳市微纳光子信息技术重点实验室，深圳518060

在微秒级摄影领域，转镜式超高速摄影仪在成像的空间带宽积、实际动态范围、画幅数等主要摄影性能方面，优于电子类相机［1］，在爆轰物理、高电压放电、超音速风洞、激波物理、爆炸和碎裂、推进剂化学、细观和微观等超快过程现象记录等领域有着广泛应用［2］. 转镜作为超高速摄影仪中重要的光学加速部件，其动力学性能直接影响到摄影仪的工作可靠性、时间分辨率和空间分辨率.Дубовин А С［3］从理论力学和材料力学的角度求得转镜应力和变形量的计算公式. Трачук В С［4］将转镜复杂的3 维综合性力学问题转化为平面力学问题，推导出镜面变形量的二维解析解. 李景镇等［5-6］提出转镜强度计算的简化公式. 文献［7-8］提出在无制造缺陷的情况下，转镜的破坏是共振导致的疲劳破坏. 文献［9-15］总结出保证在实际运转中，转镜临界点出现在选定转速范围内的方法，研究和提出针对转镜动力学性能的结构设计方法.文献［16-18］在3 维有限元技术基础上对转镜镜面变形量进行深入研究，提出镜面变形量的几何补偿方法，并创造性地设计出蜂窝结构转镜.

转镜运转时在临界转速附近，尤其是在1 阶临界转速附近的振动现象，以及由此引发的潜在破坏是转镜设计面临的重要课题. 在保证转镜反射镜面尺寸不变的情况下，提高转镜的1 阶固有频率，一直是困扰转镜研究者的难题. 本研究基于连续体拓扑优化设计理论，提出转镜结构拓扑描述方式和材料插值模型，利用有限元分析软件ANSYS，以转镜基频为拓扑优化目标，转镜体积为约束条件，结合当前国内应用最广泛的大画幅和大画幅数铝转镜，在不改变转镜镜面尺寸前提下，进行最大动刚度拓扑的优化分析，并根据分析得到的转镜伪密度分布图对转镜结构进行修改，最后，对修改前后的转镜分别进行数值模态和试验分析. 研究发现，转镜1 阶固有频率由原来的713.6 Hz 提高到821.4 Hz，1 阶临界转速提高了15.1%，其他各阶固有频率也有显著提高;修改前后转镜模态数值解和试验结果的一致性证明转镜拓扑优化结果的正确性. 转镜的拓扑优化分析为转镜动力学性能的修改指出新的方向.

1 转镜拓扑优化分析原理

1.1 转镜拓扑优化插值模型

均匀化方法和变密度法是当前连续体拓扑优化的两个基本方法. 现有的主要密度插值模型包括材料属性的合理近似模型 (rational approximation of material properties，RAMP)［19］和固体各向同性惩罚微结构模型(solid isotropic microstructures with penalization，SIMP)［20-21］. 根据SIMP 方法，转镜材料插值模型的本质，是将转镜变量进行0 -1 离散后再对离散变量进行优化组合(0 表示该部分材料可以去除，1 表示该部分材料需要保留). 通过将转镜连续变量的密度函数显式地表达成离散化后单元相对密度与材料弹性模量间的对应关系，并以离散后转镜每个单元的相对密度作为设计变量，人为假定转镜相对密度和材料弹性模量间的伪密度对应关系，并通过引入惩罚因子对中间密度值进行惩罚，使中间密度值向0 -1 两端聚集，使连续变量的拓扑优化模型能很好地逼近0 -1 离散变量的优化模型. 在这种情况下，中间密度单元对应一个很小的弹性模量，对转镜刚度矩阵的影响很小. 基于上述方法，建立转镜材料插值模型［20］

其中，ρ(x)为转镜连续变量;Eijkl为单元初始弹性模量;E'

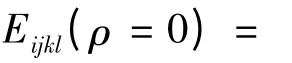
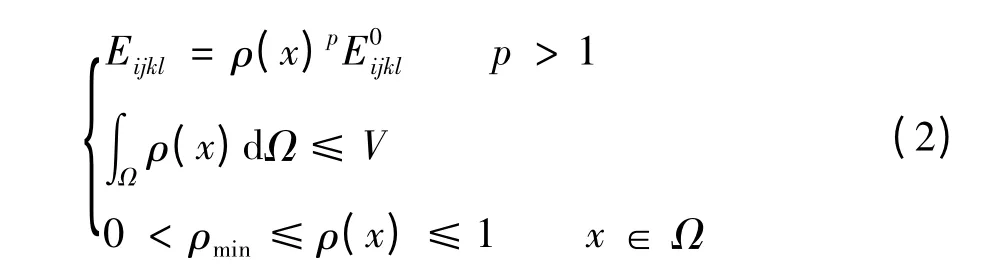
如果惩罚因子足够大，就能够得到无中间密度的优化区域. 对于3 维转镜，惩罚因子满足关系式［23］

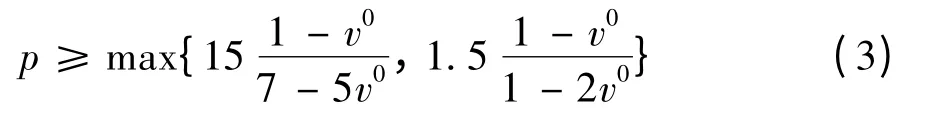
其中，v0为优化区域材料的泊松比. 转镜拓扑优化区域为镜体，材料为铝合金，泊松比0.3. 由于惩罚因子越大，中间密度就越小，故在转镜最大动刚度拓扑优化中，取惩罚因子为5.

1.2 优化算法

转镜拓扑优化模型建立后，需选择优化算法进行求解. 当前两类常用算法有优化准则法［22］(optimality criteria，OC)和序列规划法(sequential programming，SP). 本研究选择序列规划法中的凸规划法(sequential convex programming，SCP)对转镜拓扑优化模型进行求解. 该方法的基本思想是在求解过程中采用一系列简单的问题来逐步逼近复杂问题，通过相关转化，将转镜最大动刚度的求解转化为一个较低阶次的非线性或线性问题渐近求解. 根据拓扑优化理论［22-25］，建立转镜拓扑优化数学模型

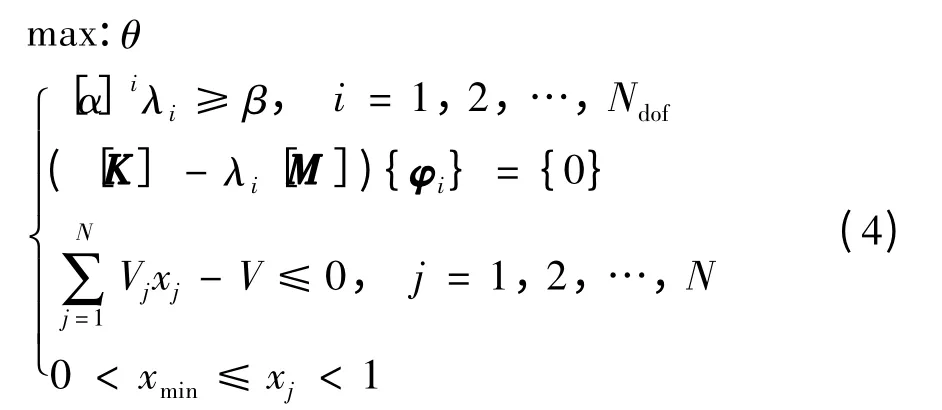
其中，θ 为优化目标，即转镜第1 阶固有频率;［K］为转镜刚度矩阵;［M］为转镜质量矩阵;{φi}为第i 阶特征值λi对应的转镜模态;x 为转镜设计变量. 为避免刚度矩阵中出现奇异矩阵［23］，取xmin=0.001;V 为优化后的转镜体积;Vj为第j 个单元的体积;j = 1，2，…，N 为转镜优化区域内的单元数目;i = 1，2，…，Ndof为对应的转镜模态数目. 在对转镜模态和谐响应分析［12-13］中发现，对转镜动力学性能影响最大的主要是转镜的前几阶模态，故提取转镜模态数为10，α 取0.95［22-25］.

优化分析转镜最大动刚度拓扑，使转镜1 阶固有频率对应的临界转速高于转镜的工作转速. 最大动刚度拓扑优化就是使转镜的基频最大，故目标函数为

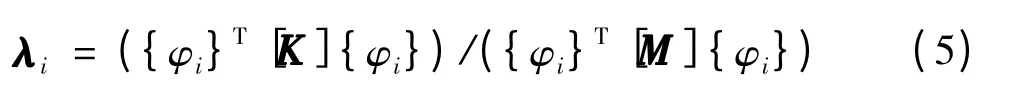
其中，λi为转镜阶特征向量;{φi}T为转镜i 阶振型向量的转置. 最大动刚度拓扑优化就是求解式(5)的最大值.

2 数值分析

转镜最大动刚度拓扑优化的目标，是转镜在承受单载荷或多载荷约束条件下，寻求最佳材料分配或最佳传力路径的方案，使其1 阶固有频率在满足给定实际约束条件下，通过减小结构的变形能，即提高转镜结构刚度，使其达到设计所需的极大值.与传统的优化设计相比，转镜拓扑优化最大的不同是不需要给出参数和优化变量定义，目标函数、状态变量和设计变量都已根据结构设计的要求自行预定好，只需要给出结构的材料特性、模型、载荷和要省去的材料百分比.

2.1 转镜最大动态刚度拓扑优化分析模型

转镜最大动刚度拓扑优化设计数值分析的基础是转镜的模态分析，即将转镜固有频率作为拓扑优化的目标函数. 由于1 阶固有频率(即基频)对转镜的动态特性影响最大，故转镜最大动态刚度拓扑优化设计数值分析，直接以转镜1 阶固有频率作为优化的目标函数，进行单模态拓扑优化分析.

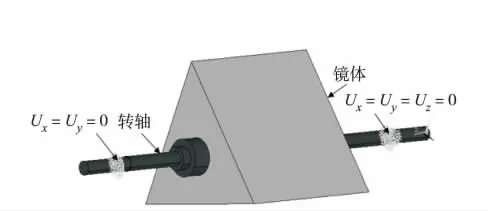
图1 原转镜模型Fig.1 The original model of rotating mirror

图1 为原转镜模型，转镜由镜体和转轴两部分构成，两者经过盈配合连接. 转轴材料为45 钢，经调质、淬火处理，弹性模量210 GPa，泊松比0.26，密度7 800 kg/m3. 镜体选用铝合金，弹性模量71.7 GPa，泊松比0.33，密度2 780 kg/m3. 采用单列深沟球轴承支撑，一端为固定铰支，另一端为活动铰支. 由于转镜镜面变形量对时间分辨率的影响大，故将镜体表面0.2 mm 的厚度和转轴材料定义为非优化的区域. 定义转镜1 阶固有频率作为拓扑优化目标函数，拓扑优化区域体积为拓扑优化约束条件，选择序列凸规划法进行转镜的最大动刚度拓扑优化数值分析. 通过多次反复取值进行数值分析和试验发现，选择体积减少30%进行迭代运算，转镜综合力学性能最好. 图2 ～图4 为转镜拓扑优化分析结果.

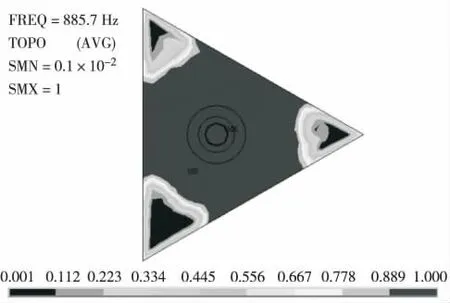
图2 伪密度分布图Fig.2 Pseudo-density distribution

图3 目标函数迭代曲线Fig.3 Iterative curve of objective function

图2 为转镜伪密度分布图，转镜优化区域中3个尖角部分中间密度值约为0.001. 为避免转镜模态分析中刚度矩阵出现奇异，对转镜拓扑优化区域优化变量取xmin=0.001，故该部分伪密度值可视为0，该部分材料可以删除. 目标函数迭代曲线(图3)和约束条件迭代曲线(图4)经过初期波动后趋于水平，说明转镜最大动刚度拓扑优化数值分析结果收敛. 图2 和图3 显示，转镜最大动刚度拓扑优化的1 阶固有频率收敛解为885.7 Hz.

图4 约束条件迭代曲线Fig.4 Iterative curve of constraint condition

3 转镜结构优化

根据转镜拓扑优化得到伪密度分布图，删除伪密度值小的材料区域，对镜体结构形状进行拓扑优化. 图5 为修改后新转镜镜体的3 维模型. 相比于图1，图5 的转镜外形结构只去除了优化区域伪密度值较小的部分，其他结构尺寸不作修改. 然后对修改前后转镜在相同约束条件(图1)下进行模态分析［9-15］.

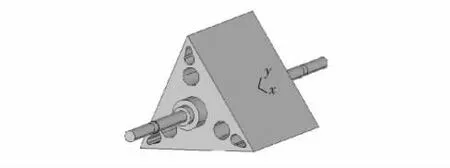
图5 转镜新模型Fig.5 New model of rotating mirror

表1 为结构修改后转镜模态数值分析，以及原有结构转镜模态分析前5 阶模态结果的对比. 转镜优化后第1 阶模态值为821.4 Hz. 由于优化得到转镜伪密度图形中位密度值为0 的单元为非均匀分布，实际中不可能将拓扑优化结果中伪密度值为0的材料完全去除;且由于中间伪密度值的存在，一部分保留的转镜镜体单元伪密度值不为1，这是新转镜的基频比转镜最大动刚度拓扑优化得到的收敛解要小的原因. 由表1 还可知，转镜第1 阶模态固有频率值增加了107.8 Hz，变化率为15.1%，说明转镜最大动刚度拓扑优化数值分析的基频值是正确的.

由于大画幅超高速摄影仪要求转镜反射面大，这就使得转镜体积较大. 转镜工作转速很高，前几阶固有频率对应的临界转速低于转镜的工作转速，转镜在加速或减速过程中跃过共振点时，如果在低阶固有频率的共振带停留时间较长，会因出现共振而被破坏，对摄影仪的工作可靠性产生直接影响.通过对拓扑优化后的转镜进行模态分析和试验发现，在相同镜面尺寸下，新转镜的1 阶固有频率相对原转镜增加15.1%，第2 阶固有频率增加48%，第3 阶固有频率增加50%. 转镜最大应力由原来的5.38 MPa 增加到5.47 MPa，转镜的静强度有轻微降低，但仍满足设计要求. 因此通过对转镜基频进行最大动刚度拓扑优化分析，使转镜各阶固有频率都得到很大程度的提高. 这对大画幅转镜的动力学设计提供了可靠有效的设计思路.

表1 模态分析结果对比Table 1 Contrast of model analysis results

4 试验分析

转镜模态实验分析系统如图6. 采用WS-5932综合信号采集系统和Vib' SYS 分析软件，该测试系统直接以电机驱动，通过信号采集系统在线测量转镜加速度响应信号，经A/D 转换为时域响应信号，再通过FFT 变换加Hanning 窗过滤时域信号中的噪声后，得到转镜幅频响应曲线，最后通过Vib’SYS 软件的图像处理功能输出转镜幅频响应曲线.图7 和图8 分别为原转镜和新结构转镜在1 阶固有频率处的频域响应曲线. 由图7 可见，原转镜在714.5 Hz 处开始出现峰值，即1 阶固有频率为714.5 Hz，图8 表明新转镜的1 阶固有频率为823.4 Hz. 考虑到试验结果和数值解之间存在不可避免的误差，因此，可认为优化前后转镜的模态分析结果是正确的. 数值解和试验结果的一致性说明，通过对已有结构进行最大动刚度拓扑优化，转镜1 阶固有频率有很大提高.

图6 转镜试验测试系统程序框图Fig.6 The block diagram of rotating mirror test system

图7 原转镜幅频响应曲线Fig.7 The frequency-amplitude characteristic curve of original rotating mirror

图8 新转镜幅频响应曲线Fig.8 The frequency-amplitude characteristic curve of new rotating mirror

结 语

基于连续体拓扑优化设计理论，利用有限元法及ANSYS 软件，建立转镜各向同性惩罚微结构单模态拓扑优化插值模型，对转镜的1 阶固有频率进行最大动刚度拓扑优化数值分析，并根据转镜伪密度分布图，修改原有转镜结构. 对修改前后的转镜进行模态数值分析和试验. 通过对比两转镜的结果发现，在不改变转镜反射面尺寸的前提下，转镜的1 阶固有频率增加了107.8 Hz，变化率为15.1%.其他各阶固有频率亦有显著提高，第2 阶模态值增加48%，第3 阶模态的数值增加50%. 试验结果和数值解一致，为有效提高转镜的动力学性能，在不改变转镜镜面尺寸前提下修改转镜固有频率点的位置，提供了新的设计思路和方法.

/References:

［1］Frank A M，Bartolick J M. Solid state replacement of rotating mirror camera ［C］// The 27th International Congress on High Speed Photography and Photonics. Xi'an:SPIE Press，2007:62791U-627910U .

［2］Jong N，Chin C T，Lancee C，et al. A rotating mirror digital camera with 128 frames at 25 Mfps ［C］// The 25th International Congress on High-Speed Photography and Photonics. Beaune (France):SPIE Press，2003:3472-3477.

［3］Дубовин А С. Photographic Record of High-speed Passing Process ［M］. LI Xiong，XI Guang-si，translate. Beijing:Science Press，1976:25，57-69.(in Chinese)Дубовин А С. 高速流逝过程摄影记录［M］. 黎雄，西光四，译. 北京:科学出版社，1976:25，57-69.

［4］Трачук В С. Elastic distortion of high-speed rotating mirror ［J］. Scientific Photography，1977，22(5):335-342.

［5］LI Jing-zhen，SUN Feng-shan，GONG Xiang-dong，et al.Study on dynamic behavior of rotating mirror ［C］// The Conference on Advanced Sensor Systems and Applications II. Beijing:SPIE Press，2005:117-123.

［6］LI Jing-zhen，Sun Feng-shan. Dynamic property of rotating mirror of high intensity aluminium alloy for ultra high speed photography ［J］. Acta Photonica Sinica，2000，29(5):636-639.(in Chinese)李景镇，孙凤山. 超高速摄影用高强度铝合金转镜动态特性的研究［J］. 光子学报，2000，29(5):636-639.

［7］HUANG Hong-bin，LI Jing-zhen，SUN Feng-shan ，et al.Numeric analysis of structural of aluminous alloy rotating mirror for ultra-high speed photography ［J］. High Power Laser and Particle Beams，2006，18(8):1277-1280.(in Chinese)黄虹宾，李景镇，孙凤山，等. 超高速摄影中三面体铝合金转镜的空间结构强度数值分析［J］. 强激光与粒子束，2006，18(8):1277-1280.

［8］LI Chun-bo，YU Chun-hui，CHAI Jin-long. et al. Fatigue research for rotating mirror of ultra-high speed camera through numerical analysis and experimental methods［C］// Special Event of the International Symposium on Photoelectronic Detection and Imaging. Beijing:SPIE Press，2011:81910P1-81910P8.

［9］HUANG Hong-bin，CHAI Jin-long，LI Jing-zhen，et al.Mechanical analysis on beryllium rotating mirror of ultrahigh speed camera ［J］. Joural of Shenzhen University Science and Engineerng，2007，24(2):122-125. (in Chinese)黄虹宾，柴金龙，李景镇，等. 超高速摄影中铍转镜静力学与动力学性能分析［J］. 深圳大学学报理工版，2007，24(2):122-125.

［10］HUANG Hong-bin，LI Jing-zhen，SUN Feng-shan，et al.Numerically simulating the static property for rotating mirror of ultra-high speed camera ［J］. Journal of Shenzhen University Science and Engineering，2007，24(1):75-78.(in Chinese).黄虹宾，李景镇，孙凤山，等. 超高速摄影中转镜力学特性的数值模拟［J］. 深圳大学学报理工版，2007，24(1):75-78.

［11］YU Chun-hui，LI Chun-bo，LIU Chun-ping，et al. Numerical and experimental research for dynamic sensitivity of rotating mirror of ultra-high speed camera ［C］// Special Event of the International Symposium on Photoelectronic Detection and Imaging. Beijing:SPIE Press，2011:81910Q1-81910Q8.

［12］LI Chun-bo，YU Chun-hui，CHAI Jin-long，et al. Modal analysis through numerical and experimental methods for rotating mirror of ultra-high speed camera ［J］. Journal of Shenzhen University Science and Engineering，2011，28(6):513-517.(in Chinese)李春波，余春晖，柴金龙，等. 超高摄影仪转镜模态的数值分析与实验分析［J］. 深圳大学学报理工版，2011，28(6):513-517.

［13］YU Chun-hui，LI Chun-bo，LIU Chun-ping，et al. Dynamic researches for rotating mirror of ultra-high speed camera ［J］. Acta Photonica Sinica，2011，40 (7):1013-1019.(in Chinese)余春晖，李春波，刘春平，等. 超高速摄影仪转镜动力学性能的研究［J］. 光子学报，2011，40(7):1013-1019.

［14］HUANG Hong-bin，LI Jing-zhen，GONG Xiang-dong，et al. Modal analysis of rotating mirror clipped by the elastic bearings for ultra-high speed photography ［J］. High Power Laser and Particle Beams，2007，9(2):225-228.(in Chinese)黄虹宾，李景镇，龚向东，等. 超高速摄影中弹性支撑转镜的模态分析［J］. 强激光与粒子束，2007，19(2):225-228.

［15］LI Chun-bo，YU Chun-hui，CHAI Jing-long，et al. Design of rotating mirror for ultra-high speed camera based on the dynamic characteristic ［J］. High Power Laser and Particle Beams，2011，23(12):3395-3399.(in Chinese)李春波，余春晖，柴金龙，等. 基于动力学性能的超高速摄影仪转镜的设计［J］. 强激光与粒子束，2011，23(12):3395-3399.

［16］HUANG Hong-bin，CAI Jin-long，GONG Xiang-dong，et al. Advance deforming mirror faces of rotating for streak camera ［J］. Acta Photonica Sinica，2008，37 (5):1015-1018.(in Chinese).黄虹宾，柴金龙，龚向东，等. 扫描式超高速摄影中转镜镜面变形量的几何补偿［J］. 光子学报，2008，37(5):1015-1019.

［17］HUANG Hong-bin，LI Jing-zhen，HUI Bin，et al. Mechanical and optical performance analysis on rotating mirror with honeycomb cellular structure in ultra-high speed camera ［J］. Journal of Shenzhen University Science and Engineering，2008，25(2):163-167.(in Chinese)黄虹宾，李景镇，惠 彬，等. 超高速摄影中蜂窝结构转镜性能分析［J］. 深圳大学学报理工版，2008，25(2):163-167.

［18］HUANG Hong-bin，CAI Jin-long，LI Jing-zhen，et al.Design and mechanical analysis on rotating mirror with honeycomb cellular structure in ultra-high speed camera［J］. High Power Laser and Particle Beams，2008，20(3):363-366.(in Chinese)黄虹宾，李景镇，柴金龙，等. 超高速摄影中蜂窝结构转镜的设计与力学分析［J］. 强激光与粒子束，2008:24(3):363-366.

［19］Stolpe M，Svanberg K. An alternative interpolation scheme for minimum compliance topology optimization ［J］. Structural and Multidiscipline Optimization，2001，22(2):116-124.

［20］Rozvany G I N，Kirsch U，Bendsoe M P，et al. Layout optimization of structures ［J］. Applied Mechanics Reviews，1995，48:41-119.

［21］Rietz A. Sufficiency of a finite exponent in SIMP (power law)methods ［J］. Structural Multidiscipline Optimization，2001，21(2):159-163.

［22］LUO Zhen，CHEN Li-ping，HUANG Yu-ying，et al. Topological optimization design for continuum structures［J］. Advances in Mechanics，2004，34(4):463-476.(in Chinese)罗 震，陈立平，黄玉盈，等. 连续体结构的拓扑优化设计［J］. 力学进展，2004，34(4):463-476.

［23］Pederson N L. Maximization of eigenvalues using topology optimization ［J］. Structural and Multidiscipline Optimization，2000，20(1):2-11.

［24］Seyranian A P，Lund E，Olhoff N. Maximization of eigenvalues using topology optimization ［J］. Structural Optimization，1994，8(4):207-227.

［25］ZUO Kong-tian. Research of Theory and Application about Topology Optimization of Continuum Structure ［D］. Wuhan:Huazhong University of Science and Technology，2004:16-30.(in Chinese)左孔天. 连续体结构拓扑优化理论与应用研究［D］.武汉:华中科技大学，2004:16-30.