竖向排水体地基下的轴对称及平面应变模型分析
2012-12-23徐耘野李光范骆俊晖
徐耘野,李光范,骆俊晖
(海南大学土木建筑工程学院,海南海口 570228)
竖向排水体地基下的轴对称及平面应变模型分析
徐耘野,李光范,骆俊晖
(海南大学土木建筑工程学院,海南海口 570228)
基于在实际工程中对竖向排水的三维建模比较困难,常常使用二维的平面等效应变模型进行分析.本文中根据不同的条件,分析了不同的二维平面应变模型.通过数值分析,对参数(n=re/rw,s=re/rs,η=kh/ ks)进行了研究,以确定影响因素.结果显示,Hird的模型体现了良好的整体适用性.对于密实沙桩需要用不同的方法来进行有限元分析,需要考虑砂井中排水因素的刚度,同时还要考虑等效排水宽度.结果表明,在交叉区域,等效平面应变模型可以比三维分析模拟现场沉降更好.
竖向排水;平面应变;有限元
通过使用竖向排水,减少排水距离,可以加快土初始固结的速度.因此,竖向排水常常被用在软土地基上,以加快土的初始固结.使用竖向排水,主要有以下几个目的:
1)增加土的排水抗剪强度,加快土的快速固结;
2)减少预压时间来降低施工后的沉降;
3)在初始固结阶段减少不均匀沉降;
4)减少大量的附加条件,在一定时间内达到一定的预压量.
传统的解决方案只适用于单向排水分析,而对于多向排水的分析则需要其他的方法.虽然在沿路堤中线的土壤的性能上,单向排水的分析往往就足够了,但是若是需要考虑沿路基宽度方向的重力荷载变化的影响,并准确地预测沉降和侧向位移时,多向排水的分析就是必不可少的.为了分析多向排水,就需要一个能模拟原位固结性质的三维轴对称模型[1].然而,在三维分析中有很多的困难,而且需要大量的时间.因此,处于原位状态的实际三维模型,可以通过使用一些等效模型,转换成等效的二维平面应变模型.
1 研究现状
1.1 竖向排水的理论 Rendulic(1935)提出了在径向排水情况下一维垂直压缩的微分方程

式中,ch(=kh/(γwmv))是水平固结系数.
Carillo(1942)提出了在一维压缩的情况下,纵向和径向流动的超孔隙水压力ur,z的求解方程.

式中,cv(=kv/(γwmv))是垂直固结系数,ur是只有径向流动时候的超孔隙水压力,uz是只有纵向流动时候的超孔隙水压力.

Barron(1948)提出的固结理论,包括了涂抹效应和阻力的影响,他利用太沙基固结理论作为如下基本假设:
1)所有垂直荷载的初始超孔隙水压力都为u;
2)土体中所有压缩应变都发生在一个垂直方向;
3)考虑在地基上的任何一点的载荷分配和每个井固结速率的影响;
4)每个井的影响的区域是一个圆;
5)对这个区域的载荷分布是均匀的.
在这5个基本假设的前提下,Barron提出了自由应变的边界条件,等效的垂直应变,考虑了涂抹效应,最终提出了竖向变形和土体平均固结度的微分方程.
1.2 二维的竖向排水模型 到目前为止,在所有对竖向排水井地基的分析方法中,当所分析的单向排水影响的区域为一个圆形区域时,都采用了“单元”这样一个概念.对“单元”做了以下假设:每一个单元独立工作,所有的变形都只发生在土体内部的垂直方向[2-3].然而,由于假设中没有侧向位移,所以在实际工程中很有可能出现不稳定,因此,将竖向排水看成一个三维问题似乎更为合理.然而,在三维条件下,对竖向排水的离散模型的有限元计算将使得常规分析变得十分复杂[4],因此,二维模型的分析更实际.所以,在固结分析的时候,需要将实际情况中的三维空间的排水转化为二维的平面应变模型来进行分析.Shinsha (1982),Bergado(1994),Hird(1992),Lee(1997)等人都提出了自己的二维平面应变模型.
1.2.1 Bergado的模型在Bergado的模型中,考虑了涂抹效应对渗透性的影响,而且假设在渗流状态下,渗透系数是相互独立[5].

1.2.2 Hird的模型在平面应变的情况下,Hird根据Hansbo的理论,提出在2个单元内,在任何时间和任何深度下的平均固结度U在理论上都是相同的[6].Hied等人提出了下面3个条件方程[7]:

除了以上2种模型外,还用Cheung,Shinsha,Lee等模型来研究二维的竖向排水.本文主要对Bergado模型和Hird模型进行了研究.
2 数据分析结果
3.1 等效平面应变模型的比较
3.1.1 模型特性分析模拟100 kPa的速率加载,观察其瞬时应变.为了构建有限元分析模型,使用弹性模型来模拟粘土地基和排水管,输入参数详见表1,有限单元网格如图1所示.
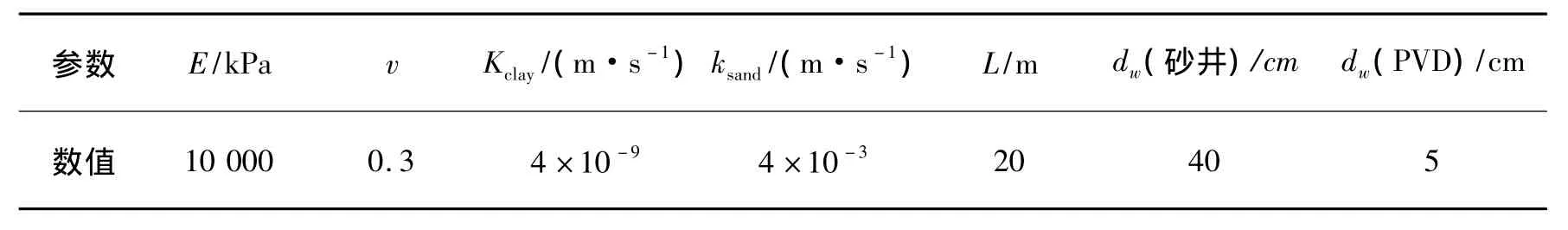
表1 模型特性的输入参数

图1 单元分析的有限元网格
3.1.2 涂抹效应确定了涂抹区之后对其进行数值分析,通过轴对称模型分析出平面应变模型的作用.

图2 比较t50时的考虑涂抹效应的区域地基,n=8

图3 比较t90时的涂抹效应,n=8

图4 比较U50时所用的时间

图5 比较U90时所用的时间
假设n=re/rw=8,dw=0.5 m,de=4 m,涂抹区的参数比排水井参数大1~5倍,其渗透性在1/2和1/5之间.图2和图3是n,re/rw和kh/ks不同取值时的影响(以n=8时为例).3.1.3不同n=re/rw取值下等效模型对比在砂井中,排水井的参数为40 cm,其n的值分别取5,8,12,20;而预制竖向排水井的参数是0.05 cm,n的取值分别为20,30,40.分析时,除了用Hird模型和Bergado模型外,同时也采用Cheung模型、Shinsha模型和Lee模型分别对U50和U90的所用时间进行研究,如图4和图5所示.
从图4和图5可看出,通过轴对称比较分析的结果,可以得到以下结果:
1)U50所用时间的比较
①砂井(n取值从5~20):

②预制垂直排水井(n取值从20~40):

2)U90所用时间的比较
①砂井(n取值从5~20):

②预制垂直排水井(n取值从20~40):

3.2 固结分别达到50%和90%所用时间的修正方程 假设涂抹区参数和涂抹区渗透性是连续的,对于Hird模型和Bergado模型,可以通过n的赋值得到下列修正方程.

其中:对于Hird模型(5≤n≤40),a1=-88.00,b1=18.60,a2=-57.25,b2=15.61;对于Bergado模型(5≤n≤40),a1=-66.63,b1=3.31,a2=-29.91,b2=4.10.
3.3 三维分析 用有限元分析软件ABAQUS进行3D分析,以分析排水系统中的交叉影响.

图6 三维网格单元图

图7 等效的三维分析
为了能够利用ABAQUS(版本5.8)中的8节点立方体单元将砂井理想化为相兼容的单元,把每一个砂井的圆截面转化为同等面积的方形面.3D分析中排水地基进行有限元理想化的概念可以参见图6,7.以n=5为例,将交汇区域的沉降和超孔隙水压力的模拟结果作图,如图8和图9所示.
3.4 考虑排水刚度的结果 倘若竖向排水井这类排水管道刚度是可以忽略的排水系统,Hird模型能够很好地预测其固结性状,那么,当要预测排水砂桩或是挤密砂桩这类刚度较大的排水系统时,就需要考虑排水井刚度这一因素.因此,平面应变模型中垂直排水管的宽度,可以通过同时在轴对称模型和平面应变模型中考虑排水管道刚度来加以调整.结果见图10和图12.

图8 交汇区域的沉降,n=5

图9 交汇区域的超孔隙水压力,n=5

图10 沉降随排水刚度的变化

图11 修正排水宽度的沉降比较
3.5 现场数据的应用(Seochon) 在SC-A区域,要安装袋装砂井(dw=12 cm,S=3.1 m),而在SC-B区域,则要安装塑料排水板(dw=5 cm(排水等效半径,Hansbo),1.3 m).袋装砂井是砂井的一种,它具有排水刚度.随着时间的流逝,砂井的刚度可能会减缓固结的速度,因此有必要考虑排水刚度,从而能够更加准确地模拟现场性状[8].结果见图12,13和表2.

图12 仪器截面SC-A(Cho,1998)

图13 路堤沉降和荷载曲线关系(SC-A)

表2 MCC模型有限元分析
4 结 论
本文通过对不同平面应变模型的参数研究,再加上采用ABAQUS进行3D分析,得出了如下结论:
1)总体上看,可以利用平面应变模型来预测固结性状;
2)可以使用修正方程来预测弹性模型中固结度为50%和90%时的运行时间;
3)在模拟砂井和密实砂桩时,要考虑到刚度的影响,对排水管道的等效宽度进行修正;
4)对于交叉区域,等效平面应变模型能够比3D模型更好地模拟现场处理;
5)尽管在估算特定区域的超孔隙压力上还存有一定的局限性,但是平面应变模型完全可以应用于垂直排水管的设计实践中.
[1]蒋春霞.含竖向排水体地基固结变形问题研究综述[J].山西建筑,2008,34(34):121-122.
[2]BARRON R A.Consolidation of fine-grained soils by drain wells[J].Transactions of the American Society of Civil Engineers,1948,113:718-742.
[3]HANSBO S.Consolidation of fine-grained soils by prefabricated drains Proceedings of 10th International Conference on Soil Mechanics and Foundation Engineering,Stockholm,June 15-19,1981[C].Stockholm:Balkema A A,Rotterdam,1982.
[4]秦道标.含竖向排水体的软土路基固结分析[J].山西建筑,2009,35(6):279-280.
[5]BERGADO D T,LONG P V.Numerical analysis of embankment on subsiding ground improved by vertical drains and granular piles Proceedings of 13th International Conference on Soil Mechanics and Foundation Engineering,New Delhi,January 5-10,1994[C].[S.l.]:Taylor&Francis,1994.
[6]HIRD C C,PYRAH I C,RUSSELL D.Finite element modelling of vertical drains beneath embankments of soft ground[J].Geotechnique,1992,42(3):499-511.
[7]HIRD C C,PYRAH I C,RUSSELL D,et al.Modelling the effect of vertical drains in two-dimensional finite element analysis of embankments on soft ground[J].Can.Geotech.J,1995,32:795-807.
[8]蒋春霞.含竖向排水体地基轴对称固结及平面应变等效固结分析[D].江苏:河海大学,2005.
Axisymmetric and Plane Strain Model Analysis of Foundation with Vertical Drainage Body
XU Yun-ye,LI Guang-fan,LUO Jun-hui
(College of Civil Engineering and Architecture,Hainan University,Haikou 570228,China)
Due to the difficulties of modeling with three dimensional(3-D)axisymmetric multidrain systems,equivalent plane-strain analysis has generally been used.In this paper,based on the different conditions,the evaluation of various two-dimensional(2-D)plane-strain models were conducted to find appropriate models.Parametric were studied to determine influencing factors(n=re/rw,s=re/rs,η=kh/ks)via numerical analysis.The results suggested that Hird’s model showed a good overall match.Sand Compaction Pile(SCP)required different methodologies for the finite element analysis of vertical drains,and it was necessary to consider the stiffness of drain elements in sand drains and the equivalent drainage width.In the intersection zone,the effects of simulating field settlement of plane strain models were better than that of 3-D analysis.
vertical drains;plane strain;FEM
TQ 639.2
A
1004-1729(2012)01-0048-06
2011-09-20
徐耘野(1986-),男,贵州安顺镇宁人,海南大学土木建筑学院2009级硕士研究生.
李光范(1959-),男,海南大学土木建筑学院教授,博士.
