关于有限个超越整函数迭代的若干性质
2012-12-22俞蕴妮
俞蕴妮, 洪 霞
(1.南昌师范高等专科学校 自然科学系, 江西 南昌 330029; 2.江西电力职业技术学院 信息系, 江西 南昌 330032)
Hinkkanen和Martin[1-2]研究了由一族有理函数{h1,h2,…,hn,…}生成的一个半群H的动力系统,其中半群算子是函数的复合.与古典Fatou-Julia理论相似地定义了半群H的Fatou集和Julia集,并得到与古典理论极为相似的一些动力性质.后来,关于这方面有着很多的研究,如Sumi[3],Poo[4],Huang[5].
设H是一个由一族超越整函数{h1,h2,…,hn,…}生成的一个半群,其中半群算子是函数的复合.定义H的Fatou集为F(H)={z∈C|H在z的某个邻域上正规}以及H的Julia集为J(H)=CF(H).同时,对于z∈C,定义O-(z)={ω∈C存在一个g∈H满足g(ω)=z}以及H的例外点集E(H)={z∈C︱O-(z)是有限的}.
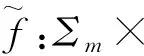
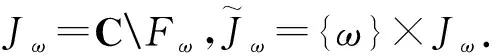
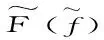
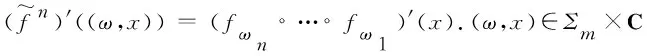

Hiroki Sumi在文献[3]中讨论了当G是有理半群的情形,得到了跟古典Fatou-Julia理论中相似的关于有理半群的斜积的Fatou集和Julia集的一些基本性质,但是并没有给出一个完整的证明.称一个集合M在某个映射ɡ下是完全不变的,指的是z∈M当且仅当ɡ(z)∈M.
TheoremAG=〈f1,f2,…,fm〉是一个有限生成有理半群,则







仿照Sumi的证明,不加证明给出下列结果.
定理11)G是一个由一族有限个超越整函数{f1,f2,…,fm}生成的半群.令Gn={ɡ∈G︱ɡ =…fω n∘ …∘fω 1}, 其中n∈N,ωj∈{1,2,…,m},j=1,2,…,n,…,则有J(Gn) = (fω n∘ …∘fω 1)-1(J(G));

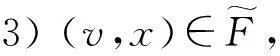
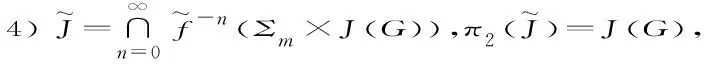
下面,给出本文的主要结果.
定理2令S={(ω,x)∈C|存在x的一个开邻域U和ω的一个开邻域V,使得对于每个α∈V,函数族{fα n∘ …∘fα 1} 在U内正规,n∈N},则有
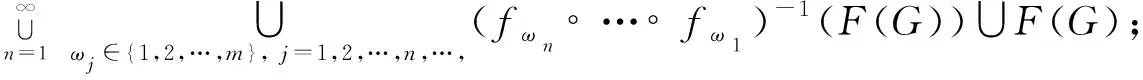
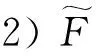
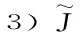

证明1)若x∈F(G),则存在x的一个邻域V,G在V内正规.任取一个ω∈Σm,都可以找到一个(ω,x)的一个邻域(Σm,V),使得对于任意的v∈Σm,函数族(fvn∘ …∘fv1)在V内正规,即(ω,x)∈S,则存在S中的一元(ω,x),使得π2(ω,x)=x,从而x∈π2(s).
假定x∈(fω n∘ …∘fω 1)-1(F(G)),其中n∈N,ωj∈{1,2,…,m},j=1,2,…,n.因为F(G)是开集,所以可以取x的一个足够小的邻域V,使得fω n∘ …∘fω 1(V)⊂F(G).那么,取ω的一个邻域为Un={α∈Σm|
αj=ωj,j=1,2,…,n}以及x的一个邻域为V.则(Un,V)为(ω,x)的一个邻域,且对于任意的α∈Un,函数族{…fα n∘ …∘fα 1} 在V内正规.这是因为函数族{ …fα n∘ …∘fα 1} 在V内正规等价于函数族{ …∘fα n + 2∘fα n + 1} 在fω n∘ …∘fω 1(V)内正规,由fω n∘ …∘fω 1(V)⊂F(G)可知这是显然的.所以有(ω,x)∈S且π2(ω,x)=x,从而x∈π2(s).
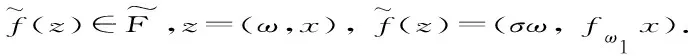

从而有

(1)
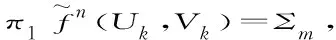

参考文献:
[1] HINKKANEN A,MARTIN G J.The dynamics of semigroups of rational function I[J].Proc.London Math.Soc.,1996,73(3):358-384.
[2] HINKKANEN A,MARTIN G J.Julia sets of rational semigroup[J].Math.Z.,1996,222:161-169.
[3] SUMI H.Skew product maps related to finitely generated rational semigroups[J].Nonlinearity, 2000,13:995-1019.
[4] POON K K. Fatou-Julia theory of transcendental semigroups[J].Bull.Austral.Math.Soc.,1998 ,58:403-410.
[5] 黄志刚.He dynamics of semigroups of transcendental meromorphic functions[J].Tsinghua Science and Technology,2004,9(4):472-474.
