Cu掺杂MgF2晶体的电子结构及光学特性

张治宇 韩培德,* 张彩丽 张 雪 孙向雷 李玉平

(1太原理工大学材料科学与工程学院,太原030024;

2太原理工大学新材料界面科学与工程教育部重点实验室,太原030024)

Cu掺杂MgF2晶体的电子结构及光学特性

张治宇1,2韩培德1,2,*张彩丽1,2张 雪1,2孙向雷1,2李玉平1,*

(1太原理工大学材料科学与工程学院,太原030024;

2太原理工大学新材料界面科学与工程教育部重点实验室,太原030024)

基于密度泛函理论(DFT)的第一性原理平面波超软赝势方法,计算了纯的MgF2晶体和掺杂不同原子分数(2.08%,4.16%,6.24%)Cu的MgF2晶体结构、电学性质以及光学性质.结果表明:Cu的掺入导致MgF2晶体禁带宽度逐渐变窄,并且Cu掺杂使得MgF2晶体折射率和吸收峰增加,特别是在4 eV附近区域出现了新吸收峰.同时也给出了引起体系性质变化的物理机制,Cu掺杂MgF2晶体在光电化学方面有着潜在的应用价值.

密度泛函理论;电子结构;光学特性;Cu;掺杂;MgF2

1 引言

MgF2具有折射率低(n=1.38)、能隙宽(Eg=10.08 eV)、可见及近红外波段吸收率低、热稳定性好和激光损伤阈值高等优异性能,成为光学透镜、激光元件、集成光学和光纤通讯等领域的重要光学镀膜材料,1-3近年来为了开发其优异性能,MgF2的调制掺杂成为近期的研究热点.如掺钴氟化镁(Co:MgF2)可以制作成激光器,且是目前调谐范围最宽的固体可调谐激光器;4Ni掺杂MgF2将有可能在稀磁半导体掺杂中扮演重要角色;5三价稀土元素(Sm、Eu、Yb)掺杂MgF2后可以构成固体发光中心;6Cu、Cr等与MgF2复合将改善其非线性光学特性以及吸收性能,有可能在光电催化等领域具有广泛应用前景;7-9同时MgF2与金属构成的非常规催化载体也可以有效阻止氟氯化碳(CFC)的液态脱氯作用,使催化过程的选择性得到更好控制.10,11

已有实验研究表明,由纳米金属微粒(Ni、Mn、Ag、Au、Cu、Cr)镶嵌于MgF2基体中所构成的纳米薄膜,12-15由于量子尺寸效应会引起独特的光电特性,表现在等离子体共振峰附近有很强的三级非线性光学效应、选择性强光吸收、巨电导、低电阻温度系数等特性方面的变化,尤其Cu:MgF2表现出了优异的非线性光学特性,因而吸引了人们广泛的关注.由于金属与MgF2薄膜界面间不可避免会产生元素间的相互作用,这可能会影响其微观结构及相关性能,尤其掺杂后MgF2的晶体结构及光学性质的研究还有待进一步深入,而这些研究的开展对于实验研究具有局限性,原子层次的计算模拟就显得尤为重要.

目前已有文献报道了各种元素(Co、Ni、O)掺杂MgF2的研究,如张计划等16对Co掺杂MgF2的结构和电子特性进行了研究,揭示了Co:MgF2体系由半导体-金属性转变的微观机理.Brik等17进行了Ni掺杂LiGa5O8,MgF2和AgCl的理论计算,用完整的能阶图分析了激发态Ni2+离子的吸收系数.李宗宝等18应用第一性原理的方法预测了O掺杂MgF2后体系晶体结构和光学性质变化的微观物理机制.但目前Cu:MgF2实验所表现出的非线性光学特性,对晶体结构、电学特性以及光学性质的物理机制的理论研究却鲜见报道.

本文利用第一性原理平面波超软赝势方法,将对比分析纯的MgF2和Cu掺杂MgF2晶体的几何结构、电子能带结构及其光学性质,探索禁带宽度、折射率和吸收系数随Cu掺杂量的变化规律和特征,所得结果对Cu掺杂MgF2的制备以及应用领域的开发将具有指导作用.

2 理论模型及计算方法

2.1 理论模型

MgF2是四方红宝石结构,空间群为P42/mn,晶格常数为a=b=0.4623 nm,c=0.3052 nm,α=β=γ=90°.19本文在计算中采用2×2×2的超晶胞作为完整晶体的计算单元,该超晶胞由8个MgF2单胞组成,总原子数为48个,结构式为Mg16F32,将其中的Mg原子用Cu原子代替作为掺杂Cu的MgF2晶体的计算单元,掺杂后的超晶胞组成为CuxMg16-xF32(x=1,2,3),x为Cu原子的掺杂个数.在超晶胞中我们对三种掺杂量Cu原子的占位进行了分析和结构优化,以确定不同掺杂量Cu原子的最佳占位.本文将分析三种Cu掺杂原子分数(2.08%、4.16%、6.24%)的CuxMg16-xF32三元化合物结构,MgF2超晶胞以及三个Cu原子掺杂的MgF2超晶胞结构模型如图1所示.

2.2 计算方法

本文采用基于第一性原理计算的密度泛函理论,结合平面波赝势方法的Castep(Cambridge serial total energy package)软件包.20-22在计算中,采用周期性边界条件,用局域密度近似(LDA)23,24的CA-PZ来处理电子间的交互关联能,选取Mg、F、Cu各原子的价电子组态为Mg 3s2、F 2s22p5、Cu 3d104s1.对三种元素均采用平面波超软赝势,平面波的截断能Ecut= 310 eV,第一布里渊区按2×2×3进行分割.结构优化的收敛条件为每个原子的能量变化在2.0×10-5eV以内;原子最大受力不超过0.5 eV·nm-1;最大压力不超过0.1 GPa;最大位移不超过0.0002 nm.获得优化后的晶胞结构再进一步计算电子结构等性质.根据获得的电子能带结构,研究其光学性质.

3 结果与讨论

3.1 Mg16F32超晶胞的晶体结构

图1 Mg16F32(a)和Cu3Mg13F32(b)超晶胞Fig.1 Mg16F32(a)and Cu3Mg13F32(b)supercells

Ramesh Babu等23用广义梯度近似(GGA)和局域密度近似(LDA)等方法对MgF2的几何结构进行了优化,发现用LDA方法优化的晶格常数与实验值更符合,计算结果为a=b=0.4603 nm,c=0.3037 nm, c/a=0.660.所以本文也用LDA方法对Mg16F32超晶胞进行优化,计算得到完整的MgF2晶格常数为a= b=0.4642 nm,c=0.3081 nm,c/a=0.664,而实验值为a=b=0.4625 nm,c=0.3052 nm,c/a=0.660,24二者非常接近,误差低于1%,并且计算值与文献值非常接近,说明所用的理论计算参数可靠.

表1 MgF2与CuxMg16-xF32的晶格常数及体系总能量(Etot)Table 1 Lattice constants and system total energy(Etot)of MgF2and Cu-doped MgF2

3.2 CuxMg16-xF32超晶胞的晶体结构及电子特性

3.2.1 CuxMg16-xF32(x=0,1,2,3)晶格常数

通过优化计算,我们分别得到了不同含量Cu掺杂下的CuxMg16-xF32(x=1,2,3)的晶格常数如表1所示.可以看出Cu掺杂后MgF2的晶格参数略有变化,这是由于Cu2+的离子半径为0.072 nm,Mg2+的离子半径为0.066 nm,25二者略有差异,所以Cu的掺入使a、b略有减小,c略有增加,体积几乎没有变化.表1还示出了不同掺杂浓度时,结构优化后的Cu:MgF2键长和键角,当x=1时,Cu―F键长相对于未掺杂结构中的Mg―F键长有所减小,而Cu―F(1)键长相对于原Mg―F(1)键长有所增加,但是Cu与它最近邻、次近邻的F原子的键角∠FCuF(1)仍为90°,这是由于Cu的掺入并没有改变原结构中各原子的相对位置,因而可维持体系的相对平衡,保持键角不变.当x=2时,Cu―F键长相对于原结构中的Mg―F键长有所减小,而Cu―F(1)键长相对于原Mg―F(1)键长有所增加,且Cu与它最近邻、次近邻的F原子的键角∠FCuF(1)为89.948°.当x=3时,Cu―F键长相对于原结构中的Mg―F键长有所减小,Cu―F(1)键长相对于原Mg―F(1)键长也有所减小,且Cu与它最近邻、次近邻的F原子的键角∠FCuF(1)仍为90°.结果表明现有掺入量的Cu不会引起整个体系中原子相互位置以及其晶体结构的变化.从表1中体系能量来看,Cu掺入后随着Cu含量的增加体系的总能量略有下降,但是由于单个Cu原子的能量要低于单个Mg原子的能量,所以单分析总能量是没有意义的.

3.2.2 CuxMg16-xF32(x=0,1,2,3)晶体结构的稳定性

晶体的结构稳定性与其结合能密切相关.晶体的结合能是自由原子结合为晶体所释放的能量,即晶体分解成单个原子时外界所做的功.结合能越小,则形成的晶体越稳定.

结合能计算公式为:

式中,Etot为超晶胞的总能量,和分别为孤立原子A、B和C的能量,NA、NB和NC分别为单胞中A、B和C的数量,在本文中A、B、C分别对应的是Mg、F、Cu,NA=16-x,NB=32,NC=x(x=1,2,3).结合能越小表明晶体结构越稳定.对理想结构的Mg16F32和CuxMg16-xF32超晶胞进行优化,得出优化后晶胞的总能量Etot,然后计算每个,为结合能.

3.2.3 CuxMg16-xF32(x=0,1)的能带与态密度

3.2.3.1 Mg16F32的能带与态密度

图2 CuxMg16-xF32(x=0,1,2,3)超晶胞结合能随Cu掺杂原子分数(αcu)的变化曲线Fig.2 Change curve of the binding energy of CuxMg16-xF32(x=0,1,2,3)supercell combined with the atomic fraction(αcu)of the Cu impuritied

利用以上计算获得的Mg16F32优化结构,计算了Mg16F32的能带结构、总态密度以及分波态密度,如图3(a,b)所示.结果表明本文计算的带隙值Eg为 6.67 eV,与其他基于DFT的计算值23,24基本一致,但是与实验值(10.08 eV)16相比明显偏小,这是因为用基于DFT的GGA与LDA都存在Eg计算值偏低的普遍性问题,计算得到的固体能带普遍偏小,对于MgF2晶体来说,主要是低估了Mg 3s态电子,结果使导带能量偏低,带隙变窄.但是其相对值的比较是准确的,而不会影响文中对比分析纯MgF2和Cu掺杂MgF2电子结构的结果.由图3(a,b)可知,-37 eV附近的价带区主要是Mg 2p态电子构成的;-20 eV附近的价带区主要是F 2s态电子构成的,由于这两个价带与费米面附近的价带相互作用较弱,我们将不做讨论;-4-0 eV附近的价带主要是F 2p态电子构成的,6.67-18.09 eV附近的导带主要是Mg 2p 3s态电子构成的.价带顶主要是F 2p态电子的贡献,导带底主要是Mg 3s态电子的贡献.的价带展宽而导带底向低能方向移动,导致掺杂后带隙为4.24 eV,明显小于Mg16F32超晶胞的6.67 eV,该结果与Co、Ni掺杂MgF2所起的作用一致.5,16由图4(a,b)可知,-39.5 eV附近的价带区主要是Mg 2p态电子构成的,-22.5 eV附近的价带区主要是F 2s态电子构成的,费米面附近的价带分为-6.5--2.5 eV的下价带、-2.5-0 eV的上价带区.从图4(b)可以看出,费米面附近的下价带区主要是由F 2p态电子和Cu 3d态电子构成的,而上价带区主要由Cu 3d态电子构成,4.24-15.6 eV的导带主要由Mg 2p3s和Cu 3p4s态电子共同构成.价带顶主要是Cu 3d态电子的贡献,导带底则主要是s态电子的贡献,以上现象说明由于Cu的掺入使材料发生了半金属性的转变,该现象与Ni掺杂MgF2结果5类似.

图3 Mg16F32的能带结构(a)和Mg16F32的分波态密度图(b)Fig.3 Band structures of Mg16F32(a)and partial density of states of Mg16F32(b)

图4 Cu1Mg15F32的能带结构(a)和Cu1Mg15F32的分波态密度图(b)Fig.4 Band structures of Cu1Mg15F32(a)and partial density of states of Cu1Mg15F32(b)

3.2.3.2 Cu1Mg15F32的能带与态密度

3.2.3.3 Cu掺杂后体系禁带宽度变窄及费米面附近价带展宽的机理

为了深入讨论Cu掺杂对MgF2带隙结构产生的影响,下面将以x=1为例进行讨论.图4(a,b)给出了Cu1Mg15F32超晶胞的能带结构及态密度图,对比图4 (a)和图3(a)可知,Cu掺杂的MgF2晶体费米面附近

图5给出了随掺杂量x的变化,Mg 3s和Cu 4s在导带底的分波态密度变化,随x的增加,Mg 3s和Cu 4s态电子都向低能方向移动,这是因为掺杂Cu以后Cu 4s态电子对导带有贡献.在纯净的MgF2中, Mg 3s态电子与F 2p态电子作用形成类s的反键和类p的成键,形成带隙.掺入Cu以后,Cu 4s态电子比Mg 3s态电子能量更低,Cu 4s态电子与F 2p态电子形成类s的反键,具有比Mg 3s态电子与F 2p态电子作用形成的反键更低的能量,从而使导带向低能方向移动,导带随着x的增加而下降.

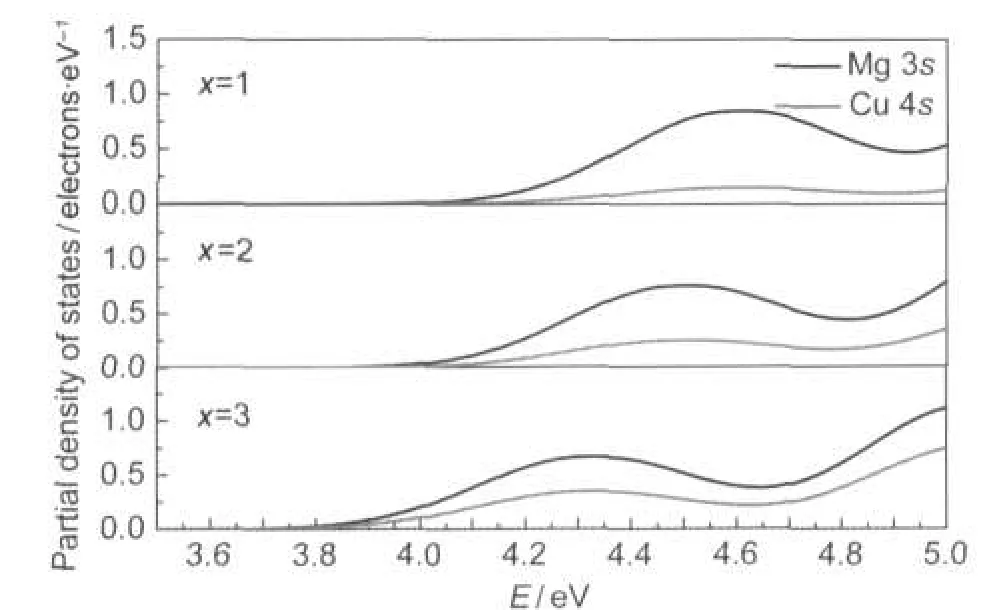
图5 CuxMg16-xF32(x=1,2,3)体系Mg 3s和Cu 4s在导带底的分波态密度图Fig.5 Partial density of states at bottom of CuxMg16-xF32 (x=1,2,3)conduction bands

Cu掺杂后费米面附近的价带展宽但价带顶变化不大,在F 2p态电子与Cu 3d态电子共同构成下价带,表明是Cu 3d态电子和F 2p态电子形成类p的成键,比Mg 3s态电子与F 2p态电子作用形成类p的成键具有更低的能量,使下价带向低能方向移动,剩余的Cu 3d态电子构成上价带,从而使费米面附近的能带展宽.

3.2.4 CuxMg16-xF32(x=0,1)的电荷密度分布

为了直观地分析掺杂机理,了解超晶胞中各原子间的成键情况、电荷分布,图6显示了未掺杂和掺杂情况下超晶胞的电荷密度分布,由图可见,未掺杂和掺杂Cu后原子间相互作用差异较大,体系中电荷发生了重新分配.在未掺杂的MgF2体系中,Mg和F之间形成离子键的特征,而在掺杂体系中,可以看到Cu与邻近的F产生相互作用的电子分布特征,Cu与F成键的离子性要大于Mg与F成键的离子性.从表1中也可以看到Cu―F键长较掺杂前的Mg―F键长短,即Cu―F成键强度增强.这是由于Cu的电负性1.90,大于Mg的电负性1.20.所以Cu原子和F原子成键离子性强于Mg原子和F原子成键的离子型.

3.3 光学性能

在线性响应范围内,固体的宏观光学响应函数通常可用复折射率(式(2))来描述.

图6 Mg16F32(110)(a)和Cu1Mg15F32(110)(b)晶面的电荷密度分布(Fcharge)Fig.6 Charge density distribution(Fcharge)of Mg16F32(110)(a)and Cu1Mg15F32(110)(b)crystal surfaces The contour lines are drawn from-10 to 10 electrons·nm-2.

根据直接跃迁概率定义和克拉默斯-克勒尼希(Kramers-Kronig)色散关系可以推导出晶体折射系数N(ω)、吸收系数η等,26相关公式如下:

式中ε1、ε2分别为介电函数实部和虚部,m为自由电子质量,e为电子电量,ω为入射光子频率,C和V分别表示导带和价带,K为倒格矢,EC(K)和EV(K)分别为导带和价带上的本征能级.BZ为第一布里渊区, |e·MCV(K)|2为动量跃迁矩阵元,ω为角频率,λ0为光在真空中的波长.这些基本关系反映了能级间电子跃迁产生光谱的发光机理,是分析晶体能带结构和光学性质的理论依据.

3.3.1 CuxMg16-xF32(x=0,1,2,3)的折射率

图7给出了未掺杂MgF2折射率实验值、27计算值和Cu掺杂MgF2折射率计算值与波长的关系.从图7可以看出,MgF2折射率的实验曲线和计算曲线拟合度非常接近,说明计算结果可靠,准确度高.对比纯MgF2和Cu掺杂的MgF2可以看出,Cu掺杂后体系实部明显高于未掺杂的MgF2;虚部在300-500 nm处略有增加,但在500 nm以后影响非常小,几乎接近于0,总体看来Cu掺杂后使整个体系折射率实部增加而虚部影响不大.

图7 MgF2以及Cu掺杂MgF2折射率的实验值27和计算值Fig.7 Experimental27and calculatied refractive indexes of MgF2and Cu-doped MgF2n is real part of refractive index;k is imaginary part of

图8 Cu掺杂MgF2的吸收系数(η)Fig.8 Absorption coefficient(η)of Cu-doped MgF2

3.3.2 理想的MgF2晶体以及三种不同掺杂量情况下的吸收函数的比较

图8为不同掺杂量情况下CuxMg16-xF32沿(100)极化方向上的吸收系数计算值.

未掺杂的MgF2吸收系数与文献16计算结果一致(文献中因为存在剪刀因子的缘故,整体向高频方向移动了3.11 eV),说明计算参数可靠.对比纯MgF2和Cu掺杂的MgF2可以看出,Cu掺杂后体系吸收率明显增加并在低频区域即2-6 eV范围内出现了新的吸收峰.这可以用态密度图3(b)和图4(b)来解释,未掺杂的情况下,F 2p态电子在费米面附近存在峰值;而掺杂状态下,Cu 3d态电子在费米面存在峰值,且费米面附近价带展宽.因此,杂质原子的掺入在费米面附近提供了大量的导电电子,改变了电子在带间的跃迁,使得掺杂后4 eV区域吸收系数增大.对比图3(b)和图4(b)发现,掺杂后禁带宽度明显变窄,这是导致掺杂后新的吸收峰出现的本质原因.对比不同掺杂浓度的吸收系数可以看出并不是掺杂浓度越高新出现的吸收峰越强,可能存在一个极限值,当掺杂浓度超过这个极限值后,吸收系数下降.这一特性表明Cu掺杂对MgF2的吸收系数、折射率等有重要的调节作用,在光学器件及光电催化方面有很好的应用前景.

4 结论

采用基于密度泛函理论的局域密度近似(LDA)的超软赝势能带计算方法研究了MgF2和Cu:MgF2晶体的几何结构、电学性质以及光学性质.计算结果表明,Cu的掺入使得掺杂体系的禁带宽度变窄,且使费米面附近能带展宽,说明掺入Cu对体系的能带结构特别是费米面的能带结构有重要的调节作用;Cu掺杂可以使体系的折射率和吸收系数增加,且在4 eV附近区域出现了新的吸收峰.表明掺杂可以调制材料的电子结构,改善材料的光学性质.所得的结果对Cu掺杂MgF2体系在光电催化领域的应用具有一定的指导作用.

(1) Nofar,M.;Madaah Hosseini,H.R.;Shivaee,H.A.Infrared Phys.Technol.2008,51,546.

(2) Perales,F.;Herrero,J.M.;Jaque,D.;De las Heras,C.Opt. Mater.2007,29,783.

(3)Yu,H.;Qi,H.J.;Cui,Y.;Shen,Y.M.;Shao,J.D.;Fan,Z.X. Appl.Surf.Sci.2007,253,6113.

(4) Di Lieto,A.Optics and Lasers in Engineering 2003,39,309.

(5)Brika,M.G.;Avramb,C.N.;Avram,N.M.J.Phys.Chem. Solids 2008,69,1796.

(6) Pena,A.;Camy,P.;Benayad,A.;Doualan,J.L.;Maurel,C.; Olivier,M.;Nazabal,V.;Moncorgé,R.Opt.Mater.2011,33, 1616.

(7) Wojciechowska,M.;Haber,J.;Łomnicki,S.;Stoch,J.J.Mol. Catal.A-Chem.1999,141,155.

(8) Sun,Z.Q.;Xiao,L.;Cao,L.;Song,X.P.;Sun,D.M.Chin.Opt. Lett.2009,7,10.

(9)Wojciechowska,M.;Malczewska,A.;Czajka,B.;Zieli´nski, M.;Goslar,J.Appl.Catal.A 2002,237,63.

(10)Wojciechowska,M.;Przystajko,W.;Zieliʹnski,M.Catalysis Today 2007,119,338.

(11) Tomska-Foralewska,I.;Zieliʹnski,M.;Pietrowski,M.; Przystajko,W.;Wojciechowska,M.Catalysis Today 2010,12, 16.

(12) Secu,M.;Secu,C.E.;Jipa,S.;Zaharescu,T.;Cutrubinis,M. Radiat.Meas.2008,43,383.

(13)Sun,Z.Q.;Sun,D.M.;Ruan,T.N.Vacuum 2003,68,155.

(14) Sun,Z.Q.;Cai,Q.;Song,X.P.Thin Solid Films 2008,516, 2280.

(15) Sun,Z.Q.;He,Y.P.;Song,X.P.;Sun,D.M.Acta Phys.Sin. 2003,52,6.[孙兆奇,何玉平,宋学萍,孙大明.物理学报, 2003,52,6.]

(16) Zhang,J.H.;Ding,J.W.;Lu,Z.H.Acta Phys.Sin.2009,58, 1901.[张计划,丁建文,卢章辉.物理学报,2009,58,1901.]

(17) Brik,M.G.;Sildos,I.;Kiisk,V.Physica B 2010,405,2450.

(18) Li,Z.B.;Zhu,Y.;Yao,K.L.J.Mol.Sci.2011,27,4.[李宗宝,祝 娅,姚凯伦.分子科学学报,2011,27,4.]

(19)Fang,C.M.;Ramanujachary,K.V.;Hintzen,H.T.;de With,G. J.Alloy.Compd.2003,351,72.

(20) Zhukovskii,Y.F.;Kotomin,E.A.;Fuks,D.;Dorfman,S.Surf. Sci.2004,566,122.

(21) Chahed,A.;Benhelal,O.;Laksari,S.;Abbar,B.;Bouhafs,B.; Amrane,N.Physica B 2005,367,142.

(22)Zhang,F.C.;Zhang,W.H.;Dong,J.T.;Zhang,Z.Y.Acta Phys.-Chim.Sin.2011,27(10),2320.[张富春,张威虎,董军堂,张志勇.物理化学学报,2011,27(10),2320.]

(23) Ramesh Babu,K.;Lingam,C.B.;Auluck,S.;Tewari,S.P.; Vaitheeswaran,G.J.Solid State Chem.2010,10,1016.

(24) Vassilyeva,A.F.;Eglitis,R.I.;Kotomin,E.A.;Dauletbekov,A. K.Physica B 2010,405,2125.

(25) Dang,S.H.;Li,C.X.;Han,P.D.Acta Phys.Sin.2009,58, 4137.[党随虎,李春霞,韩培德.物理学报,2009,58,4137.]

(26) Bi,Y.J.;Guo,Z.Y.;Sun,H.Q.;Lin,Z.;Dong,Y.C.Acta Phys. Sin.2008,57,7800.[毕艳军,郭志友,孙慧卿,林 竹,董玉成.物理学报,2008,57,7800.]

(27) http://refractiveindex.info/?group=CRYSTALS&material=MgF2

July 20,2011;Revised:November 16,2011;Published on Web:December 6,2011.

ZHANG Zhi-Yu1,2HAN Pei-De1,2,*ZHANG Cai-Li1,2ZHANG Xue1,2SUN Xiang-Lei1,2LI Yu-Ping1,*

(1College of Materials Science and Engineering,Taiyuan University of Technology,Taiyuan 030024,P.R.China;2Key Laboratory of Interface Science and Engineering in Advanced Materials,Ministry of Education, Taiyuan University of Technology,Taiyuan 030024,P.R.China)

Based on the density functional pseudopotential method,the geometries,electronic structures, and optical properties of MgF2with different atomic fractions of Cu doping(2.08%,4.16%,and 6.24%)are compared in detail.Cu substitution of the Mg sites induces an effective reduction of the band gap of MgF2; and the band gap is continuously reduced with increasing Cu doping level.Also,the calculations show that the refractive index and absorption increase with increasing Cu doping.More importantly,an absorption around 4 eV is found.The mechanisms of this transition in the doped and undoped materials are discussed.The Cu doped MgF2system could be a potential candidate for photoelectrochemical applications.

Density functional theory;Electronic structure;Optical property;Cu;Dope;MgF2

10.3866/PKU.WHXB201112061

*Corresponding authors.HAN Pei-De,Email:hanpeide@tyut.edu.cn;hanpeide@126.com;Tel:+86-351-6018843.

LI Yu-Ping,Email:liyuping@tyut.edu.cn.

The project was supported by the National Natural Science Foundation of China(50874079,51002102)and Taiyuan Science and Technology Project,China(100115105).

国家自然科学基金(50874079,51002102)和太原市科技项目(100115105)资助

O641;O649

Electronic Structures and Optical Properties of Cu:MgF2Crystal