《电磁学》中静电类问题的可视化仿真实验设计

赵小龙 王玉平 鲍丽红

（天水师范学院物信学院，甘肃 天水 741001）

《电磁学》中静电类问题的可视化仿真实验设计

赵小龙 王玉平 鲍丽红

（天水师范学院物信学院，甘肃 天水 741001）

《电磁学》中基本概念、基本规律理论性强、场图复杂.针对离散点电荷系在空间产生的场分布、静电场中导体的静电感应现象、静电场中电介质的极化现象等典型静电类电磁问题，利用Matlab中的偏微分方程工具箱（PDEtool）、数学物理方程进行可视化仿真实验设计.仿真结果中电场线、等势线的分布很好地体现出典型电磁现象及相关物理性质，有助于信息技术条件下的教学方法改革.

电磁学；静电类问题；偏微分方程；可视化仿真

1 引言

《电磁学》［1］是物理类、电子信息类专业的基础课程，课程讲授应该使学生全面系统地掌握电磁运动的基本现象、基本概念和基本规律，使其具有一定分析和解决电磁学问题的能力.由于课程理论性强、概念抽象、推导繁多、场图复杂，要求学生具有较强的抽象思维能力和空间想象力.目前，理论讲授的现状是多数学生对基本概念掌握较好，而针对物理问题运用数学方法求解问题的能力偏弱.而配套的《电磁学实验》［2］中除静电场的描绘、霍尔效应等外，多数实验仍是电路基础、电工学中的基础电学实验.可视化仿真实验设计能够形象地、动态地展示电磁理论的基本原理、模拟出电磁场中的物理量，同时能以图形化的方式显示其分布及其计算结果，得到富有感染力的三维图形及计算结果，有助于增强学生的学习兴趣、巩固和掌握所学理论，改善教学效果［3～5］.

2 静电场

静电场是电磁学教科书中最基础、最重要的章节，内容涉及库仑定律、电场强度、电势、静电场中的导体和电介质、唯一性定理、边界条件、电场能量等，其关于静电场中的物理量、静电场性质的表述在结构上与稳恒磁场的内容遥相呼应.因此，准确、清晰地掌握静电场的知识点对整个教材教学目的的实现具有重要作用.

静电场内容首先从基本的电现象出发，通过两个点电荷相互作用满足的基本实验定律——库仑定律，引出了电场的概念及描述电场的物理量——电场强度.为进一步揭示场的性质，通过电通量和电场力做功得到高斯定理和保守力场的结论，同时定义了描述场的另外一个物理量——电势.通过对处在静电场中的导体和电介质引出静电感应和介质极化，更是将静电问题一般化.唯一性定理和边界条件保证了对于任意的静电类问题都可以通过泊松方程进行求解.整个过程都是通过微积分以及微分方程的形式对问题一一进行分析、求解，并从解中探寻场的性质与特征.因此，数值分析求解方法应该是贯穿整个章节内容的基本手段.

2.1 叠加原理

叠加原理是教材中针对点电荷系、连续带电体等静电问题最基本的解决方法.无论是对电场强度矢量E，还是电势U，都可由点电荷在空间的E、U分布和叠加原理求解点电荷系、连续带电体在空间的场分布特征.具体计算公式如下

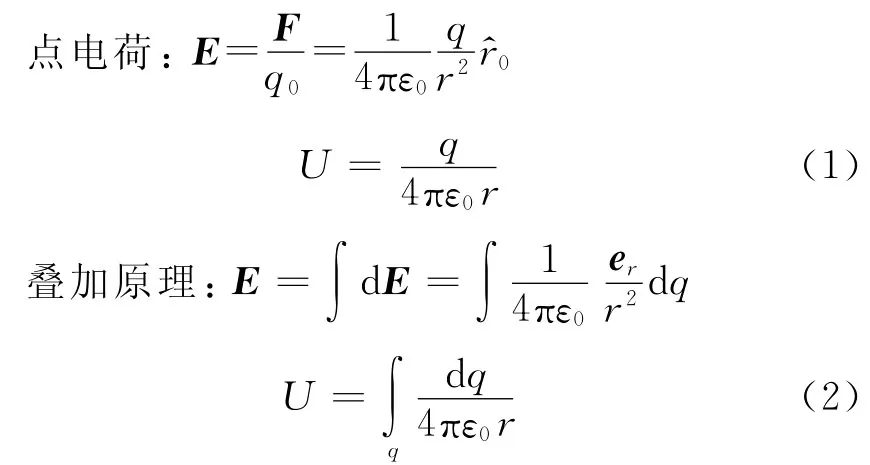
2.2 泊松方程

利用静电场中高斯定理的微分形式及关系式E＝－ΔU，则可得到泊松方程

式中，ρ为电荷分布体密度；ε是介质介电常数.泊松方程是一个二阶偏微分方程，其解需根据边界条件来确定.静电场中导体及介质的边界条件分别如下

导体边界：U（r）｜S＝ψ｜S

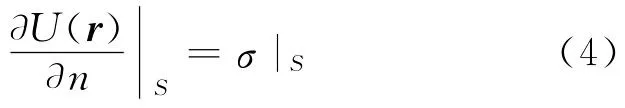
介质边界：U1（r）｜S＝U2（r）｜S

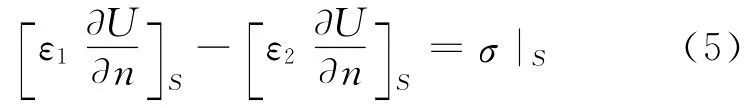
3 算例设计与仿真

带电体的静电场分布、静电场中介质的极化现象、静电场中导体的静电感应现象是静电场的重点内容，也是难点内容.本文以两点电荷构成的点电荷系——电偶极子、静电场中的介质球、静电场中的导体圆柱为研究对象，分别对场图的描绘进行可视化设计.

对于离散的点电荷系，叠加原理的应用可通过Matlab的编程指令及Streamline、Arrows等绘图命令画出电场线、等势线来表现静电场的物理图像，实现矢量场的可视化，这对比较和正确理解问题的结果是很重要的.而对于连续的带电体，泊松方程的应用主要是利用Matlab中求解二阶偏微分方程的有力工具——偏微分方程工具箱（PDEtool）.针对具有确定边界条件的静电类泊松方程，PDEtool能使用彩图、高度图、矢量场图等形式将结果可视化，让枯燥的公式伴以生动的图像，让深奥的内容有了鲜明的物理图像.

例1计算电偶极子的电场强度.

解如图1所示，利用叠加原理式（1）、式（2）计算离散点电荷系产生的电场强度和电势，电偶极子产生的电势为

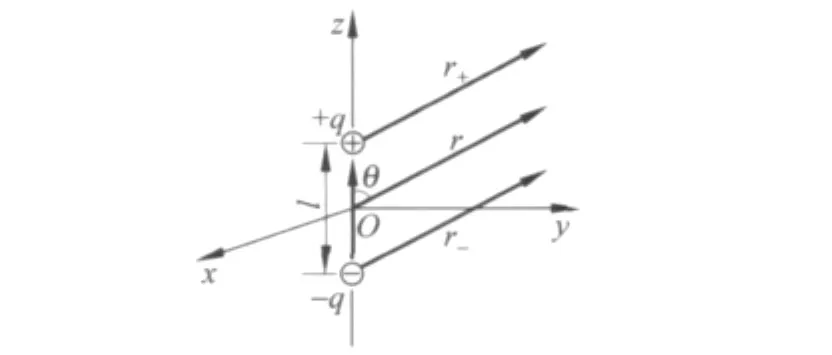
图1 电偶极子

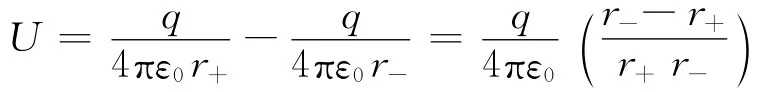
若场点距离远大于间距l，则可认为er＋∥er，er－∥er，那么解得

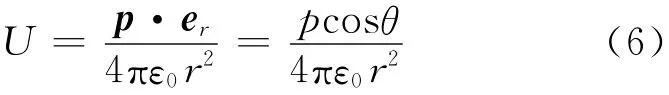
其中，p是电偶极子的电偶极矩.已知E＝－U，求得电偶极子的电场强度为

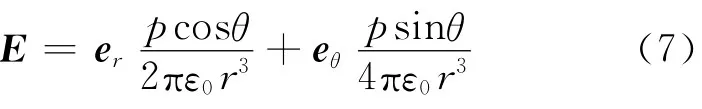
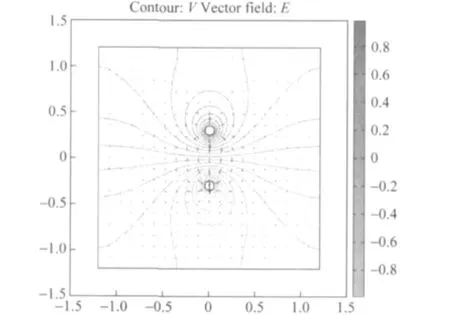
图2 电偶极子的电场线和等势线

例2设半径为a，介电常数为ε的介质球放在无限大的真空中，受到均匀电场E0的作用，如图3所示.试求介质球内外的电场强度.

图3 静电场中的介质球

解取球坐标系，令E0＝E0ez.显然，介质球内外的电势分布满足ρ＝0时的泊松方程（3）和介质边界的边界条件（5）.利用分离变量法求解的过程详见文献［6］，此处不再赘述.介质球内、外电势分别为

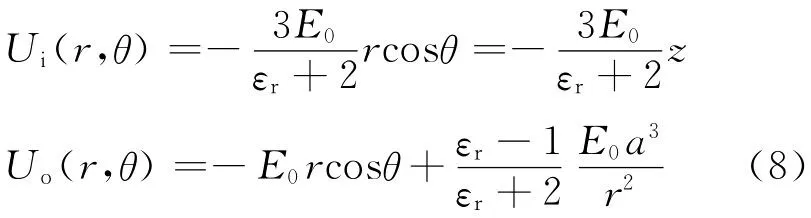
根据E＝－U，求得介质球内的电场为

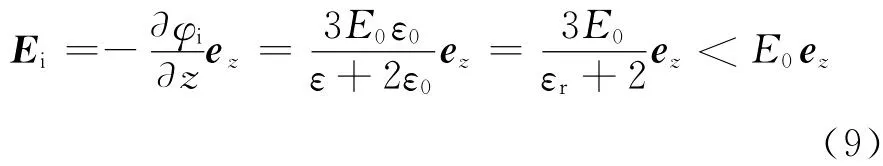
图4是利用PDEtool工具箱解得的介质球内外电场线和等势线分布图.从图中可以看出：介质球内静电场仍然为均匀电场，而且球内场强明显低于球外场强；介质球外较远区域静电场保持初始场的分布，而介质球表面附近区域场分布变化显著、等势线弯曲受介质表面极化现象影响显著.

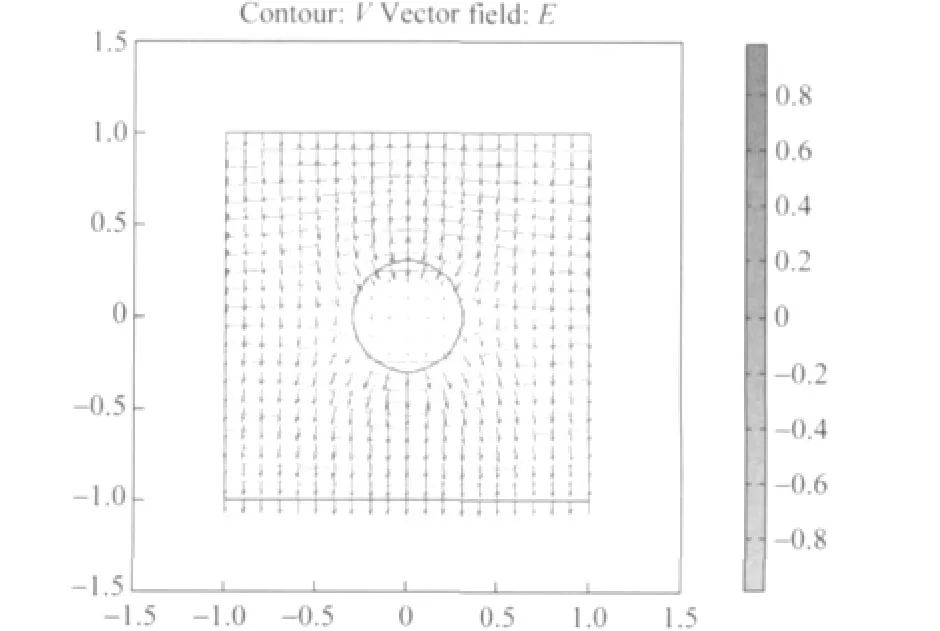
图4 介质球内外的电场线和等势线

例3设一根无限长的导体圆柱位于均匀静电场中，电场强度方向垂直于导体圆柱.试求导体圆柱外的电场强度.

解选取圆柱坐标系，令E0＝E0ex.当导体圆柱处于静电平衡时，圆柱内的电场强度为零、圆柱为等势体，圆柱表面电场强度切向分量为零，且柱外的电势分布函数与z无关.导体圆柱外的电势分布满足泊松方程（3）和导体边界的边界条件（4），圆柱外电势分布函数为

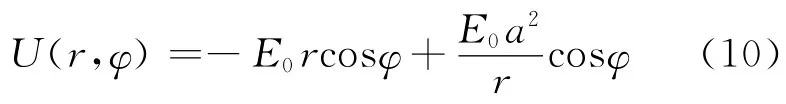
图5 静电场中的导体圆柱

圆柱外电场强度为

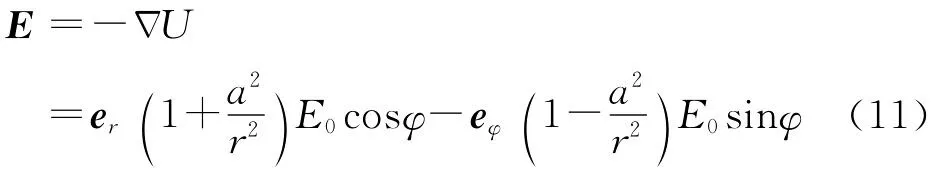
导体圆柱内外电场线、等势线分布如图6所示.从图6中可以看出：导体圆柱内无电场线分布，即电场强度为零；导体表面有部分电场线穿入，这可以帮助学生很好地理解电磁波在导体表面的趋肤效应和穿透深度的概念；导体圆柱外较远区域静电场保持初始场的分布，而导体圆柱上下表面附近区域场分布显著较强、等势线弯曲受导体表面静电感应现象影响显著.导体圆柱内外电场线、等势线的伪彩色分布图可以很好地帮助学生理解并掌握静电感应现象和静电平衡时静电场的性质和特点.

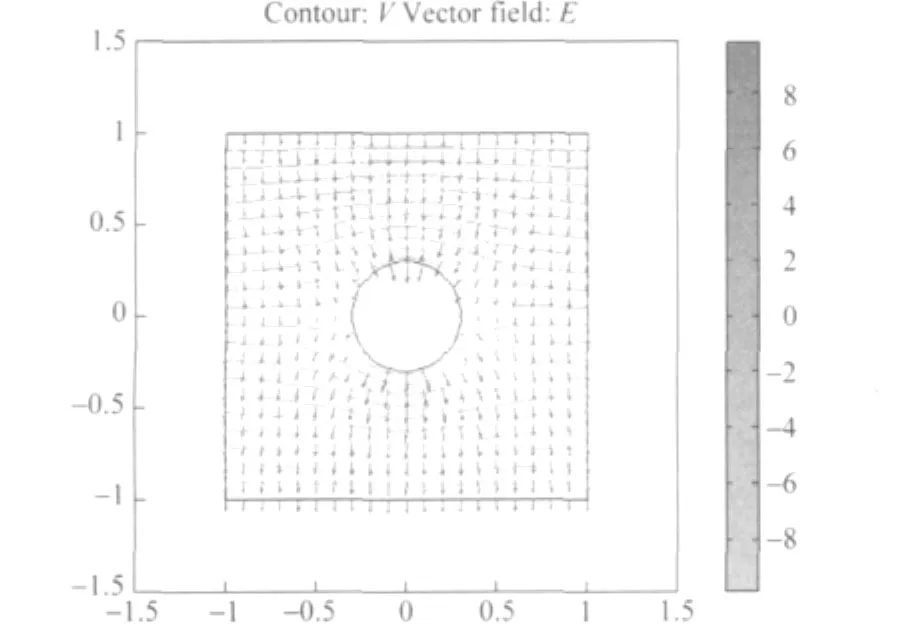
图6 导体圆柱内外的电场线和等势线

4 结论

《电磁学》课程中物理概念抽象、理论性强、场图复杂，借助于Matlab的可视化程序设计指令和PDEtool偏微分方程工具箱以及物理物理方程中的相关理论知识，静电类可视化仿真实验设计不仅有利于学生掌握理论知识、培养学生运用新技术、新方法的能力，而且有助于学生完成课程设计、毕业设计等教学任务.在整个实验设计过程中不仅能让学生知道结果，更要学会方法，让学生探索性地解决专业知识学习过程中所遇到的问题，以实现工程应用能力和创新能力的培养，对学生适应社会需求、提高自身的能力和素质具有重要的现实意义.

［1］ 赵凯华.电磁学［M］.2版.北京：高等教育出版社，2002

［2］ 杨述武.普通物理实验（二、电磁学部分）［M］.3版.北京：高等教育出版社，2000

［3］ 彭芳麟.数学物理方程的Matlab解法与可视化［M］.北京：清华大学出版社，2004：11

［4］ 熊万杰.Matlab用于大学物理教学［J］.物理通报，2004，（2）：16～19

［5］ 陈执平.本科电磁场教学中引入ANSYS的尝试［J］.大学物理，2010，29（7）：32～35，54

［6］ 杨儒贵.电磁场与电磁波［M］.北京：高等教育出版社，2007

VISUAL SIMULATION DESIGN ON ELECTROSTATIC PROBLEM IN ELECTROMAGNETISM

Zhao Xiaolong Wang Yuping Bao Lihong
（Institute of Materials，Tianshui Normal University，Tianshui，Gansu 741001）

Basic concepts and principles in Electromagnetism have abstract reasoning and complicated field－map.Typical electrostatic electromagnetic problems such as the electric field distribution of discrete point－charge group in the space，electrostatic induction phenomenon of conductor in electrostatic field，and polarization phenomenon of dielectric in electrostatic field，can be visually simulated by PDEtool in Matlab and Mathematical physics equations.The simulation results show that the electric field lines and equipotential lines describe well the electromagnetic phenomena and physical properties.The simulation design is beneficial to teaching reform by information technology.

electromagnetism；electrostatic problems；partial differential equation；visual simulation

2011－06－08）

项目资助国家自然科学基金（61002008），甘肃省教育厅项目（1008B－11），天水师范学院“青蓝”人才工程.

赵小龙（1976年出生），男，甘肃天水人，博士，副教授，电子学会高级会员.主要研究方向为电磁理论研究及教学.