斜面上颗粒物质冲击力的实验研究

赵 振 胡 林 余幼胜 王星云 庚振凯

（贵州大学理学院，贵州 贵阳 550025）

斜面上颗粒物质冲击力的实验研究

赵 振 胡 林 余幼胜 王星云 庚振凯

（贵州大学理学院，贵州 贵阳 550025）

通过实验研究了颗粒在斜面上的流动现象，考察了同一倾角下，颗粒流动产生的冲击力F与颗粒直径D和滑移距离L的关系，并给出了在垂直于颗粒流动方向的横截面上，饱和冲击力Fb的分布.

颗粒流；冲击力；颗粒直径；滑移距离；颗粒介质表面分布

1 引言

颗粒物质是指尺度大于1μm的大量固体颗粒的集合体，在日常生活及工业生产和交通运输中普遍存在［1］，比如煤、矿石、化肥等.颗粒在斜面上的流动是许多工业过程的重要组成部分，如颗粒在斜槽中的输运，在旋转机械中的粉碎、干燥，以及在料仓中的填充堆积等，都与其在斜面上的流动行为有着密切的关系.颗粒在斜面上的流动行为也广泛存在于自然界中，尤其是近些年来地球上频频发生的地震、雪崩、泥石流、滑坡等自然灾害，给人们的生命安全和经济财产造成了巨大的损失，在这些灾害过程中，颗粒流的冲击是造成破坏的主要因素.因此，研究颗粒流在斜面上的运动行为，有助于帮助人们认识这类冲击现象，增进人们对自然灾害的形成、演化和致灾机理的认识以及预报调控水平，具有重要的科学意义和现实意义.

进入21世纪以来，物理学界加强了对颗粒物质斜槽流的实验研究.很多研究人员通过不同的实验方法和研究手段，从多方面对颗粒物质在斜面上的流动开展研究.陈洪凯等人［2］通过建立泥石流冲击试验模型研究了沟谷泥石流冲击荷载的变化规律，并初步建立了泥石流中固液分相冲击力计算方法［3～5］；张洲波等人［6］则用示踪颗粒法测量了玻璃球在斜槽中流动时，不同条件下的速度分布和流层厚度；朱鸿琛等人［7］通过搭建三维沙漏实验模型，研究了颗粒流量与颗粒尺寸和漏斗开口及倾角之间的关系；刘传平等人［8］基于“拟流体”的思想，给出了在颗粒斜槽流实验中测量颗粒流本构关系的实验方法；Hungr和Morgenstem［9］以染色玻璃球为示踪颗粒，测量了沙子和聚苯乙烯颗粒在有机玻璃表面上流动的表面速度及流层厚度分布.基于室内物理模型试验和现场观测，颗粒流动属于非经典介质的流动，颗粒流问题看似简单，实际却十分复杂，尽管对于颗粒单体有较成熟的弹性力学和塑性力学理论，但是颗粒流整体上表现出来的行为却不能被现有的流体力学理论给予适当的描述和解释.虽然已有很多学者做了大量的研究，但我们在文献调研中发现关于颗粒物质在斜面上流动时产生冲击力的研究报道很少.本研究通过实验观测了颗粒在斜槽中流动时产生的冲击力，并根据实验结果分析讨论了颗粒流产生的冲击力F与颗粒尺寸D和滑移距离L的关系，得到了颗粒沿斜面流动达到稳定时，冲击力沿垂直于斜面中轴线两侧的横向分布规律.

2 实验装置及测量方法

实验装置如图1所示，主要由供料斗、堆料仓、玻璃斜面（两边有挡板）、探针（与传感器连接）、回收槽等组成.供料斗用于存储颗粒物质，堆料仓的作用用于消除供料斗中颗粒堆高度变化对颗粒流量的影响［5］.颗粒出口槽由光滑坚硬的铝板制成，出口尺寸为20.0mm×40.0mm，在出口处由抽插板控制颗粒流动的开始与停止.玻璃板斜坡长780.0mm，倾角θ为31°，底面及两边挡板均为光滑的玻璃板，玻璃板下面有回收槽以保证下滑的颗粒不会在斜面上滞留.实验时向供料斗和堆料仓中分别填入不同直径的密度均为ρ0＝2.5g/cm3的球形玻璃颗粒.颗粒在斜面上流动产生的冲击力由与称重传感器（量程0.3kg）相连的探针（宽度为d＝5.00mm）测得.为了消除偶然误差对实验结果造成的影响，每次实验在相同条件下重复三次.

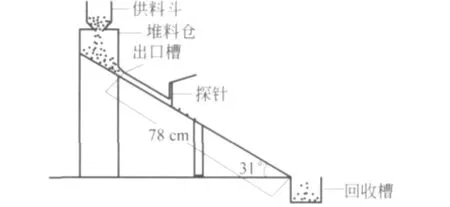
图1 实验装置图

3 结果与讨论

3.1 颗粒流产生的冲击力F与颗粒直径D 的关系

实验时，将探针置于距离堆料仓出口75.0mm处，向供料斗和堆料仓中依次填充直径分别为0.7、1.0、1.3、2.1、3.2、3.8mm 的颗粒.待颗粒堆积稳定后，抽开堆料仓出口插板，颗粒在重力作用下沿斜面滑动，当颗粒与探针发生碰撞时，即可测到不同尺寸的颗粒在相同滑移距离L处产生的冲击力F随时间t的变化关系，如图2所示.图2中曲线的上升沿表示，颗粒与探针碰撞时产生的冲击力F在极短时间内迅速从零达到饱和值Fb，随后保持一个稳定的饱和值；当颗粒直径D较小时，达到稳定流动时产生的饱和冲击力Fb曲线比较平稳，随着D的增大，Fb曲线出现不稳定的锯齿形脉动；下降沿表示，随着供料斗和堆料仓内颗粒的减少，斜面上颗粒的流量逐渐减小，F也逐渐下降直至减小到零.比较不同直径颗粒的冲击力发现，随着D的增大，饱和冲击力Fb增大.

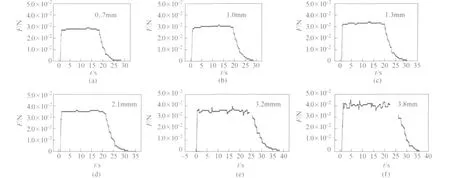
图2 不同尺寸的颗粒产生的冲力F随时间t的变化关系

由实验数据分析知，当颗粒直径D较小时，单个颗粒的动量P很小，颗粒直径D与探针宽度d的比值D/d也很小，因此颗粒与探针碰撞频率f较大，故宏观曲线表现出较平稳；随着D值增大，P和D/d逐渐增大，即冲击力正比于颗粒流动量（F∝P）.同时，颗粒尺寸增大，颗粒间隔增大，碰撞频率减小，表现为曲线的锯齿形波动（微扰被明显展示）.这种现象反映出颗粒流与连续介质流的区别.比较图2中颗粒直径为0.7mm和3.8mm时的F—t图可明显看出这种区别.

颗粒流动稳定时产生的饱和冲击力Fb与颗粒直径D的关系如图3所示，可见：随着粒径D增大，Fb增大.其中当D＜1.5mm时，Fb增长很快；当2.0mm＜D＜3.5mm时，Fb的增速较缓慢；当D＞3.5mm后，Fb又急剧增大.实验结果表明饱和冲击力Fb与颗粒尺寸的关系并非简单的线性关系，除了颗粒尺度因素以外，可能还有其他因素的影响，有待进一步研究.

图3 颗粒尺寸D与冲击力Fb的关系

3.2 颗粒流动时产生的冲击力F与滑移距离L的关系

实验时，向供料斗和堆料仓中加入直径为2.1mm的颗粒，分别将探针位置置于斜面上距离出口 80mm、100mm、120mm、140mm、160mm、180mm、200mm、240mm、280mm、320mm、360mm处（待测点位于出口的中轴线上），同一位置处重复实验3次，得到图4所示饱和冲击力Fb与滑移距离L的关系.曲线表明随着L的增大，Fb与L呈现出类似指数关系的减小趋势.其原因可作这样理解：沿出口槽中轴线方向颗粒的流速为vt，由于颗粒间的相互推挤，部分颗粒流动方向偏离轴向，因而，流动过程中同时产生一个垂直于中轴线方向的速度vn，于是，颗粒向下流动的过程中不断向两边发散，颗粒流密度ρ不断减小.同时，考虑到玻璃槽与颗粒之间的摩擦系数很小，因此，随着距离L的增大，中轴线上颗粒运动速度v增大，单个颗粒动量P也在增大，且颗粒流密度ρ的减小率大于速度增长率.鉴于以上因素，随着L的增大，颗粒流向中轴线两侧扩展，沿中轴线运动的颗粒数量减小，单位时间撞击在探针上的颗粒数量也逐渐减小，因此，探针测到的饱和冲击力Fb随L增大逐渐减小.即受颗粒流密度和动量的影响，冲击力Fb随距离L的变化呈指数减小趋势.

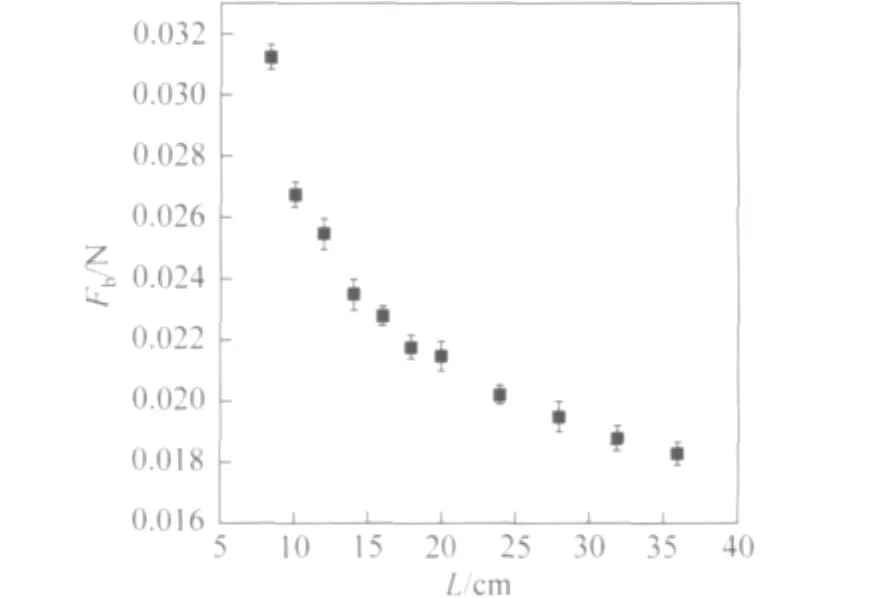
图4 饱和冲击力Fb与滑移距离L的关系

3.3 稳定冲击力F沿斜面横向的分布

向供料斗和堆料仓中分别加入直径为1.0、1.3、2.1、3.2mm的颗粒，待颗粒流动稳定后用步进电机对距离出口80.0mm的斜面进行横向扫描，测到冲击力沿斜面横向的分布，如图5所示：颗粒流的冲击力F以出口中轴为对称，向两侧均匀分布.中轴上冲力F的值最大，并由中轴向两侧逐渐减小.分析认为，大量颗粒在相互推挤和自身重力作用下从槽口快速流出后，虽然颗粒前后层间的压力分布权重有所不同，但是，对于大量同类球形颗粒而言，宏观上仍然服从统计的正态分布规律.这与鲍德松等人［10］认为的，随着通道宽度从宽变窄，颗粒流量在通道内的分布将从对称的马鞍型分布逐渐变成抛物线分布的结论吻合.

图5 颗粒流动稳定时产生的冲力F沿斜面横向的分布

4 结论

本实验研究表明，沿斜面下滑的全同颗粒流所产生的冲击力F的大小与颗粒直径D和滑移距离L有关.颗粒流动达到稳定时，在斜面上某一点产生的饱和冲击力Fb随着颗粒直径D的增大呈非线性增大；饱和冲击力Fb随着滑移距离L的增大呈指数衰减趋势；大量颗粒流产生的冲击力F以出口中轴线为轴对称分布，类似具有粘滞性的层流，沿流动中轴向两侧对称递减.根据对实验结果的分析我们认为，颗粒流在斜面横截面上的对称分布类似于连续流体的层流分布；流动过程中对某一截面所产生的冲击力与颗粒尺寸和运动距离有关，这是颗粒流与连续介质流所不同之处.因此，有必要深入研究这类新型的凝聚态物质的物理行为，从而正确理解和描述其物理性质及运动规律.

［1］ 陆坤权，刘寄星.软物质物理学导论［M］.北京：北京大学出版社，2006

［2］ 陈洪凯，唐红梅，鲜学福等.泥石流冲击特性模型研究［J］.重庆大学学报，2010，33（5）：114～119

［3］ 陈洪凯，唐红梅，陈野鹰.公路泥石流力学［M］.北京：科学出版社，2007

［4］ 陈洪凯，唐红梅，叶四桥.中国公路泥石流研究［J］.中国地质灾害与防治学报，2008，19（1）：1～5

［5］ Chen H K，Tang H M.Essential principle of debris flow dynamics［J］.Wseas Transactions On Fluid Mechanics，2006，10（1）：932～936

［6］ 张洲波，谢洪勇，胡大鹏.颗粒在斜槽中流动的实验研究［J］.中国粉体技术，2001，7（6）：1～4

［7］ 朱鸿琛，胡林，白建勇.三维漏斗中颗粒流量及其相关因素的研究［J］.物理学报，2010，30（5）：39～42

［8］ 刘传平，王立，岳献芳 等.颗粒流本构关系的实验研究［J］.北京科技大学学报，2009，31（2）：256～260

［9］ Hungr O，Morgenstern N R.Experiments on the flow behaviour of granular materials at high velocity in an open channel［J］.Geoth，1984，34：415～421

［10］ 鲍德松，周英，张训生等.二维斜面粗糙边界附近颗粒流量密度分布［J］.物理学报，2005，54（3）：1279～1282

2011－10－19）

贵州大学SRT 项目资助（贵大SRT字（2010）101号），省长基金（黔省专合字（2010）5号）.

赵振（1989年出生），男，湖北襄阳人，贵州大学理学院电科系09级本科生.

胡林（1953年出生），女，贵州贵阳人，教授，研究方向：软凝聚态物理.