拓扑绝缘体简介

吕衍凤 陈 曦 薛其坤

（低维量子物理国家重点实验室，清华大学物理系，北京 100084）

拓扑绝缘体简介

吕衍凤 陈 曦 薛其坤

（低维量子物理国家重点实验室，清华大学物理系，北京 100084）

拓扑绝缘体是最近几年发现的一种全新的物质形态，由于其独特的能带结构，具有零质量的狄拉克费米子及其相关的奇妙物理特性，近些年来引起了人们的广泛关注.同时，它还展现出在自旋电子学和量子计算等领域巨大的应用前景.

拓扑绝缘体；量子霍尔效应；量子自旋霍尔效应；Majorana费米子

1 引言

拓扑绝缘体是最近几年发现的一种全新的物质形态，现在已经引起了巨大的研究热潮.拓扑绝缘体具有新奇的性质，虽然与普通绝缘体一样具有能隙，但拓扑性质不同，在自旋－轨道耦合作用下，在其表面或与普通绝缘体的界面上会出现无能隙、自旋劈裂且具有线性色散关系的表面/界面态.这些态受时间反演对称性保护，不会受到杂质和无序的影响，由无质量的狄拉克（Dirac）方程所描述.理论上预言，拓扑绝缘体和磁性材料或超导材料的界面，还可能发现新的物质相和预言的Majorana费米子，它们在未来的自旋电子学和量子计算中将会有重要应用.拓扑绝缘体还与近年的研究热点如量子霍尔效应、量子自旋霍尔效应等领域紧密相连，其基本特征都是利用物质中电子能带的拓扑性质来实现各种新奇的物理性质.

2 量子霍尔效应和量子自旋霍尔效应

1879年，Hall发现了霍尔效应［1］；1980年，von Klitzing在硅的金属－氧化物－半导体场效应管（MOSFET）中首次观测到整数量子霍尔效应（QHE）［2］，霍尔电导σxy＝ne2/h（n是整数）是量子化的，σxy对样品的大小、形状、载流子密度甚至迁移率均不敏感，这说明存在某种内在的不变量.1982年，Thouless等人指出，σxy对系统自身变化的不敏感性来源于QHE体系的拓扑不变性，描述它的拓扑不变量称为Chern数（用整数n表示）［3］，其能带的拓扑性与一般绝缘体截然不同：QHE态中n为非零的整数，对应量子电导前的系数；普通绝缘体，n为零.普通绝缘体和真空有相同的拓扑分类.QHE态和真空拓扑性不同，其和真空的界面上拓扑不变量必须发生变化，这导致了无能隙导电的边缘态出现［4，5］，如图1.强磁场限制了QHE的实际应用，人们开始思考利用电子的自旋自由度，在无外加磁场的情况下实现QHE，即不同自旋方向的载流子在空间上实现分离，如图2（a），从而实现零磁场下的霍尔效应——量子自旋霍尔效应（QSHE）.2005年和2006年，Kane［6］和张首晟［7］等人分别预言，利用电子的自旋－轨道耦合，在零磁场下（保持时间反演对称性）QSHE态即可实现，而实现它的体系，就是二维拓扑绝缘体.

图1

3 二维拓扑绝缘体

图2（a）是QSHE绝缘体和普通绝缘体的界面，图2（b）是二维拓扑绝缘体的能带结构.在能隙内，两支自旋取向不同的边缘态从导带一直延伸到价带，并在k＝0处相交，在交点处自旋简并.在交点附近，能量与动量关系是线性的（即E∝k）.QSHE态和QHE态类似，不管边缘态能带的形状发生什么变化，费米面始终会穿过它，体现了拓扑不变性.另外，虽然QSHE的边缘态同时具有向前和向后的通道，但非磁性杂质引起的背散射仍然是禁止的.这是因为受时间反演对称性的要求，动量相反的电子其自旋取向也相反.非磁杂质散射不能翻转自旋而破坏时间反演对称性，因而不能引起背散射.2006年，张首晟的研究组独立地提出了一种实现QSHE的一般理论，并预言了HgTe/CdTe超晶格结构可以实现 QSHE［7］.2007年，德国的Molenkamp研究组通过实验证实了这一理论预言［8］.他们通过分子束外延生长的办法制备出了不同厚度的CdTe/HgTe/CdTe超晶格，中间层的厚度d有临界宽度dc：d＜dc时，样品几乎处于绝缘态，此时作为常规半导体的CdTe起主要作用；d＞dc时，样品具有了两倍量子电导2e2/h，且与样品长度无关，如图3.时间反演不变的量子自旋霍尔系统的边缘态存在两个通道，因此中间层能带反转材料HgTe起主要作用，只有边缘态参与了导电，从而证实了它是二维的拓扑绝缘体.

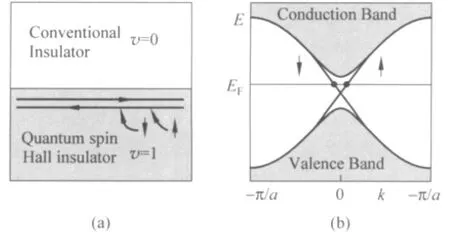
图2

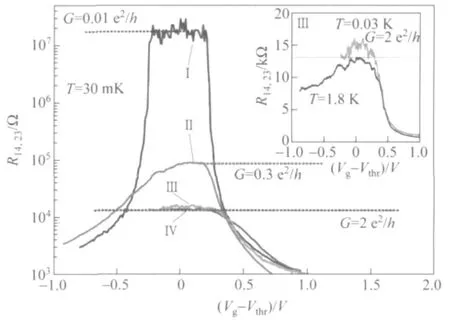
图3 GdTe/HgTe/GdTe超晶格能带翻转前（曲线Ⅰ）和能带翻转后（曲线Ⅱ、Ⅲ）的电阻变化［8］

4 三维拓扑绝缘体

2007年，Kane预言二元铋锑合金Bi1－xSbx（0.07＜x＜0.22）是一种三维拓扑绝缘体，称为强拓扑绝缘体［9］.三维拓扑绝缘体体态是绝缘的，界面上具有二维的表面态，无能隙.在其表面态的布里渊区中存在4个时间反演对称点，这些特殊点上会出现Kramers简并，形成狄拉克锥（Dirac Cone）结构，如图4（a）.狄拉克锥的顶点称为狄拉克点，狄拉克点附近能量与动量之间的色散关系是线性的，由狄拉克方程所描述.由于自旋－轨道耦合，三维拓扑绝缘体表面态的自旋始终垂直于动量方向，且无简并.受时间反演对称性保护，动量相反表面态之间的散射是禁止的.2008年，Hasan研究组利用角分辨光电子能谱（ARPES）研究了Bi1－xSbx的表面态，发现在Γ－M 之间，表面态与费米能级相交为奇数次［10］，并且表面态是自旋极化的［11］，证明了Bi1－xSbx是三维拓扑绝缘体，如图4（b）和（c）.

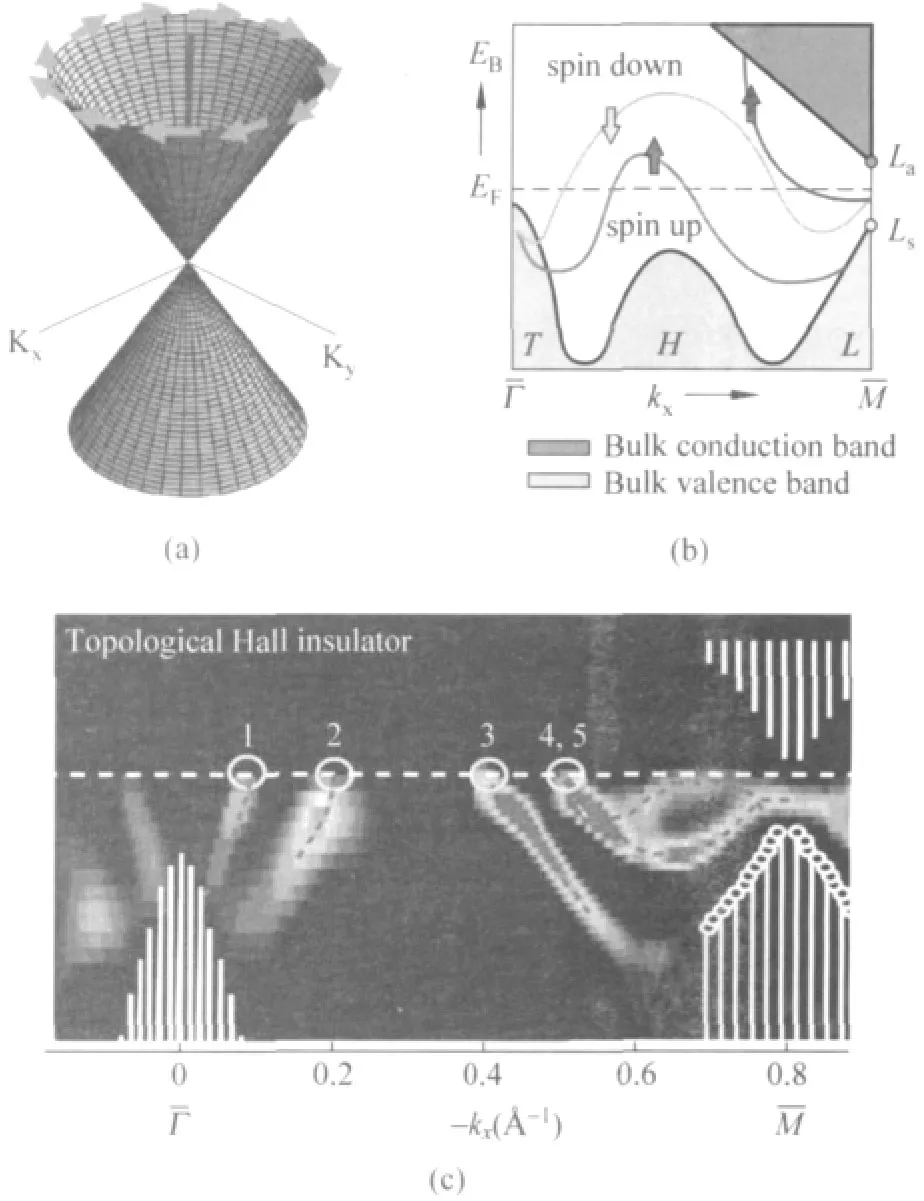
图4

2009年，中国科学院物理研究所的方忠、戴希研究员与张首晟教授合作，预言了一类全新的拓扑绝缘体：Bi2Se3、Bi2Te3以及Sb2Te3［12］.这类拓扑绝缘体具有稳定的化学配比，结构简单，易于合成；能隙很宽并且只有一个狄拉克点.几乎同时，美国普林斯顿大学的Hasan教授与Cava教授合作利用ARPES给出了Bi2Se3的能带结构［13］，验证了这一新型的拓扑绝缘体材料.Bi2Se3的能隙达到0.3eV，远远超出室温的能量尺度，抗热扰动能力强，为制备室温工作的自旋电子学器件创造了可能，被称为第二代拓扑绝缘体［14］.同年，美国斯坦福大学的沈志勋教授也验证了Bi2Te3的拓扑绝缘性［15］，并首次给出该体系雪花状的费米面结构，如图5.

图5

利用助熔剂法生长的单晶拓扑绝缘体有较高的缺陷密度，因而通常得不到真正的绝缘体.清华大学的薛其坤研究组与中科院物理所的马旭村研究组通过采用二元半导体化合物生长中经典的三温度法，利用分子束外延技术（MBE）制备出高质量的绝缘体薄膜［16］，得到了真正的绝缘体.他们还利用扫描隧道显微镜（STM）在实验上证实了拓扑表面态受时间反演对称性保护这一特性［17］，观察到了表面态的朗道量子化［18］.

5 展望

最近，中科院物理所的方忠、戴希研究组与张首晟合作，通过第一性原理计算和理论分析，发现在拓扑绝缘体材料中通过掺杂过渡金属元素可以实现量子化的反常霍尔效应［19］.通过磁性掺杂，借助Van Vleck顺磁性，可以实现磁性的拓扑绝缘体.他们发现这一磁性原子掺杂体系与一般的稀磁半导体有明显的不同，不需要有载流子，体系仍然保持着绝缘体的状态，且可以实现铁磁的长程有序态.由于掺杂原子的自旋极化与强烈的自旋－轨道耦合，在这一体系中无需外加磁场，也无需相应的朗道能级，在适当的杂质掺杂浓度和温度下，就可以观察到量子化的反常霍尔效应.在实验上观测量子化的反常霍尔效应是这一领域的一个热点.

另外，在拓扑绝缘体与s波超导的界面上，由于近邻效应，可形成拓扑超导体，此时体系电子自由度减小一半，可承载Majorana费米子.这为实验上观测这一神秘的粒子提供了可能性.2008年，Kane等人提出了在拓扑绝缘体与普通超导体的界面处有可能产生Majorana费米子［20］.由于近邻效应，库伯对可以隧穿到拓扑绝缘侧，在表面诱导出超导能隙.由于表面态是自旋分辨的，拓扑绝缘体表面形成的二维的超导态与px＋ipy的超导态类似，在其涡旋中心将产生零能量的Majorana费米子态，如图6.所不同的是，它并不破坏时间反演对称性，且其库伯对满足偶宇称，因此它不会由于微小扰动而使量子态退相干，从而导致计算错误，这使得拓扑绝缘体可以用于容错量子计算［20～22］.

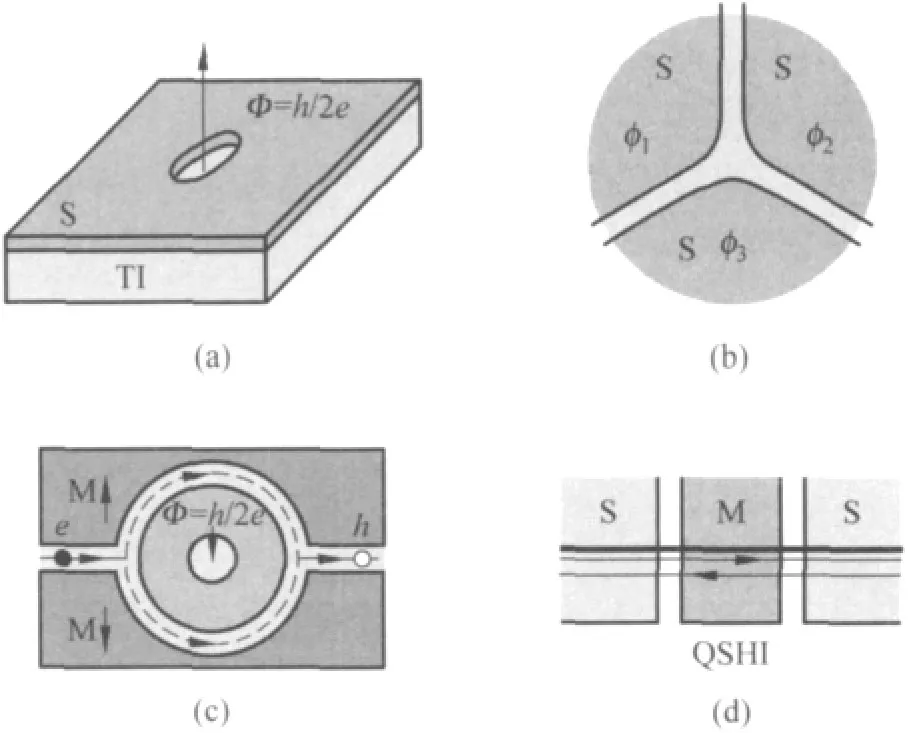
图6 不同形态超导和磁性薄膜的界面上产生的Majorana费米子［4］

在短短几年的时间里，拓扑绝缘体已经引起了巨大的研究热潮，它的理论体系已经基本建立起来，其独特的能带结构及其随层厚、电场调制等的变化也已用多种方面得到验证.拓扑绝缘体对自旋电子学、量子计算和物理基础理论等都会有重要的作用.

［1］ E.H.Hall，Am.J.Math.，2，287（1879）

［2］ K.v.Klitzing，G.Dorda，M.Pepper，Phys.Rev.Lett.，45，494（1980）

［3］ D.J.Thouless，M.Kohmoto，M.P.Nightingale，M.den Nijs，Phys.Rev.Lett.，49，405（1982）

［4］ M.Z.Hasan，C.L.Kane，Rev.Mod.Phys.，82，3045（2010）

［5］ X.－L.Qi，S.－C.Zhang，Physics Today，63，33（2010）

［6］ C.L.Kane，E.J.Mele，Phys.Rev.Lett.，95，146802（2005）

［7］ B.A.Bernevig，T.L.Hughes，S.－C.Zhang，Science，314，1757（2006）

［8］ M.König，S.Wiedmann，C.Brune，A.Roth，H.Buhmann，L.W.Molenkamp，X.－L.Qi，S.－C.Zhang，Science，318，766（2007）

［9］ L.Fu，C.L.Kane，E.J.Mele，Phys.Rev.Lett.，98，106803（2007）

［10］ D.Hsieh，D.Qian，L.Wray，Y.Xia，Y.S.Hor，R.J.Cava，M.Z.Hasan，Nature，452，970（2008）

［11］ D.Hsieh，Y.Xia，L.Wray，D.Qian，A.Pal，J.H.Dil，J.Osterwalder，F.Meier，G.Bihlmayer，C.L.Kane，Y.S.Hor，R.J.Cava，M.Z.Hasan，Science，323，919（2009）

［12］ H.J.Zhang，C.X.Liu，X.L.Qi，X.Dai，Z.Fang，S.－C.Zhang，Nat.Phys.，5，438（2009）

［13］ Y.Xia，D.Qian，D.Hsieh，L.Wray，A.Pal，H.Lin，A.Bansil，D.Grauer，Y.S.Hor，R.J.Cava，M.Z.Hasan，Nat.Phys.，5，398（2009）

［14］ J.Moore，Nat.Phys.，5，378（2009）

［15］ Y.L.Chen，J.G.Analytis，J.－H.Chu，Z.K.Liu，S.－K.Mo，X.L.Qi，H.J.Zhang，D.H.Lu，X.Dai，Z.Fang，S.C.Zhang，I.R.Fisher，Z.Hussain and Z.－X.Shen，Science，325，178（2009）

［16］ Y.Y.Li，G.Wang，X.G.Zhu，M.H.Liu，C.Ye，X.Chen，Y.Y.Wang，K.He，L.L.Wang，X.C.Ma，H.J.Zhang，X.Dai，Z.Fang，X.C.Xie，Y.Liu，X.L.Qi，J.F.Jia，S.C.Zhang and Q.K.Xue，Adv.Mater.，22，4002（2010）

［17］ T.Zhang，P.Cheng，X.Chen，J.F.Jia，X.C.Ma，K.He，L.L.Wang，H.J.Zhang，X.Dai，Z.Fang，X.C.Xie and Q.K.Xue，Phys.Rev.Lett.，103，266803（2009）

［18］ P.Cheng，C.L.Song，T.Zhang，Y.Y.Zhang，Y.L.Wang，J.F.Jia，J.Wang，Y.Y.Wang，B.F.Zhu，X.Chen，K.He，L.L.Wang，X.Dai，Z.Fang，X.C.Xie，X.L.Qi，C.X.Liu，S.C.Zhang and Q.K.Xue，Phys.Rev.Lett.，105，076801（2010）

［19］ R.Yu，W.Zhang，H.J.Zhang，S.C.Zhang，X.Dai and Z.Fang，Science，329，61（2010）

［20］ L.Fu，C.L.Kane，Phys.Rev.Lett.，100，096407（2008）

［21］ L.Fu，C.L.Kane，Phys.Rev.Lett.，102，216403（2009）

［22］ J.C.Y.Teo，C.L.Kane，Phys.Rev.Lett.，104，046401（2009）

INTRODUCTION TO TOPOLOGICAL INSULATOR

LüYanfeng Chen Xi Xue Qikun
（State Key Laboratory of Low－Dimensional Quantum Physics，Department of Physics，Tsinghua University，Beijing 100084）

Topological insulator is a new form of matter discovered in recent years and has attracted extensive attention due to its unique band structure，zero－mass Dirac fermion and related novel physical properties.It also shows great application prospect in spintronics and quantum computation.

topological insulator；quantum Hall effect；Quantum spin Hall effect；Majorana fermion

2011－11－21）