关于两个导体球间的电容问题

卓冯骏 花修坤 李成金

（苏州大学物理科学与技术学院，江苏 苏州 215006）

关于两个导体球间的电容问题

卓冯骏 花修坤 李成金

（苏州大学物理科学与技术学院，江苏 苏州 215006）

本文利用镜像法，计算了两相互接触的带电导体球的电容.接着再用镜像法计算两相距一定距离的具有相同半径的导体球间的电容，且其极限情况与已知结果相同.然后用Matlab对结果进行了数值分析.

镜像法；导体球；电容

1 两个相互接触的孤立带电导体球的电容

两个相距一定距离的带电导体球之间电容的计算是个基本问题，但在普通物理电磁学中却鲜见.在《费恩曼物理讲义》（第 二 卷）［1］中用镜像法解决了带电导体球与球外一点电荷之间的电场和电势分布问题.如图1所示，半径为a的接地导体电势由点电荷q及其在球内的像电荷q′共同产生，其中像电荷q′的大小及距球心的位置分别为

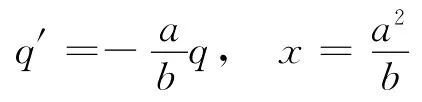
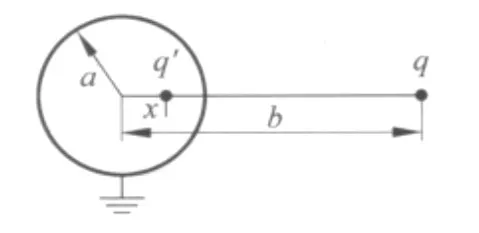
图1

如果导体球电势不为零，情况会发生变化.假设导体球原来不带电且绝缘，现将一个正的点电荷置于其附近.同前面一样通过用像电荷q′，且除此之外在球心再加上一个电荷q″而找到解.当选取：时，不仅使球保持了电中性，又保证了球面等势，在球外每一处的场就由q，q′与q″的场叠加而成.

现在我们考虑两个相接触的孤立带电导体球的电容问题.

文献［2］利用镜像法、差分法对两个接触球孤立带电导体的电容进行了计算，这里我们用一般的数列和级数求解.

如图2所示，两个半径为R的导体球相互接触，总电荷为Q.静电平衡后两导体球等势，设其电势为U.

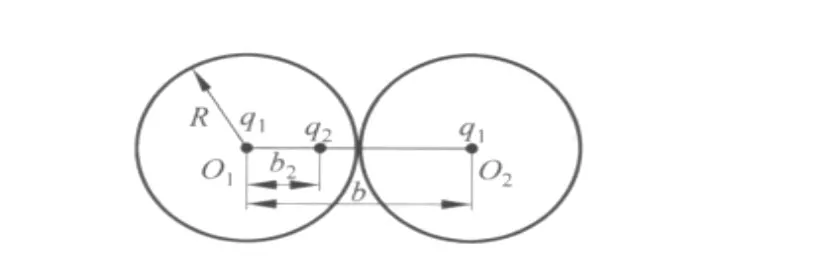
图2

为了使各球面等势，我们在O1，O2处分别放置镜像电荷q1，且q1满足

但此时O2球内的q1破坏了O1球的等势条件，同时O1球内的q1也破坏了O2球的等势条件，为了消除两者之间的影响，我们先在O1球内距球心b2放置一镜像电荷q2，以消除O2球内的q1对O1球表面等势的影响，由第一部分的结论我们可以知道q2，b2满足关系

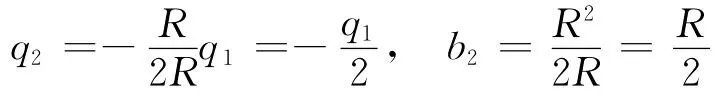
同理需在O2球内距球心b2位置放置相同镜像电荷q2，但是，两球内的q2同时又破坏了对方的等势条件，因此，我们需分别在距两球心b3处放置镜像电荷q3消除其影响，再引用第一部分的结论可知

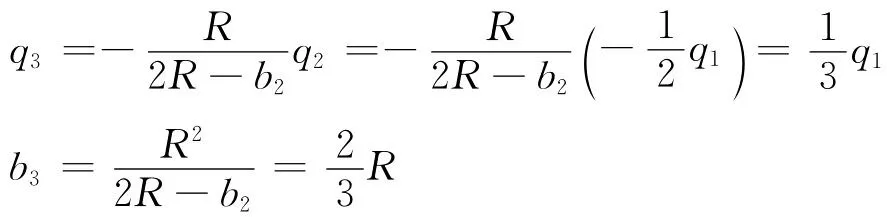
如此反复做下去，分别放置电荷q4，q5，…，qn满足

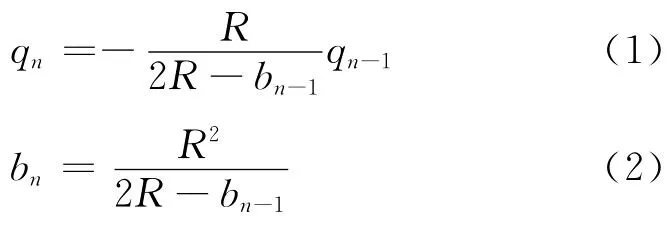
由上两式可得

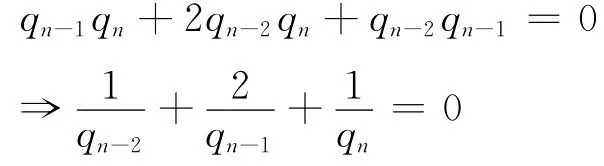
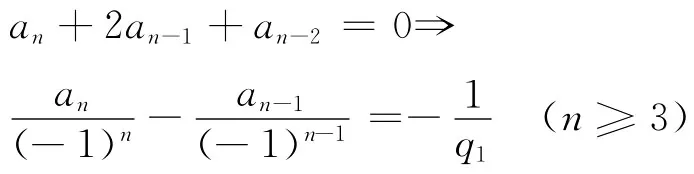
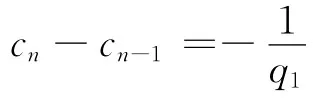
解此数列得

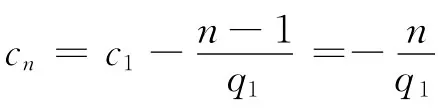
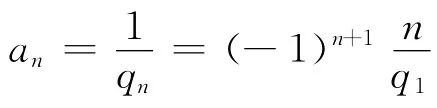
最终得到qn的通式

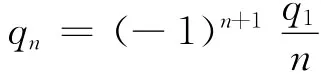
为了使两导体球所带总电荷保持不变，所加镜像电荷总和应等于初始总电荷，即有关系

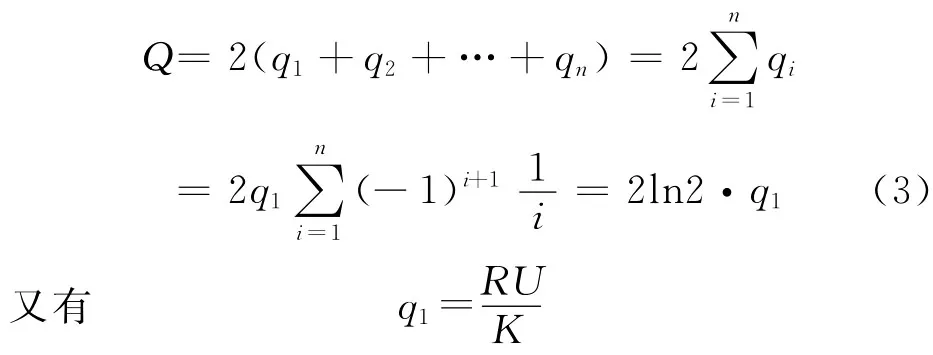
故

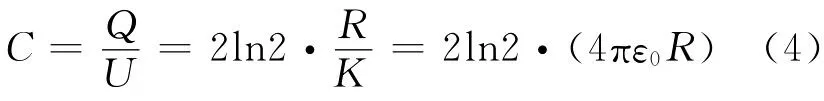
2 两个分离导体球间电容

在文献［4～6］中运用镜像法计算并讨论了两导体球间的相互作用力问题，在这里我们使用上述的方法求解两导体球间的电容.如图3，两半径为R的导体球O1，O2相距为b，设分别带有电荷＋Q，－Q，由对称性分析可知它们的对称面 MN为等势面，两球与MN面的电势差大小相等，不妨设两球电势分别为＋U，－U.分别在O1，O2处置电荷q1，，满足

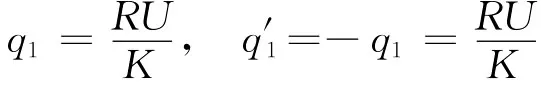
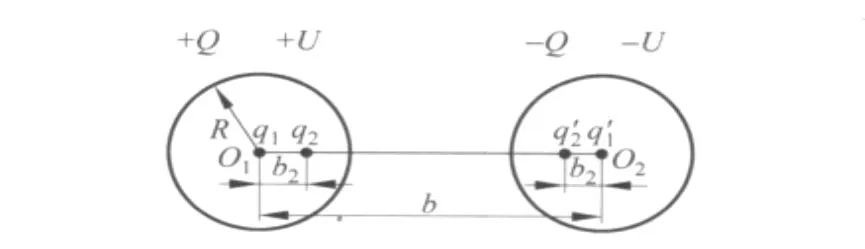
图 3

在距O1点b2处放置电荷q2，消除对O1球电势的影响，有

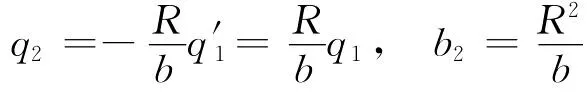
同时再在距O2点b2处放置电荷，消除q1对O2球电势的影响，有

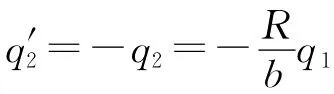
同理在距O1点b3处放置电荷q3，消除对O1球电势的影响，在其对称位置上放置电荷，满足

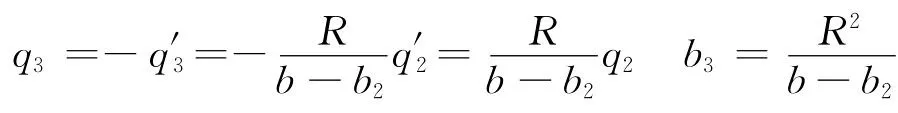
如此反复做下去，分别放置电荷q4，q5，…，qn，满足

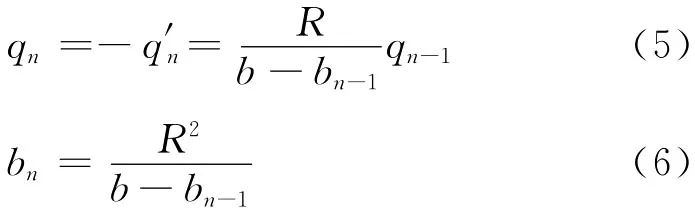
同第一部分的方法可得（具体步骤见附录）：

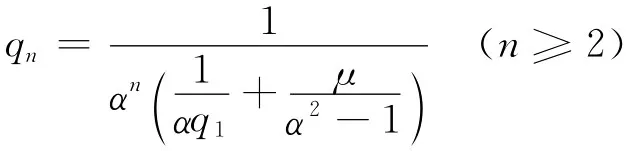
其中

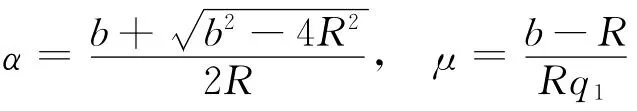
对qn求和并代入q1得

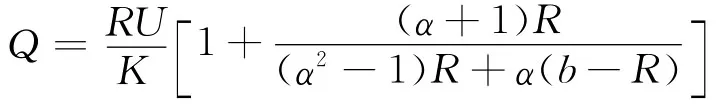
两球电势差为2U，根据电容定义得

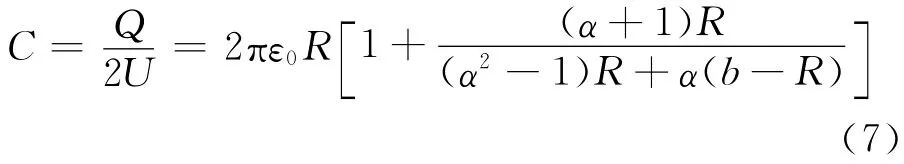
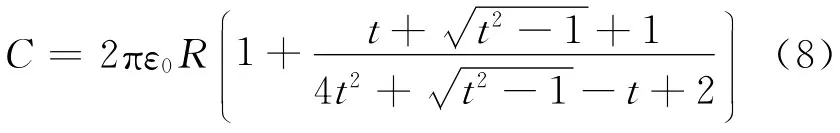
式（8）即为所求电容的解析表达式.

3 对结论的论证与分析

在极限情况（即b≫R）下应用电磁学的方法求出两导体球间电容，与式（8）取极限得到的结果进行对比.

由于b≫R，可忽略两球的相互影响，利用电势叠加原理得两球的电势分别为

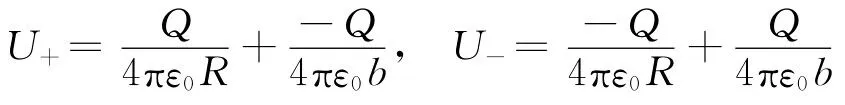
依电容定义得

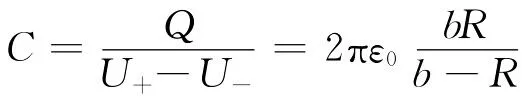
最后我们使用Matlab7.X数学软件对式（8）进行数值计算，并绘制出C（R，b）与t的关系图.

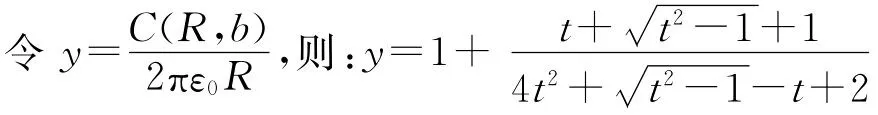
定量结果如表1.

由表1可以看出，随着t值的不断增加，y逐渐接近于1，且曲线逐渐平缓.

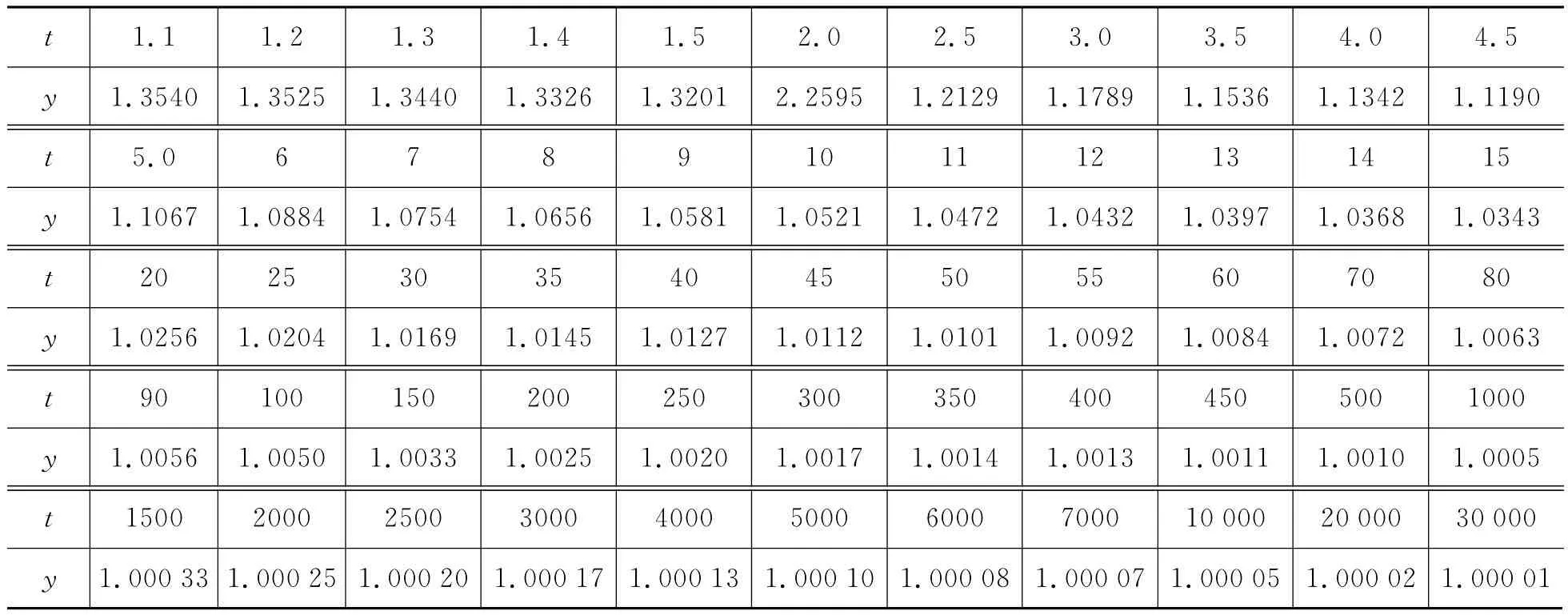
表1 y－t取值表

图4为 Matlab7.X所作的t－y图像，从图像中可以得到与定量分析相同的结果.

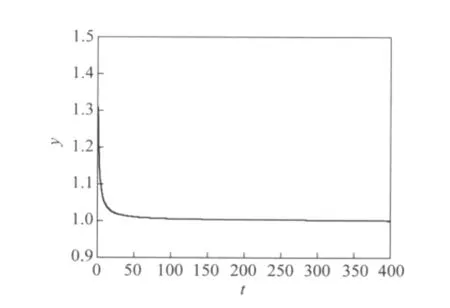
图 4

4 结束语

正如文献［3］中提到的：电容器的电容与两导体的尺寸、形状和相对位置有关，与所带电量和电势差无关.从上述分析可以看出，当b不断增大时，两导体球的电容逐渐减小，最终趋向于稳定值.本文应用镜像法这一直观的物理方法，给出了两半径相等导体球电容的解析表达式.对于半径不同导体球间的电容可按照类似的方法同样求解对应的数列，但是最终得到的结果不是解析解.当然，求解此问题的方法还有很多，比如利用双球面坐标系计算［7］.

［1］ R.P.Feynman.费恩曼物理学讲义（第二卷）［M］.郑永令，华宏鸣，吴子仪等译.上海：上海科学技术出版社，2005.77－78

［2］ 童国平.两个接触球孤立带电导体［J］.浙江师范大学学报（自然科学版），1989，（2）

［3］ 赵凯华.电磁学（上册）［M］.北京：高等教育出版社，1985.154～156

［4］ 郑焕武.两带电导体球外的电势分布和相互作用力问题［J］.西昌学院学报（自然科学版），2008，（4）

［5］ 欧红叶，胡先权.两个带电导体球之间相互作用力的计算［J］.重庆师范学院学报（自然科学版），2003，（2）

［6］ 丁锐猛，陈乃强.关于两个带电导体球相互作用问题力的讨论［J］.大学物理，1985，（4）

［7］ 赵先林，李金铭.关于两个带电导体球相互作用力问题的讨论［J］.河南教育学院学报（自然科学版），2000，（4）

附录

（6）/（5）得

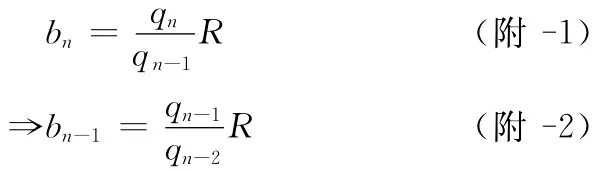
将（附－2）代入式（5）得

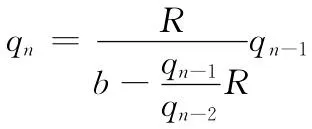
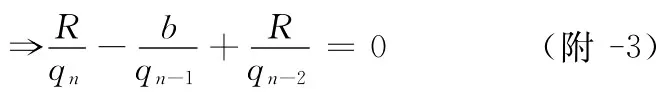
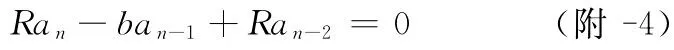
设其满足

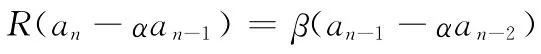
其中α，β为待定常系数，化简得

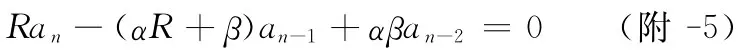
由待定系数法得到α，β满足

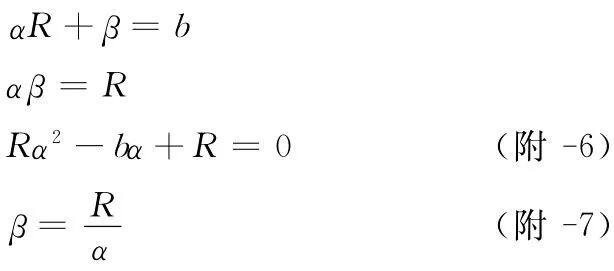
解（附－6）得

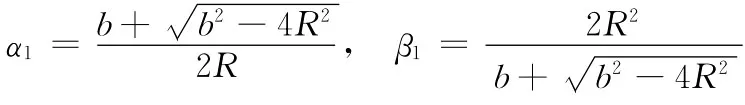
另有一组解为

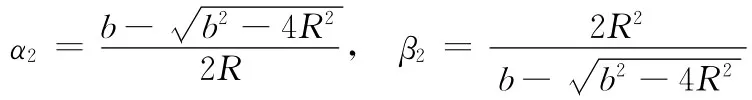
（附－5）式的解可表示为

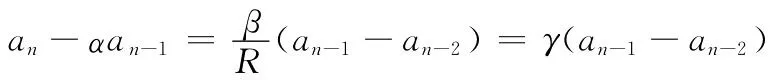
其中

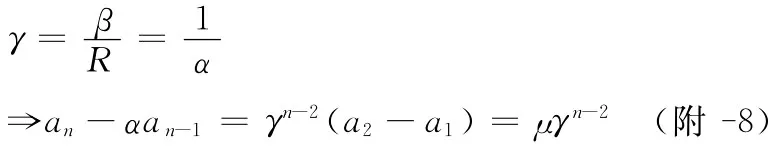
将（附－8）式左右都除以αn得

对于α1，若成立，可得到：b＞2R，显然成立.

对于α2，若成立，可得到：b＜2R，舍去，最终满足要求的解为

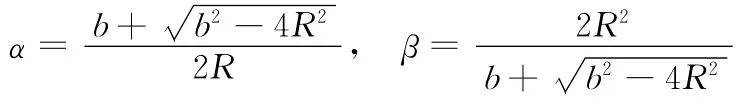
式（附－9）化为

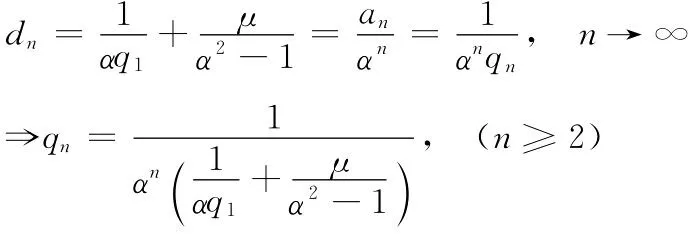
因带正电导体球的总电荷保持初始值不变，故有

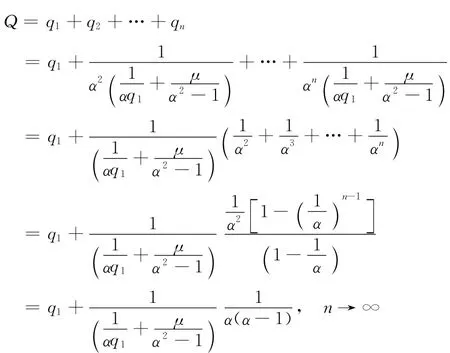
代入μ和q1进一步化简得到

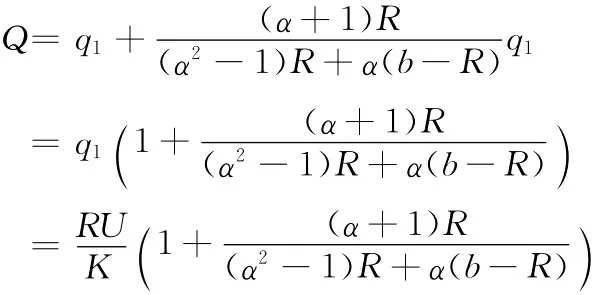
CAPACITANCE PROBLEM BETWEEN TWO CONDUCTING SPHERES

Zhuo Fengjun Hua Xiukun Li Chengjin
（School of Physics and Technology，Soochow University，Suzhou，Jiangsu 215006）

In this paper，by the image method，we calculated the capacitance between two contacting conducting spheres with the same radius，and the capacitance between two separated conducting spheres with same radius，equal charge but opposite signs.Its limited situation is the same as the known result.The results were analyzed with Matlab.

image method；conducting sphere；capacitance

2011－11－21）

卓冯骏（1991年出生），江苏淮安人，现就读于苏州大学物理科学与技术学院2009级.