基于累积误差效应的瞬变加注量融合算法
2012-12-19王新峰王洪志高敏忠
王新峰 王洪志 高敏忠
(中国酒泉卫星发射中心,酒泉732750)
推进剂加注是火箭起飞前一项重要而又危险的工作,为了保证火箭能将有效载荷送至预定轨道同时又不至于造成过多推进剂浪费污染,对推进剂的加注精度往往要求很高.为更好地完成地面加注系统的推进剂加注工作,实时准确计量加注量,在系统原来单一的接触式流量计(氧化剂为涡街流量计,燃烧剂为涡轮流量计)基础上新增两路加注量测量设备,一路是非接触式的超声波流量计,另一路是高精度液位计.前者安装于推进剂加注管道的外壁,和原有接触式流量计一样通过累积方式得到实时加注量数据,而后者通过连通器原理安装在推进剂贮罐上,并事先通过液位-体积关系标定获取任一液位对应的加注量数据.通过对同一时刻获取的三路累积加注量(以下简称加注量)数据进行某种算法的数据融合,给出一个精度更高的加注量数据供加注系统工作人员决策参考.目前常用的数据融合方法可以分为随机和人工智能两大类,其中随机类方法有加权平均法、卡尔曼滤波法、极大似然估计法、D-S证据理论等[1~8].目前加权平均算法大多都是假设各传感器对常值或缓变参数进行同步测量再进行数据融合[1,9~10],且通常认为多路传感器的误差特性相同,只是精度不等.本文拟采用动态加权融合算法,但本文应用背景中推进剂加注瞬时流量大(最大可达40L/s),加注量变化迅速,并且三路流量计量设备之间的误差特性不尽相同,怎样实施对不同误差效应的瞬变加注量进行数据融合是本文要研究的内容.
1 加注量计量模型
多路数据进行融合时,要求多路数据必须代表同一物理量,不妨设Xi(i=1,2,3)代表同一时刻三路流量计量设备输出的加注量测量数据,且三路设备均正常工作.测量数据可以看作是被测量值的真值与噪声干扰信号叠加的结果,即
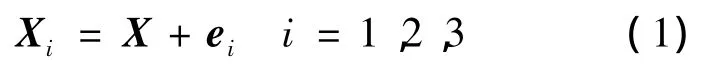
式中,X表示真值;ei表示噪声信号即误差信号;它包含设备内部噪声(过程噪声)和环境噪声(测量噪声).假设各设备的噪声为相互独立且服从均值为 0,方差为的正态分布的高斯白噪声[11],这样各测量值Xi相互独立且都是真值X的无偏估计,且测量方差为σ2i.
对于原接触式流量计和新增的超声波流量计,由于是利用二次仪表进行脉冲计数方法来计量加注量,其计量结果是在上一采样时刻计量结果的基础上累加得到的,即当前k时刻输出的加注量数据可表示为
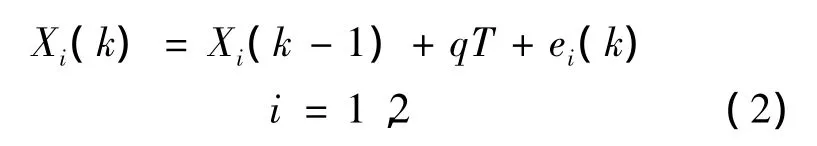
式中,q为加注过程中某一阶段推进剂瞬时体积流量;采样周期为T,式(2)递推下去可得
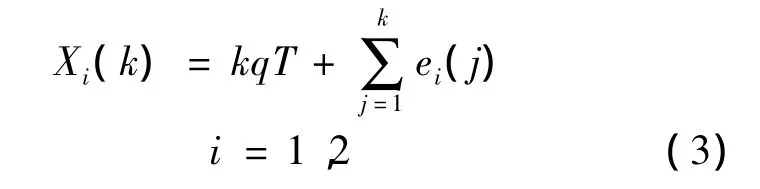
通过式(2)可以看出当前时刻的加注量与前一时刻的加注量有关,它是在前一时刻加注量的基础上增加一个体积增量qT和一个误差ei(k),式(3)表明最终加注量的计量误差是当前时刻及此前的历次计量时刻的误差总和,相当于在加注量真值基础上叠加一系列误差特性相同的干扰信号,即总的误差特性具有累积效应.但液位计所计量的推进剂加注量与原接触式流量计及超声波流量计有所不同,它始终是根据当前时刻的液位值及初始时刻的液位值来计算加注量的(事先进行液位-体积关系标定,具体此处略),与前一时刻的液位值无关,因此当前时刻的加注量也就与前一时刻加注量无关,其加注量可表示为
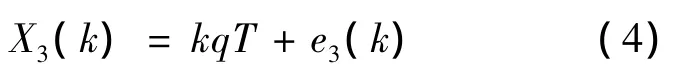
可见液位计给出的加注量计量误差没有累积效应,每一采样时刻计量值都相当于在真值上叠加一个相同统计特性的误差信号,误差信号只有一个,没有叠加,这是与式(3)的本质区别所在.
2 融合算法
测量前一般很难准确知道各路设备的测量方差,如果靠先验知识指定常常由于缺乏适应性而使融合效果不理想[1];如果利用多路设备大量的实测数据来估计方差参数,效果往往会更好.因此为了得到实时的加注量融合结果,避免过度依赖某一路数据,必须首先估计各路测量数据中误差信号的方差.根据时间域估计法[12]对式(1)有
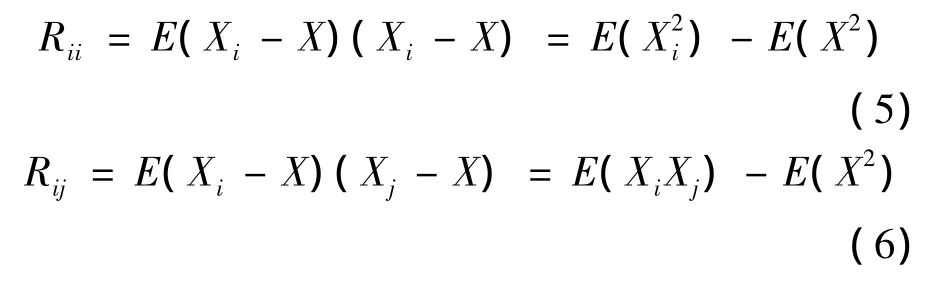
两式相减得
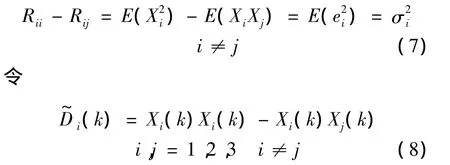
则实时方差估计值为
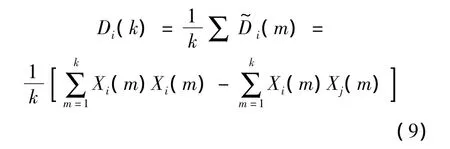
其递推形式为
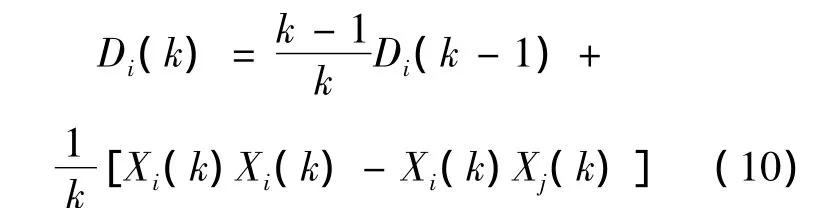
对第1路(原流量计)的测量数据,将式(3)代入式(8)中得
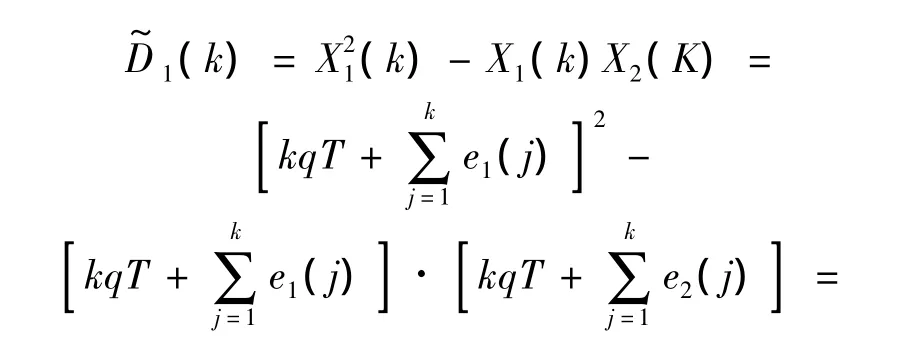

因为ei,ej(i≠j)为相互独立的高斯白噪声,则有
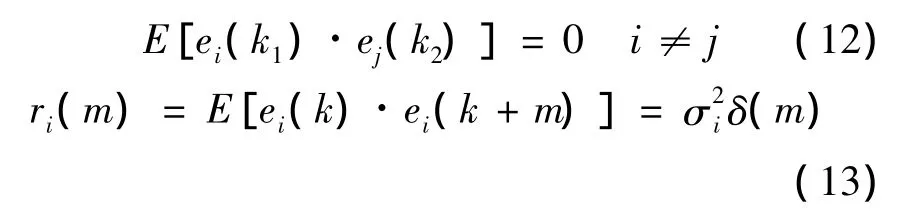
假定 ei与瞬时流量 q无关,将式(12)、式(13)代入式(11)中并取数学期望可得
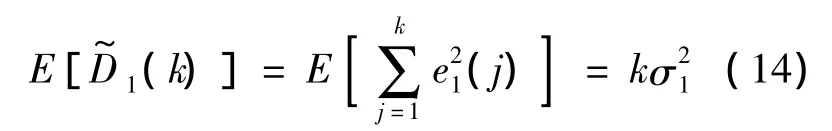
可见对于原流量计和超声波流量计而言,虽然在每一个采样周期T内的加注量增量的误差信号是ei(i=1,2,3),其方差特性不变,但从各自的累积加注量Xi(k)来看,其误差信号的统计特性则是随时间k而变化的,其误差存在累积效应,随着采样时刻的增大,误差信号的统计特性会逐渐恶化,方差扩大,计量精度下降.这也意味加注量的实时方差的数学期望将不断变化,前后相邻两个时刻“量级”不等,第k次采样融合时刻的具有的量级,因此有
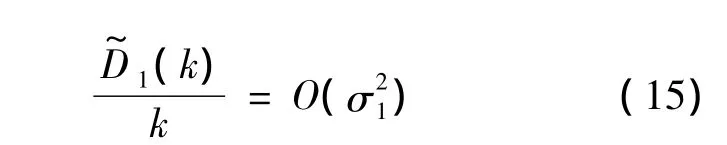
对于液位计给出的加注量,将式(4)代入式(8)中并利用式(12)可得
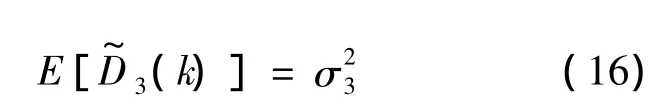
可见由于没有累积误差,液位计给出得加注量数据的实时方差是等量级的.
设已求出误差信号ei的方差σ2i前一时刻的估计值Di(k-1),并已知当前时刻的 D~i(k),则当前时刻方差的估计值可写成如下迭代形式:
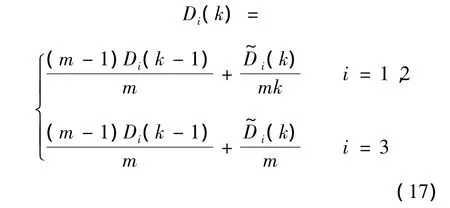
其中参数m满足1≤m≤k,当m=1表示方差估计值只利用当前时刻的实时值,而不利用历史数据;而当m=k时则表示以历次时刻的或的算术平均值作为当前时刻的方差估计值.即m不同,表示对历次的或取不同的加权值.理论上应当取m=k,因为这样才是统计上的真正估计.当采样次数k趋于无穷大时,方差估计的效果理论上会越来越好.但实际并非如此,由式(17)可以看出,当k增大到一定时,当前时刻的新数据对估计值Di(k)的贡献几乎为0,起不到修正的作用了,这是数据饱和造成的[13].究其原因,是因为对历史数据均同样对待,没有加以区别;另外如果m恒为k,会导致其参数跟踪能力下降,因为在实际中,噪声特征并不是一成不变的,随着系统长时间运行,系统参数会发生缓慢的变化,噪声特征也会发生某种程度的“缓变”,为了改善这点不足,降低数据饱和影响,提高融合算法的适应性,通过加矩形窗的数据截取方式[13-14],即始终只对最近的一批连续数据进行处理计算,而舍去这之前的历史数据,这样做需要存储每一组历史数据,当数据量很大时,对计算机资源消耗较大,例如在当前加注任务中如果融合周期设为1s,则每次大约需要存储5000~6000组历史数据;为了节省资源,增强其实时数据处理能力,原流量计和超声波流量计可按下面公式进行递推计算:
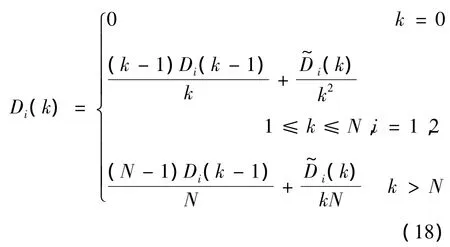
其中N为数据窗宽度,而液位计则按下式计算:
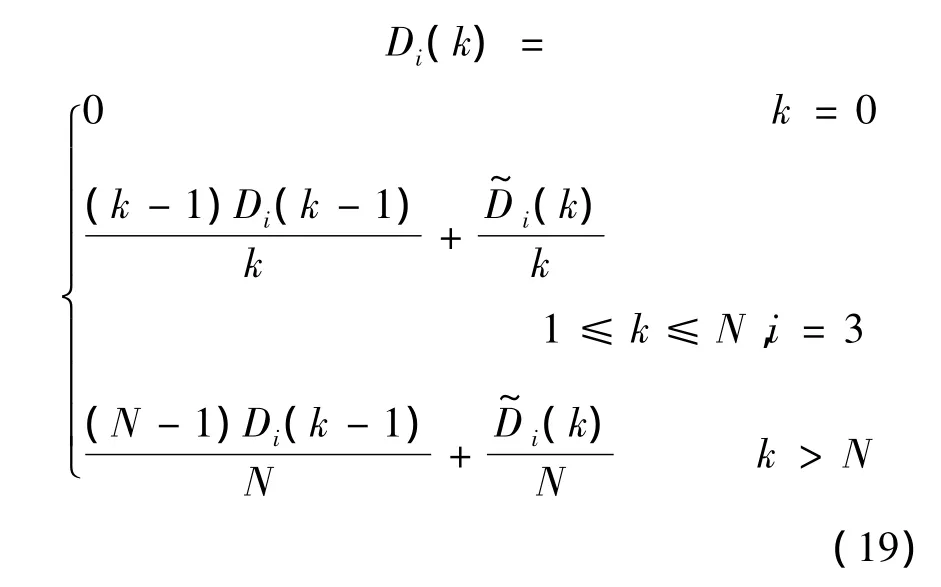
根据多次实际数据分析,N=1 200~1 500比较合适,这样只需存储前后两个时刻的数据即可.值得注意的是当采样次数k较小时,计算中可能会出现Di(k)为负值的情况[15],为保证方差永远是正数,应当取绝对值.上面求出的Di(k)是k时刻时的估计,则到第k个采样时刻时根据式(14),原流量计和超声波流量计给出的加注量的方差估计为kD1(k)和kD2(k),而液位计给出的加注量方差估计为D3(k),根据融合结果的方差最小这一约束条件下很容易通过最小二乘法[1,9]求出最优的实时加注量动态加权融合结果为
相应的最优动态加权系数为
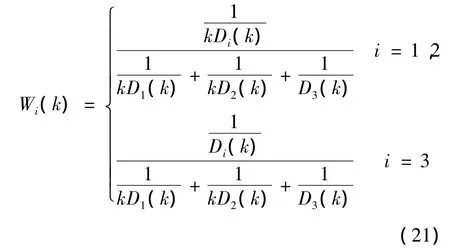
从上述推导可看出求得的Di(k)是的无偏估计,该算法中参与方差估计和最后数据融合的均是加注进程中的实时累积加注量Xi(k)(i=1,2,3),它是随时间而变化的瞬变参数.
3 实际应用
为检验该融合算法的实际效果,将其应用于某次试验任务的氧化剂(N2O4液体)加注过程,采样周期设置为1 s,数据窗宽度为1 500,原始计量数据及其融合结果与加注量的理论值偏差对比情况如表1所示.
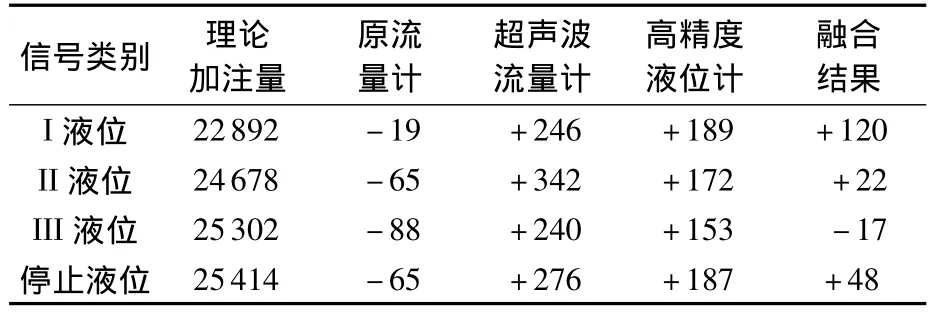
表1 三路加注量数据及其融合结果与理论值的偏差对比 L
I~III液位为火箭推进剂贮箱3处液位标记,其对应的体积已在加注前标定好,认为是对应液位处的加注量理论值.从表1中可以看出,虽然新增的两路测量设备精度较原流量计低,但经数据融合给出的加注量仅I液位处与理论值的偏差(+120 L)较原流量计偏大、较超声波流量计和高精度液位计偏小,其余液位处融合结果的偏差均较三路原始数据小,最终精度较到了0.19%,较三路测量设备中精度最高的原流量计提高了26%.这表明随着加注进程推进、采样数据增多,融合算法给出的方差估计趋于稳定和准确,最终停止液位处的加注量融合结果的偏差较原始三路加注量测量设备小,精度高.
4 结论
根据测量原理对加注系统的三路加注量测量设备测得的加注量数据进行了分析,指出了其典型的特性在于其数据的瞬变特性和误差的累积效应;通过推导各加注量数据误差的方差估计算法,给出了基于方差最优的动态加权融合结果,并经实际应用证明了该算法可以有效抑制累积误差的不断扩大趋势,给出精度优于三路原始测量数据的加注量融合结果,可以为加注系统及相关工作人员提供重要的决策参考依据.
References)
[1]仲崇权,张立勇,杨素英,等.基于最小二乘原理的多传感器加权融合算法[J].仪器仪表学报,2003,24(4):427 -430 Zhong Chongquan,Zhang Liyong,Yang Suying,et al.A weighted fusion algorithm of multi-sensor based on the principle of least squares[J].Chinese Journal of Scientific Instrument,2003,24(4):427-430(in Chinese)
[2]John Daye Z,Jessie Jeng X.Shrinkage and model selection with correlated variables via weighted fusion[J].Computational Statistics & Data Analysis,2009,53(4):1284 -1298
[3]Ting Li Chien,Jyh Hwa Tzou,Wang Chun Chieh,et al.Detection system of a security robot using multisensor fusion algorithms[J].Artificial Life and Robotics,2009,14(2):247 -251
[4]Wenzel T A,Burnham K J,Blundell M V.Dual extend Kalman filter for vehicle state and parameter[J].Vehicle System Dynamics,2006,44(2):153 -171
[5]蒯冲,龚剑扬,那云啸,等.基于极大似然估计的最优航迹融合方法[J].哈尔滨工程大学学报,2003,24(4):419 -421 Kuai Chong,Gong Jianyang,Na Yunxiao,et al.Optimal track fusion based on maximum likelihood estimate[J].Journal of Harbin Engineering University,2003,24(4):419 - 421(in Chinese)
[6]胡丹丹,肖书明,王燕清,等.基于多传感器的数据融合技术[J].东北电力学院学报,2004,24(1):62 -67 Hu Dandan,Xiao Shuming,Wang Yanqing,et al.Data fusion technique based on multi-sensor[J].Journal of Northeast China Institute of Electric Power Engineering,2004,24(1):62 -67(in Chinese)
[7]胡士强,张天桥.多传感器在线自适应加权融合跟踪算法[J].北京理工大学学报,2002,22(1):117 -120 Hu Shiqiang,Zhang Tianqiao.An on line adaptive weighted fusion algorithm for multi-sensor tracking [J].Journal of Beijing Institute of Technology,2002,22(1):117 -120(in Chinese)
[8]宋建勋,张进,吴钦章.基于D-S证据理论的多特征数据融合算法[J].火力与指挥控制,2010,35(7):96 -98 Song Jianxun,Zhang Jin,Wu Qinzhang.The algorithm of multifeature data fusion based on D-S theory of evidence[J].Fire Control& Command Control,2010,35(7):96 -98(in Chinese)
[9]翟翌立,戴逸松.多传感器数据自适应加权融合估计算法的研究[J].计量学报,1998,19(1):69 -75 Zhai Yili,Dai Yisong.Study of adaptive weighted fusion estimated algorithm of multisensor data[J].Acta Metrologica Sinica,1998,19(1):69 -75(in Chinese)
[10]吴成东,刘宗富.多传感器数据最优融合[J].传感器技术,1994,13(3):21 -24 Wu Chengdong,Liu Zongfu.The optimization of multi-sensor data[J].J Sensor& Transducer Techno,1994,13(3):21 -24(in Chinese)
[11]Richardson J M,Kenneth A M.Fusion of multisensor data[J].The International Journal of Robotics Research,1988,7(6):78-96
[12]杨位钦,顾岚.时间序列分析与动态数据建模[M].北京:北京工业学院出版社,1986:37-89 Yang Weiqing,Gu Lan.Time series analyzing and dynamic data modeling[M].Beijing:Beijing Institute of Industrial Press,1986:37-89(in Chinese)
[13]翁思义.自适应控制系统[M].北京:水利电力出版社,1995:43-46 Weng Siyi.Adaptive control system[M].Beijing:China Water-Power Press,1995:43 -46(in Chinese)
[14]胡广书.数字信号处理-理论、算法与实现[M].北京:清华大学出版社,1997:320-327 Hu Guangshu.Digital signal processing-theory,algorithm and implement[M].Beijing:Tsinghua University Press,1997:320-327(in Chinese)
[15]赵晋,张建秋,高羽.迭代异方差估计及其在多传感器数据融合中的应用[J].电子学报,2008,36(10):1938 -1943 Zhao Jin,Zhang Jianqiu,Gao Yu.Iterative heteroscedastic variance estimation with its application for multisensor data fusion[J].Acta Electronica Sinica,2008,36(10):1938 - 1943(in Chinese)
