具有容错特性的两层数据流聚类方法
2012-12-19由育阳朱纪洪
由育阳 朱纪洪
(清华大学计算机系,北京100084)
杨志宏
(中国医学科学院药用植物研究所,北京100193)
近年来数据流环境下的聚类研究工作广泛展开,具有代表性的相关研究包括基于k-median聚类思想的LOCAL SERACH算法和在此基础上进行改进的STREAM 聚类算法[1].文献[2]将密度聚类与网格聚类联合应用,提出了基于密度和网格技术的数据流实时聚类算法D-Stream,实现了数据流环境下的高效密度聚类,相关研究被认为是近年来数据流聚类技术的重要发展.文献[3]首次提出了进化数据流聚类框架CluStream,其基本思想是将聚类过程分为在线的微观聚类(mi-cro-cluster)过程和离线的宏观聚类(macro-cluster)过程,CluStream算法是一种通用的数据流聚类算法,用户可以根据不同处理需求在算法基础上进行多种方式的扩展分析,该算法灵活的扩展性是其受到广泛关注的主要原因之一.CluStream同样存在一些缺点:首先更适合对球形数域空间进行聚类,然而在真实世界数据流中聚簇往往具有非凸的空间形状;其次对于含有大量噪声的原始数据适应性较差;最后需要预先指定聚簇数量,极大的影响了原始数据聚簇的形态分布.针对以上问题在CluStream算法的基础上提出了HPStream算法[4],采用高维投影和衰减函数来适应对高维数据流的挖掘,但是仍然需要用户预先指定平均聚类数目.
本文提出了一种具有容错特性的数据流网格密度聚类算法FTGDStream(Fault-Tolerant Grid-Density Clustering over Data Stream),设计了一种新的概要数据结构HLSFTS(Hierarchical Lifting Scheme Fault-Tolerant Synopses),利用概要结构的单次扫描、高压缩和容错程度可控的特点对新数据点和聚类中心点进行容错度量.在FTGDStream二层框架聚类算法的第1过程中,在线微观聚类要求算法对原始数据流进行单次扫描就可以高效的构造小波概要数据结构.在第2过程中,聚类算法在离线状态下进行,无需等待数据积累到希望的规模才进行一次性处理.
1 相关概念
现有的相关研究已经证明任意的传统小波都可以采用惰性提升的方法经过有限次的提升和对偶提升后乘以一个常数得到[5].
定义1 若(h,g)构成补,则h的任何其他补g′(z)都可以表示为 g′(z)=g(z)+h(z)s(z2),其中s(z)为Laurent多项式.
定义2 若(h,g)构成补,则g的任何其他补h′(z)都可以表示为 h′(z)=h(z)-g(z)t(z2),其中t(z)为Laurent多项式.
惰性提升的基本思想是首先将输入信号分成奇偶2部分,由偶数项组成信号的低频部分,奇数项组成原始信号的高频部分,然后对低频和高频2个数据序列做有限次提升和对偶提升后乘以某常数.
定义3 存在2个数据流片段 Dx={dx,1,dx,2,…,dx,n}和 Dx+1={dx+1,1,dx+1,2,…,dx+1,n},定义相似性函数形如 S(Dx,Dx+1),如果 S(Dx,Dx+1)≤δ成立,其中δ为由用户设定的正常数,则称2个数据序列Dx和Dx+1在以δ为边界的情况下具有相似性.
相似性函数 S(Dx,Dx+1)满足如下关系[6]:
1)正定性,S(Dx,Dx+1)≤0;
2)对称性,S(Dx,Dx+1)=S(Dx+1,Dx);
3)三角不等关系,S(Dx,Dx+1)≤S(Dx,Dx+2)+S(Dx+1,Dx+2).
用户设定的δ通常在(0,1]内取值,当取δ=0时表示Dx和Dx+1完全相同,当 δ→1时表示 Dx和Dx+1相似性越小.相似性度量通常与度量相似模式之间的距离联系在一起,最常用的距离度量方法为Minkowski距离,定义如下:
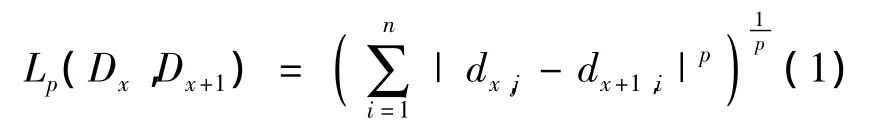
Minkowski距离是对欧几里得距离的推广,当取p=2时即为欧几里得距离,当取p=1时为Manhattan距离,当取p=∞时为最大距离度量.基于距离的度量方法计算量小且算法效率相对较高,经过简单的加权处理就可以实现对平行移动、拉伸或压缩、振幅放大或压缩和有限趋势叠加的数据序列进行相似性度量.
2 二层容错聚类
2.1 HLSFTS 概要构造
设概要结构分为l层,每层概要结构代表长度为L的原始序列则存在Ll=Ll-1=…=L1,每一层都保留了数目远小于次级层次的小波系数,l越大HLSFTS对原始序列的压缩水平越高.
定义4 当前窗口中的数据序列为P,定义提升小波容错概要的分辨率为r=P/2i,i为小波误差树的层数.
显然提升小波容错概要结构的分辨率决定了如何对原始数据流进行子序列划分.
定义5 提升小波容错概要结构为一个四元组(t,n,ft,ls),其中 t是概要结构的时间戳,n 是原始数据流中的数据个数,ft是概要的相似性度量,ls是提升小波概要数据结构.
每层小波误差树的分辨率不同,原始序列数据个数n也不同.相似性度量ft可以定义多种度量方式.ls代表提升小波概要数据结构.提升小波概要数据结构的小波系数选择可以采用不同的误差度量准则,小波系数的正规化方法采用重构误差采用衡量.
HLSFTS构造流程如图1所示.
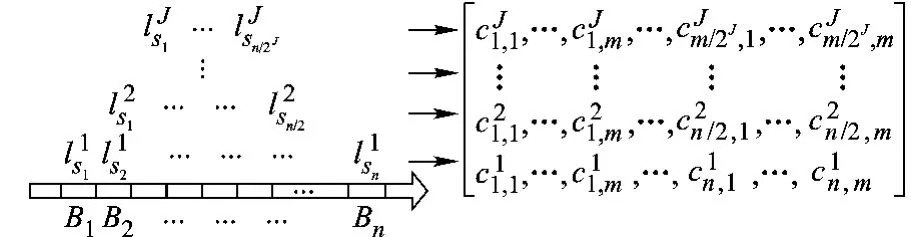
图1 HLSFTS构造流程
以Haar小波为参照,每个惰性提升小波概要结构的构造算法计算时间复杂度至多不会超过O(N(logN)log m),算法的空间复杂度至多不会超过O(N),HLSFTS概要数据结构由至少1个最多|B|个提升小波概要结构构成,重复进行最少|B|次最多|B|+|B|/2+…+|B|/2J次的提升小波变换,所以 HLSFTS空间复杂度最大为O(|B|×N).时间复杂度最大为
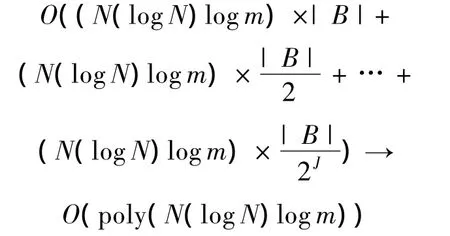
当δ=0时HLSFTS概要数据结构不具有容错能力,对原始数据流进行无容错压缩,图2为无容错HLSFTS结构示意图.
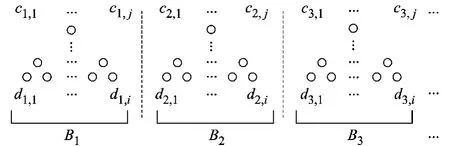
图2 无容错HLSFTS结构图
当概要结构不具有容错特性时,只输出一层提升小波系数,出于简化考虑假设将当前窗口划分为3个批次B1,B2和B3.对B1和B2中的数据进行惰性提升,得到小波系数序列{c1,1,…,c1,l,c2,1,…,c2,l},当窗口滑动,B1中的数据过期而 B3中的数据插入,删除由B1中的数据产生的小波系数序列,对B3中的数据做惰性提升得到新的小波系数序列,与由B2中数据产生的小波系数序列合并输出{c2,1,…,c2,l,c3,1,…,c3,l},完成 HLSFTS 概要数据结构的重构.
2.2 FTGDStream聚类算法
二层聚类框架下的宏观聚类阶段采用基于网格密度的聚类算法更为适合.HLSFTS算法输出小波系数的数据规模很小,在少量小波系数输出的前提下加快了宏观聚类过程中密度网格的划分,算法结构如图3所示.
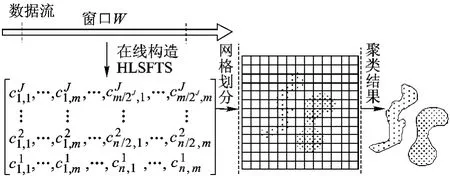
图3 容错网格密度聚类示意图
空间网格的划分是FTGDStream算法的重要过程,基础网格划分定义不同算法的复杂度和聚类结果也不同[7].
定义6 设HLSFTS概要结构随着数据流的流动输出d维提升小波系数C集,将C按维数划分为C=C1×C2×…×Cd,在此基础上进一步对任意维小波系数Ci进行等长划分为Ci=Ci1×Ci2×…×Cip,则整个提升小波系数集C被划分为个单元格.对于任意单元格g存在,其中 ji=1,2,…,pi则 g=(j1,j2,…,jd).
定义7 假设任意时间戳内的任意数据x在时间点tc到达,则其密度是与时间t相关的函数,定义为 D(x,t)= λt-T(x)= λt-tc,其中 λ 称为衰减因子,且 λ∈(0,1).
定义8 对任意空间格g和给定时间t,令E(g,t)为在时间t或之前的空间格g的数据映射,其 密 度 D(g,t)被 定 义 为
定理1 假设单元格g在tl时刻接收数据,在tn时刻接收新数据,并且存在tn>tl,则新的密度计算公式为
证明 令单元格g在tl时刻之前接收的数据为 C={c1,c2,…,cm},根据定义 8 可进一步得到,且根据定义7可得到其中 i=1,2,…,m,因此有
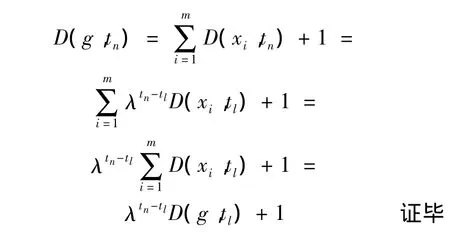
定义9 定义任意空间容错格g的特征向量为三元组(tl,D,L),其中tl为单元格g最后更新数据的时间,D为数据更新后的格密度,L为格的类标签.
定理2 令C(t)为时间戳t内到达的所有数据,则存在
定义11 设存在单元格集合G和任意单元格 g∈G,若 g=(j1,j2,…,jd)在任意维上都有相邻单元格,那么g为单元格集合G的内部单元格,否则g为G的边界单元格.
定义12 令G=(g1,g2,…,gm)是一个单元格集合,若G的每一个内部单元格都是稠密的,每一个边界单元格都是过渡单元格,则称G为单元格聚簇.
定义13 t时刻对于单元格 g存在D(g,t)≥Cm/N(1-λ)=Dm,其中Cm为取值大于1的控制阈值,则称g为稠密单元格.
若在t时刻对于单元格g存在D(g,t)≥ Cl/N(1-λ)=Dl,其中0<Cl<1,则称g为稀疏单元格.
若在t时刻对于单元格 g存在 Cl/N(1-λ)≤D(g,t)≤Cm/N(1-λ),则 g为过渡单元格.
FTGDStream算法采用微观在线聚类和宏观离线聚类的双层聚类技术实现.当窗口滑动时批次内的原始数据做提升小波变换得到第1层小波系数,相邻批次的小波系数做容错度量,对满足容错程度的相邻批次小波系数做提升小波变换生成第2层小波系数,不满足容错条件的小波系数保留在第1层.这一过程反复迭代直至不再存在相邻批次小波系数满足容错条件,生成d维容错小波系数且d≥1.采用倾斜时间框架以快照的形式对在线微观聚类进行保存[8].FTGDStream算法首先对d维小波系数进行单元格划分,然后计算单元格的特征向量,并根据定义划分所有单元格的类型,根据稠密单元格和过渡单元格对整个单元格空间进行聚类,得到最终的聚类簇.以上聚类过程反复执行实现了数据流环境下的容错聚类.
3 实验结果分析与比较
为验证FTGDStream算法的效率,在实验中与HPStream算法和D-Stream算法进行了比较,实验结果如图4~图8所示.实验在主频为3.0 GHz Intel Celeron处理器及512 MB内存的windows XP系统平台下采用Visual C++6.0与Matlab混合编程实现.
实验数据采用UCI数据库中的真实数据集Bag of Word Data Set,US Census Data(1990)Data Set和 Forest Cover Type Data Set.其中 Bag of Word Data Set数据集包含8000000个词汇实例.US Census Data(1990)Data Set数据集为1990年美国人口普查数据集,包含2458285个数据实例和68个属性.Forest Cover Type Data Set数据集来源于美国林务局的资源信息系统数据,数据集中包含581012个数据实例和54个属性值.
首先对FTGDStream算法的聚类准确性进行验证,其中取 Cm=3.0,Cl=0.8,λ =0.998,取数据集54维数据中的44维属性作为实验对象,对多次试验取平均值.图4显示了宏聚类过程中对每一维的数据属性划分长度的不同对聚类正确率的影响,在微观聚类过程中取容错等级为零,FTGDStream算法的平均聚类准确率保持在96%以上.
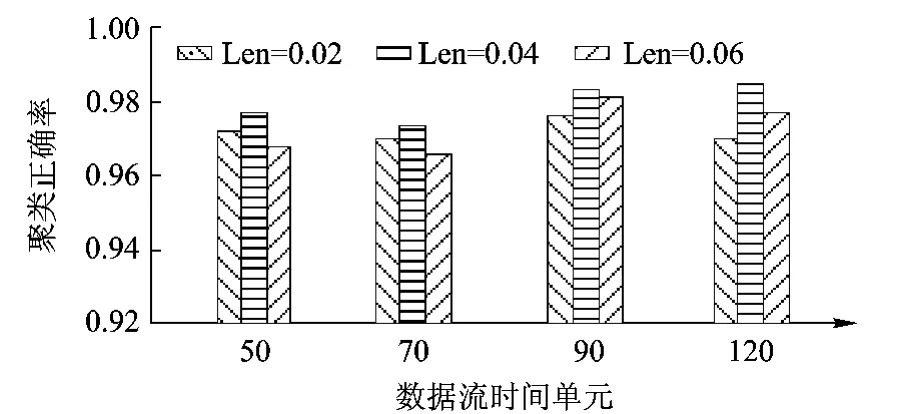
图4 FTGDStream算法聚类准确率
图5显示了微观聚类取不同的容错等级时FT-GDStream算法的最终聚类准确率,划分长度对聚类正确率的影响显著小于容错等级对聚类准确率的影响,容错程度的影响起主导作用.
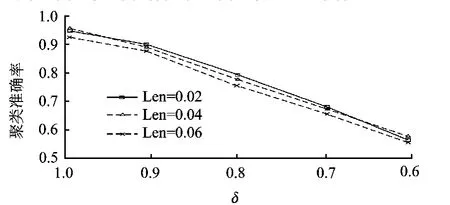
图5 容错水平对聚类准确率的影响
采用Bag of Word Data Set,US Census Data(1990)数据集对FTGDStream算法、HPStream算法和D-Stream算法计算效率进行了比较,数据维数取值10,FTGDStream算法和D-Stream算法的维数划分取值 0.02,取 Cm=3.0,Cl=0.8,λ =0.998.
图6显示FTGDStream算法和D-Stream算法的时间效率约为HPStream算法1/3左右,FTGDStream算法比D-Stream算法的时间效率有略微差距,主要是2种算法的微观聚类阶段运行效率的差异造成的,宏观聚类阶段由于HLSFTS概要结构输出的小波系数远远小于D-Stream算法参加网格划分的数据规模,因此宏观聚类阶段FTGDStream算法的计算效率比D-Stream算法高.

图6 数据规模对算法效率的影响
根据以上分析可以适当的调整HLSFTS概要结构的误差度量准则,使HLSFTS概要结构输出更多的小波系数,提高对原始数据流的重构误差的同时也有助于提高聚类的准确性.
图7显示了当原始数据流的维数发生变化时对FTGDStream算法、HPStream算法和D-Stream算法计算效率的影响,数据维数增加对HPStream算法影响最大.对Bag of Word Data Set数据集进行预处理截取其中1000000个实例,当数据维数增加时HPStream算法计算时间消耗急剧增加,FTGDStream算法与D-Stream算法的时间效率始终相差不多,当维数超过60维时FTGDStream算法的时间效率渐渐超过D-Stream算法,这主要是因为HLSFTS概要结构对高维数据的压缩能力要好于基于网格的划分方法,使得参加宏观聚类的小波系数数量要少于D-Stream算法,因此造成了FTGDStream算法对高维数据的处理能力略好一些,总体看来时间效率差距不大.
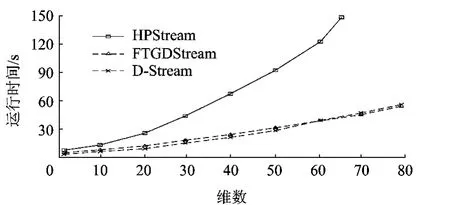
图7 数据维数对算法效率的影响
图8显示了Bag of Word Data Set,US Census Data(1990)Data Set,Forest Cover Type DataSet 3种不同数据规模的数据集对FTGDStream算法时间效率的影响.取3个数据集中的500000个数据实例,其中Bag of Word Data Set数据集取100维属性值,US Census Data(1990)Data Set数据集取68维属性值,Forest Cover Type Data Set数据集取44维属性值.随着不同数据集维数的增加产生相同聚簇数量的时间也随之增加,可以看出数据集的维数对FTGDStream算法的时间效率影响比较大,虽然提升小波变换具有相对较好的多维数据处理性能,当数据量较大且维数较高时算法效率有所下降.
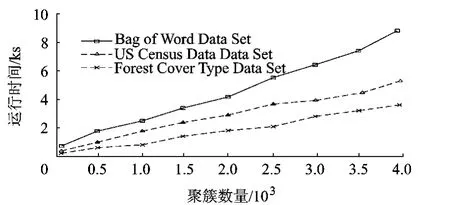
图8 聚簇数量对算法效率的影响
4 结论
本文首先介绍了二层数据流挖掘框架的基本思想,以及将其应用于数据流容错聚类的优势.将二层框架聚类思想与层次小波容错概要数据结构结合在一起,提出一种新的基于二层框架的数据流容错聚类算法,利用容错小波概要数据结构实现在线微观聚类,然后在此基础上对小波容错概要数据结构输出的小波系数进行密度划分,给出了网格的划分方法和基于网格密度聚类的离线宏观聚类算法思想.在UCI数据集上的仿真实验结果表明,FTGDStream算法利用小波概要对原始数据的高压缩率减小网格密度聚类算法的计算负载,增强算法对高维数据的处理能力,进而提高了基于不同容错等级的数据流聚类算法的效率,是一种有效的数据流容错聚类方法
References)
[1]Callaghan O L,Mishra N,Meyerson A.Streaming data algorithms for high-quality clustering[C]//San Jose.Proceedings of International Conference on Data Engineering.California:IEEE Computer Society,2002:685 -699
[2]Chen Y X,Tu L.Density-based clustering for real-time stream data[C]//San Jose.Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.California:ACM,2007:133 -142
[3]Aggarwal C C,Han Jiawei,Wang Jianyong,et al.A framework for clustering evolving data streams[C]//Proceeding of the 29thInternational Conference on Very Large Data Bases.Berlin:Morgan Kaufmann ,2003:81-92
[4]Aggarwal C C,Han Jiawei,Wang Jianyong,et al.A framework for projected clustering of high dimensional data streams[C]//Proceeding of the 29thInternational Conference on Very Large Data Bases.Toronto,Canada:Morgan Kaufmann,2004:852 -863
[5]Chen Mingsheng,Wu Xianliang,Wei Sha,et al.Fast multipole method accelerated by lifting wavelet transform scheme[J].Applied Computational Electromagnetics Society Journal,2009,24(2):109-115
[6]Shahin M,Badawi A,Kamel M.Biometric authentication using fast correlation of near infrared hand vein patterns[J].International Journal of Biometrical Sciences,2007,2(3):141 -148
[7]Cao Feng,Ester M,Qian Weining,et al.Density-based clustering over an evolving data stream with noise[C]//Proceedings of the 6th SIAM International Conference on Data Mining.Bethesda,MD:SIAM,2006:326-337
[8]Han J,Kamber M.Data mining:concepts and techniques[M].2nd ed.Morgan Kaufmann:Elsevier Inc,2006:467 -589
