满足多约束的主动段能量管理制导方法

徐 衡 陈万春

(北京航空航天大学 宇航学院，北京100191)

运载火箭穿越稠密大气过程中，气动力与发动机推力有着强烈的耦合关系，因此主动段制导问题一直都具有很强的挑战性［1］.针对大气层内的主动段制导问题，文献［1－3］通过最优控制方法建立模型，使用经典有限差分法求解两点边值问题，得到满足最优指标的闭环制导规律.然而随着近年来高超音速飞行器的不断发展，高超音速飞行器运载任务对运载火箭制导系统提出了更高的要求，仅仅得到最优制导规律是不够的.

对于高超音速飞行器运载任务，运载火箭制导系统需要满足多种终端约束条件.如高超音速飞行器X-43，在主动段终端要求速度方向沿当地水平方向，即当地弹道倾角为0.对于指定射程弹道，主动段终端速度的大小必须为指定值.为满足分离要求，主动段终端攻角需较小，且分离前需保持定轴飞行，即姿态角变化率为0.同时，在飞行过程中还需要满足动压、动压攻角乘积、过载、姿态角变化率的过程约束条件.上述约束条件对于带关机控制的液体火箭发动机来说比较容易实现，但对于目前广泛使用的耗尽关机型固体火箭发动机来说，则需要通过能量管理来消耗多余能量，以满足上述终端约束条件.

针对固体火箭主动段能量管理问题，各种方法都是通过控制推力与速度之间夹角来消耗多余能量的.

文献［4］和文献［5］提出了一种在主动段初期进行折线式能量管理机动的方法，即设计姿态角为折线式指令来消耗多余能量.然而该方法仅在主动段初期很短的时间内作用，而且离线设计姿态角指令，较为粗糙.其主动段后期制导方法以满足位置和速度方向要求为目标，对于终端速度大小无法控制，因此不能满足高超音速飞行器运载任务的要求.文献［6］在真空飞行假设下提出交变姿态控制能量管理(AEM，Alternate Attitude Control Energy Management)方法.该方法是一种开环制导方法，又是在真空飞行假设下推导得到的，因此不适用于大气层内的主动段制导问题.文献［7］，也是在真空飞行假设下，提出一般能量管理(GEM，General Energy Management)方法.该方法是一种闭环制导方法，真空飞行假设对制导精度影响不大，然而该方法会导致终端攻角以及终端姿态角变化率过大，因此不能满足上述终端约束条件.

本文基于控制推力和速度之间夹角来实现主动段能量管理的思路，综合交变姿态控制能量管理AEM和一般能量管理GEM的优点和适用范围，结合高超音速飞行器运载任务的制导约束条件，提出了样条能量管理(SEM，Spline Energy Management)制导方法，并针对分离前定轴飞行约束条件进行了修正.以三级运载火箭为例进行仿真，通过AEM，GEM和SEM对比，验证了样条能量管理制导方法的可行性.

1 主动段模型及能量管理制导方法

1.1 数学模型

在速度坐标系下建立运载火箭主动段质心动力学方程如下:

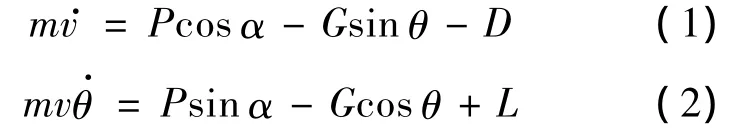
其中，m为质量;v为速度;α为攻角;θ为弹道倾角;P为推力;G为重力;D为阻力;L为升力.

在发射坐标系下建立运载火箭主动段质心运动学方程如下:

其中，x为发射坐标系横轴坐标;y为发射坐标系纵轴坐标.

1.2 能量管理制导方法基本原理

为阐述主动段能量管理制导方法的基本原理，首先在俯仰平面内引入坐标系见图1.某一时刻的速度矢量为V，其与x轴的夹角Θ为当地弹道倾角.根据主动段结束时当地弹道倾角为0的终端约束条件，期望速度矢量VD沿x轴，其大小为指定值vD.由此可得到需用速度增益矢量为

其中，ΔV的大小为Δv，即需用速度增益.一般来说，需用速度增益比可用速度增益要小.简单起见，在只考虑发动机推力对飞行器的加速能力时，可用速度增益VCAP可由式(6)估算:

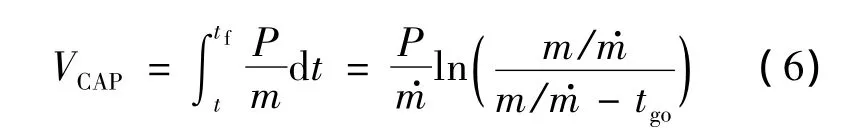
其中，t为当前时刻;tf为主动段结束时刻;tgo为剩余飞行时间;m·为质量秒流量，取正值.

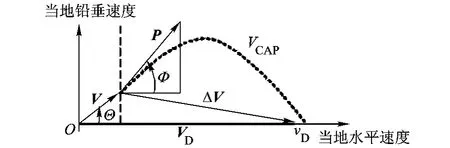
图1 能量管理基本原理图

得到ΔV和VCAP后，主动段能量管理制导方法的基本原理是设计如图1虚线所示的VCAP曲线，使其通过ΔV的起点和终点，并且曲线长度为VCAP，进而控制发动机推力矢量P与曲线相切，即通过俯仰角φ控制当地俯仰角Φ，使速度矢量V跟踪该曲线最终达到期望速度矢量VD.

1.3 样条能量管理SEM

在Zarchan提出的一般能量管理GEM中，VCAP曲线被设计成圆弧形状，但会产生较大的终端攻角，不能满足终端约束条件.为满足终端攻角较小的约束条件，VCAP曲线可以设计成样条曲线形状，如图2所示，因此将这种方法称为样条能量管理SEM.

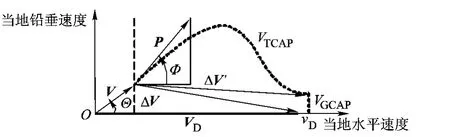
图2 样条能量管理SEM

在图2中，可用速度增益VCAP被分为由发动机推力产生的可用速度增益VTCAP和由重力产生的可用速度增益VGCAP.在进行能量管理的高度，相比发动机推力和重力，空气动力对可用速度增益的贡献可以忽略不计.因此，可用速度增益VCAP可以表示为

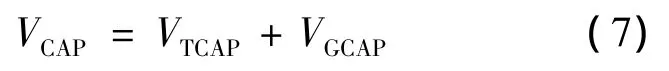
考虑当地水平方向相对初始水平方向的转动效应，VGCAP可以表示如下:

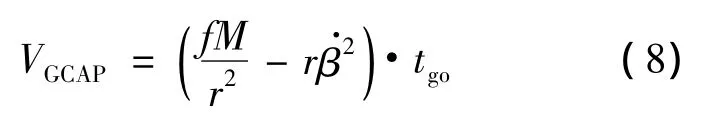
其中，fM为3.986005×1014;r为火箭质心到地心的距离;β·为射程角变化率.由于重力始终与当地水平方向垂直，因此VGCAP曲线为垂直于x轴的直线，曲线长度为VGCAP，如图2所示.

VTCAP可以由式(6)得到:

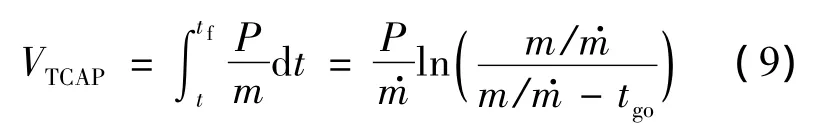
由图2可知，VTCAP曲线为样条曲线，则其表达式为三次多项式:

其中 A，B，C，D 为 f(x)的待定系数.将式(10)左右两端对x求导可以得到:

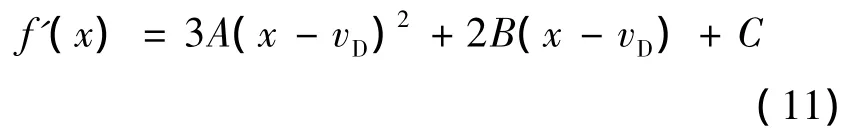
为确定f(x)的待定系数，考虑如下条件.如图 2 所示，VTCAP曲线的起点为(vcos Θ，vsin Θ)，终点为(vD，VGCAP)，曲线长度为VTCAP，连接起点和终点的矢量为ΔV′，其大小为Δv′.由终端约束条件可知，终端攻角αf要趋近于0，αf可以表示为

其中终端当地弹道倾角Θf为0，则终端当地俯仰角Θf要趋近于0.由式(9)可知，VTCAP为发动机推力全部用于加速而产生的可用速度增益，则发动机推力矢量P显然与VTCAP曲线相切，即

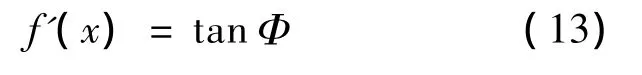
因此，f′(x)在终端处要求为0.由此可以得到求解f(x)4个待定系数的4个条件方程如下:

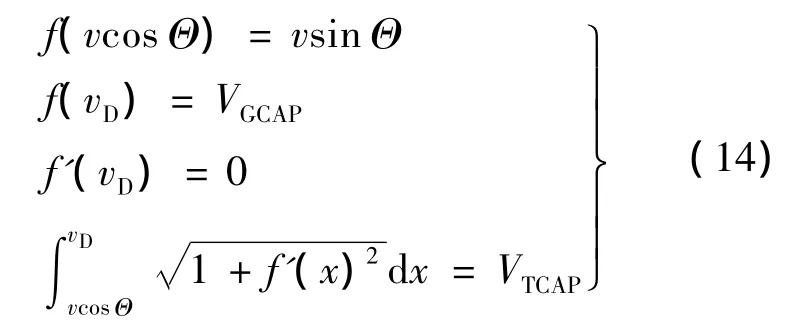
得到VTCAP曲线f(x)后，建立指令俯仰角模型见图3.为保证速度矢量V跟踪VTCAP曲线，在给定的当地水平速度下，将当地铅垂速度与f(x)的偏差ΔvV，以及当地俯仰角Φ与f′(x)反正切的偏差ΔΦ作为反馈控制偏差量，则由图3可得

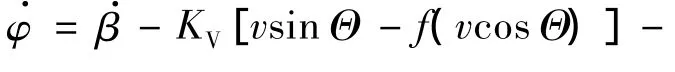
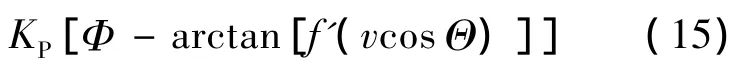
其中KV和KP为偏差量比例系数.为保证飞行过程中俯仰角变化率幅值小于10(°)/s的约束条件，将φ·限幅后进行积分得到指令俯仰角φ，使速度矢量V跟踪VTCAP曲线，最终达到期望速度矢量VD.在仿真过程中，VTCAP曲线实时更新.为保证式(14)有解，如图2所示，要求 VTCAP始终比 Δv′大，因此当 VTCAP接近 Δv′时，VTCAP曲线停止更新，并生成新的样条曲线将速度矢量直接导向期望速度矢量，而不是导向点(vD，VGCAP).

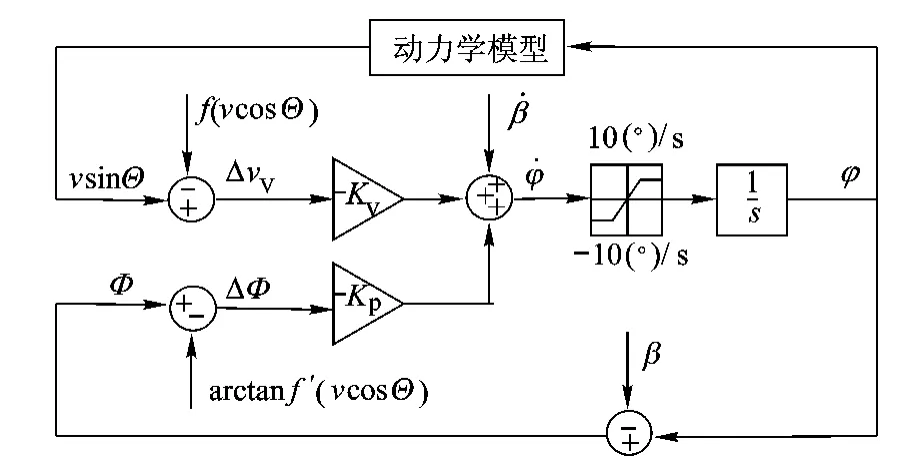
图3 指令俯仰角模型

1.4 分离前定轴飞行修正

为了满足终端分离前定轴飞行的约束条件，在终端分离前tS内，将样条曲线设计成沿横轴的直线，如图4所示，同时考虑重力在终端分离前tS内对速度的影响，将终端分离前tS时刻的期望速度设定为(vDS，VGCAPS).图4中VGCAPS为tS内重力产生的可用速度增益，VTCAPS为tS内发动机推力产生的可用速度增益，VTCAPR为终端分离前tS之前发动机推力产生的可用速度增益，显然

其中，vDS为终端分离前tS时刻的当地水平期望速度，由图4可知

如图4所示，在终端分离前tS之前，忽略终端分离前tS之前重力产生的可用速度增益，以(vDS，VGCAPS)为终点对VTCAPR曲线进行样条能量管理，终端分离前tS内，将VTCAPS曲线设计成沿横轴的直线以满足终端分离前定轴飞行的约束条件，同时满足终端速度为指定值，终端当地弹道倾角为0，终端攻角较小的终端约束条件.

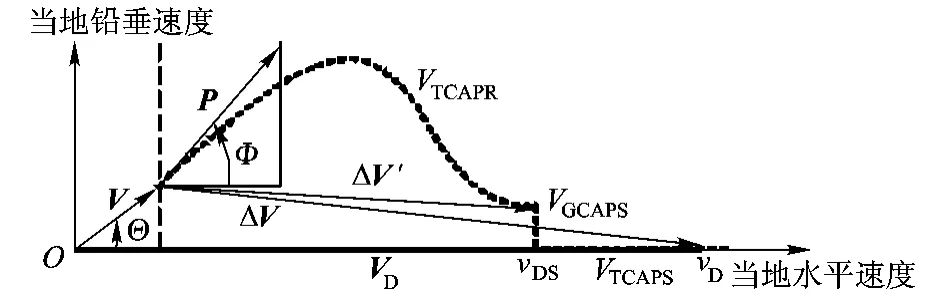
图4 满足分离前定轴飞行的样条能量管理

2 SEM制导方法仿真结果

本文以三级运载火箭为例研究运载火箭主动段制导问题.首先根据主动段数学模型，优化得到符合过程约束和终端约束的主动段最大终端速度弹道.运载火箭第1，2级按照最大终端速度弹道飞行，第3级采用样条能量管理SEM制导方法飞行，以满足各项终端约束条件.

设定期望速度为6000 m/s，在第3级开始阶段，终端分离前tS之前，通过实时更新计算得出VTCAP曲线，速度曲线则跟踪VTCAP曲线，如图5所示.在图6 中，当 VTCAP接近 Δv′时，VTCAP曲线停止更新，并生成一条新的样条曲线将速度矢量直接导向终端分离前tS时刻的期望速度，如图5所示.样条曲线系数更新变化如图7所示，12.6 s后样条曲线系数均为常值，即VTCAP曲线停止更新，新的样条曲线系数不再变化.终端分离前tS内，VTCAP曲线为沿当地水平速度方向的直线，如图5所示，样条曲线系数均为0，如图7所示.

图5 样条能量管理(SEM)仿真结果

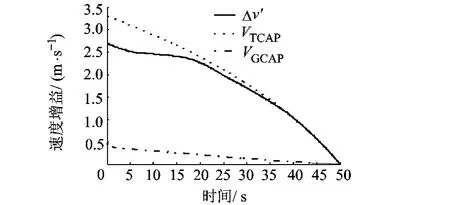
图6 第3级速度增益曲线

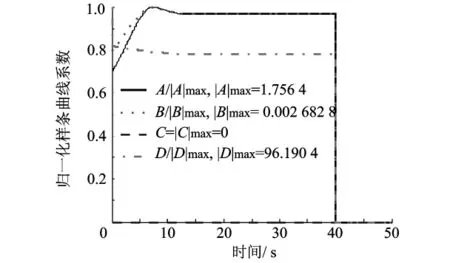
图7 归一化样条曲线系数

仿真结果同时还满足动压、动压攻角乘积、横向过载以及俯仰角变化率的过程约束条件，见图8.主动段指令俯仰角和弹道见图9、图10.最终，如图11～图14所示，终端速度为6000.0 m/s，终端当地弹道倾角为0.029 287(°)，终端攻角为3.1712(°)，终端分离前5 s俯仰角变化率为0，满足各项终端约束条件。

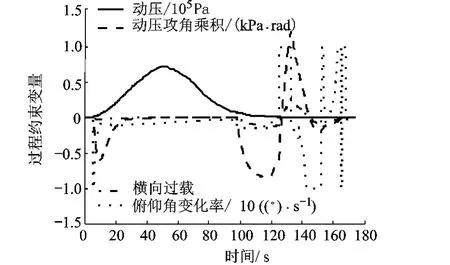
图8 过程约束变量曲线

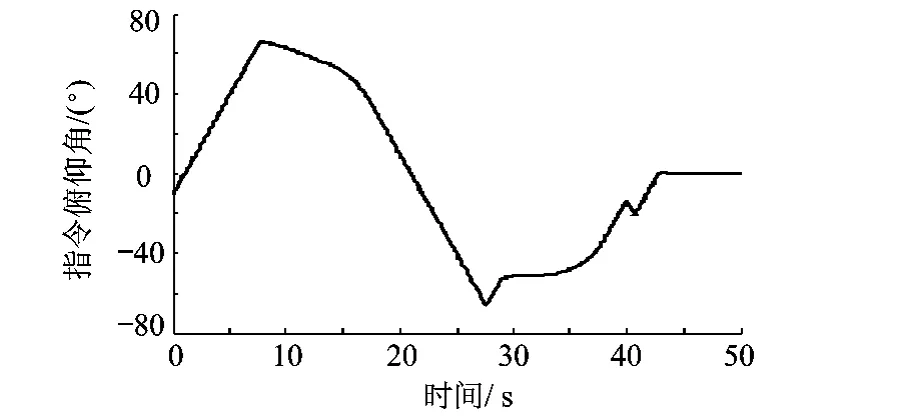
图9 第3级指令俯仰角曲线

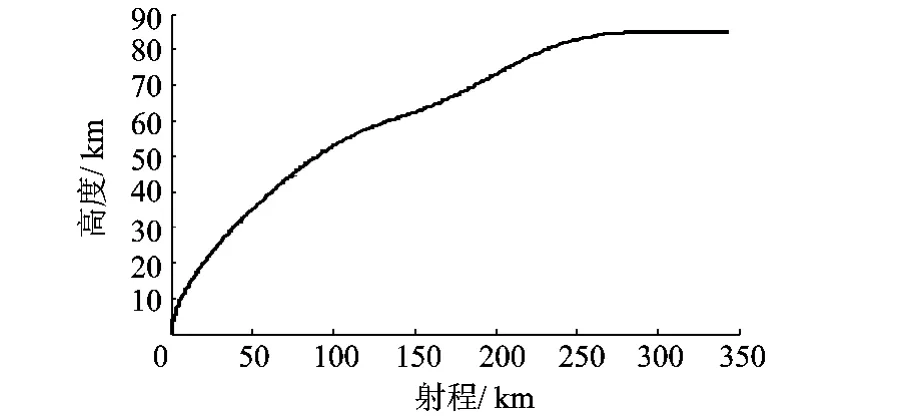
图10 主动段弹道

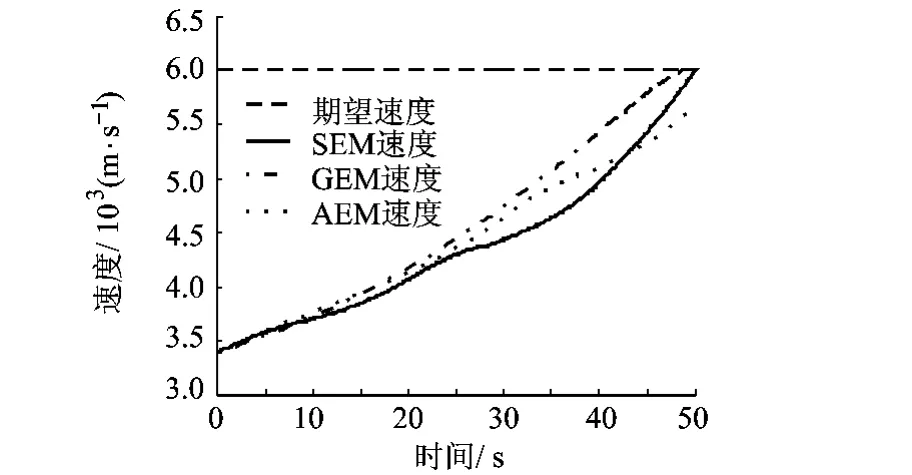
图11 第3级速度曲线

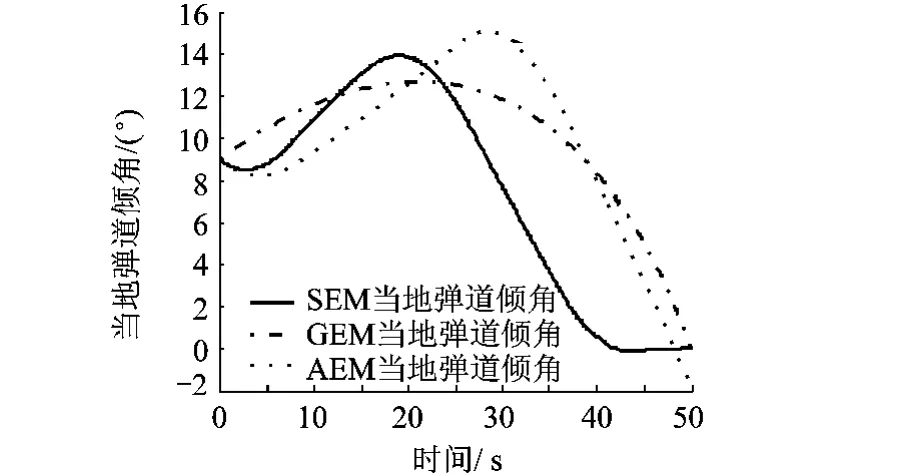
图12 第3级当地弹道倾角曲线

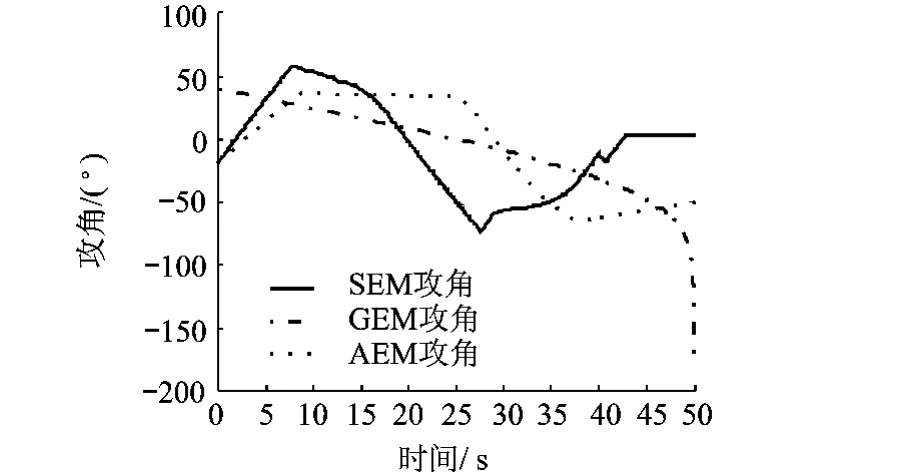
图13 第3级攻角曲线

图14 第3级俯仰角变化率曲线

3 AEM，GEM和SEM对比分析

针对与主动段终端约束相关的速度、当地弹道倾角、攻角以及俯仰角变化率，对 AEM，GEM和SEM进行对比，如图11～图14所示.由图11可以看出，GEM和SEM的速度曲线最终都能达到期望速度值，而AEM是基于真空飞行假设的开环制导方法，真空飞行假设引入的误差不能在闭环内修正，导致AEM速度曲线偏离期望速度.同样的，在图12中GEM和SEM的当地弹道倾角曲线最终都收敛到0，而AEM的终端当地弹道倾角与0还有一定的偏差.GEM方法虽然满足速度和当地弹道倾角的终端约束，但在图13中可以看出，GEM的终端攻角非常大，且如图14所示，GEM的终端分离前俯仰角变化率也非常大.通过对比分析可以看出，闭环方法GEM和SEM相比开环方法AEM在制导精度上有明显的优势，SEM相比GEM在满足制导精度的同时还能够较好的满足终端攻角约束条件以及俯仰角变化率约束条件.因此，样条能量管理SEM能够满足主动段各项约束条件，为运载火箭主动段制导提供了一种新的方法.

4 结论

1)提出了一种新的样条能量管理SEM运载火箭主动段制导方法，并针对分离前定轴飞行约束条件进行了修正.通过三级运载火箭仿真结果，验证了该方法的可行性.

2)通过AEM，GEM和SEM的对比分析，明确了样条能量管理SEM制导方法的优越性，为高超音速飞行器运载任务主动段制导提供了一种新的方法.

3)研究过程中主要考虑了主动段制导的终端约束条件，对于过程约束条件仅考虑了动压、动压攻角乘积、横向过载以及俯仰角变化率的约束，其他过程约束对样条能量管理SEM制导方法的限制和影响有待进一步研究以完善该方法。

References)

［1］Lu Ping，Sun Hongsheng，Tsai B.Closed-loop endoatmospheric ascent guidance［J］.Journal of Guidance，Control，and Dynamics，2003，26(2):283 －294

［2］Lu Ping，Pan Binfeng.Highly constrained optimal launch ascent guidance ［J］.Journal of Guidance，Control，and Dynamics，2010，33(2):404 －414

［3］Dukeman G A.Atmospheric ascent guidance for rocket-powered launch vehicles［R］.AIAA-2002-4559，2002

［4］Kuroda T，Imado F.A mid-course guidance law for highly maneuverable thrust vector control missiles［R］.AIAA-97-3688，1997

［5］关为群，殷兴良.美国THAAD导弹能量管理控制机动研究［J］.现代防御技术，2005，33(3):43 －47 Guan Weiqun，Yin Xingliang.Study on energy management steering maneuver of American THAAD interceptor［J］.Modern Defence Technology，2005，33(3):43 －47(in Chinese)

［6］贾沛然，陈克俊，何力.远程火箭弹道学［M］.长沙:国防科技大学出版社，1993:235－241 Jia Peiran，Chen Kejun，He Li.Ballistic for long-range rocket［M］.Changsha:National University of Defence Technology Press，1993:235 －241(in Chinese)

［7］Zarchan P.Tactical and strategic missile guidance［M］.3rd ed.Virginia:AIAA，1997:281－290

［8］Muse J A，Calise A J.Limited adaptive authority flight control for the crew launch vehicle［R］.AIAA-2009-5960，2009

［9］Pan Binfeng，Lu Ping.Improvements to optimal launch ascent guidance［R］.AIAA-2010-8174，2010

［10］佘智勇，马广富，沈作军.基于间接伴随法的大气层内高超音速飞行器最优上升轨迹研究［J］.宇航学报，2010，31(8):1951－1957 She Zhiyong，Ma Guangfu，Shen Zuojun.Indirect adjoint method-based endoatmospheric ascent trajectory optimization for hypersonic vehicle［J］.Journal of Astronautics，2010，31(8):1951－1957(in Chinese)

［11］杨希祥，江振宇，张为华.小型运载火箭大气层飞行段飞行程序设计研究［J］.飞行力学，2010，28(4):68 －72 Yang Xixiang，Jiang Zhenyu，Zhang Weihua.Flight program design for small launch vehicle in atmosphere flight stage［J］.Flight Dynamics，2010，28(4):68 －72(in Chinese)