基于反演设计的机器人非奇异终端模糊滑模控制
2012-12-14徐传忠王永初
徐传忠,王永初
(1.华侨大学信息学院,福建 厦门 361021;2.华侨大学 机电学院,福建 厦门 361021)
0 引言
滑模变结构控制(Sliding Mode Variable Structure Control,SMVSC)对有外界干扰和模型误差具有较好的鲁棒性,在不确定非线性系统的控制中得到广泛的应用[1,2]。反演(backstepping)设计方法对带有参数严格反馈形式的非线性系统,提供了递推的步骤从而保证了系统的全局稳定性[3]。终端滑模(terminal sliding mode,TSM)控制使控制系统具有有限时间收敛的优点[4],但是系统状态接近零时,控制律中状态负指数项会导致控制量趋向于无穷大,产生奇异点[5],为此文献[6]设计了非奇异终端滑模控制。本文在此基础上设计了反演非奇异终端模糊滑模控制。该方法根据滑模控制原理,采用反演设计方法,为了削弱抖振设计了模糊控制器对建模误差和干扰的自动跟踪,并且利用李亚普诺夫定理证明了系统的稳定性。
1 系统描述
对于具有n个旋转关节的刚性机器人,其动态性能可由以下二阶非线性微分方程描述[3]:

其中:
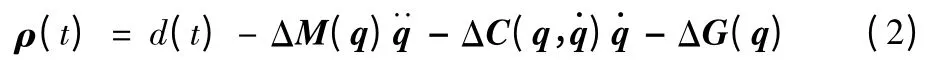
2 反演非奇异终端模糊滑模控制器
2.1 反演非奇异终端滑模控制
定义x1=q,x2=,则系统(1)可改写为:
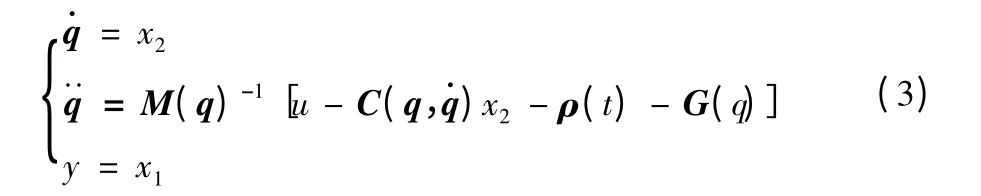
定义关节位置跟踪偏差为:

其中yd为期望角度,且yd具有二阶导数。两边求导可得:
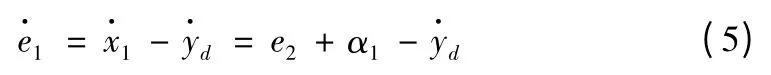
实际速度和它的理想速度的偏差为:

其中:
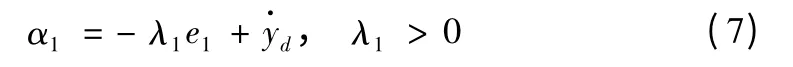
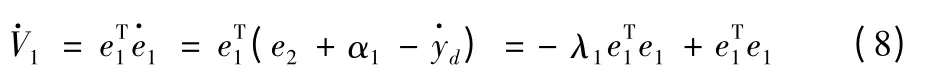
对式(6)求导得:

定义非奇异终端滑模面为:

其中,c1>0为常数,γ,β为奇数,且满足
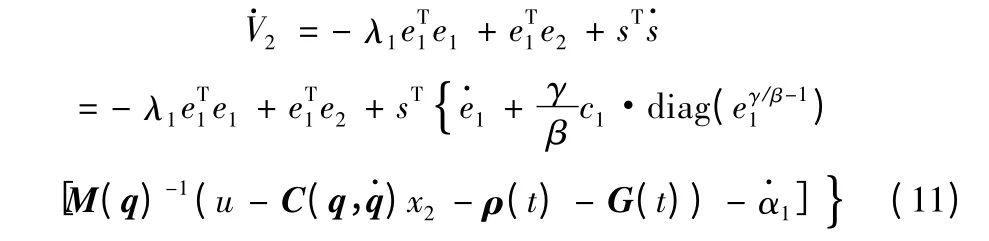
根据式(11),反演滑模控制律可以设计为:

其中:
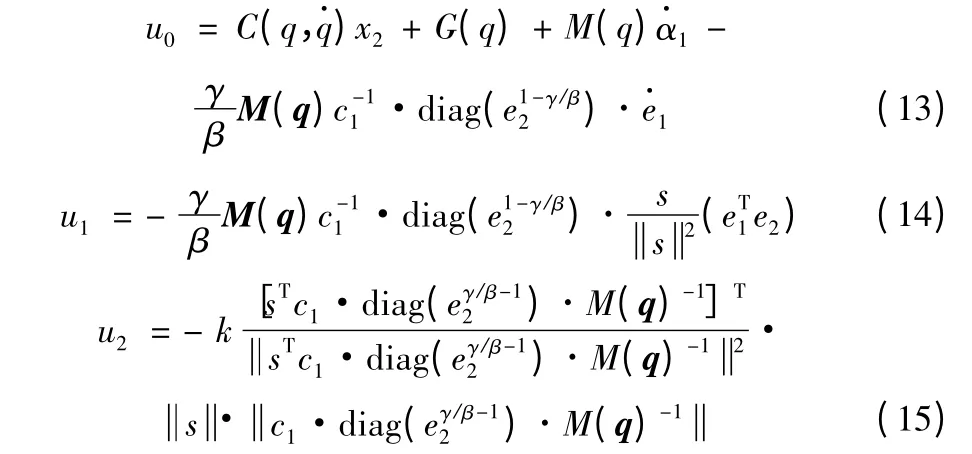
2.2 模糊控制器
为降低模糊控制器的复杂性,采用一个关节一个模糊控制器的方法。根据滑模到达条件设计模糊控制规则。模糊系统的输入输出隶属度函数采用高斯函数,模糊规则如表1所示,其中{PB、PM、PS、ZO、NS、NM 、NB}分别表示{正大、正中、正小、零、负小、负中、负大}。模糊控制器的输入ss·的论域取为[-10,10],输出的论域为[-1,1]。

表1 模糊控制规则
2.3 稳定性分析
两边求导可得:
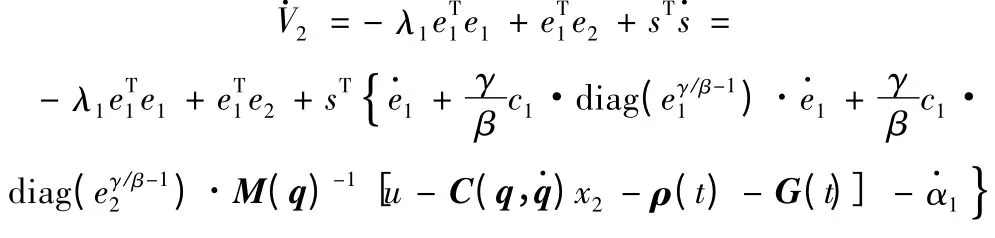
将式(12)代人上式得:

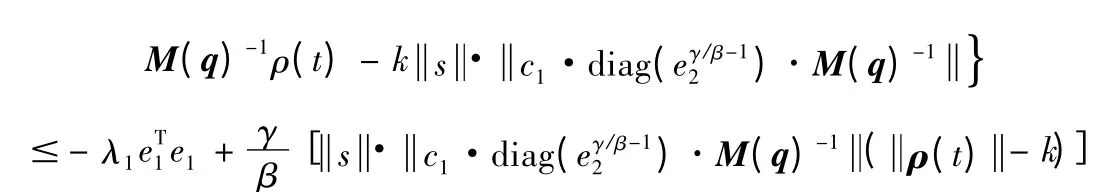
3 仿真分析
二关节机器人系统的动力学模型为:
期望轨迹为:r1=sin(πt)和 r2=cos(πt);系统初始状态为[q1,,q2,]=[0.5,0,0.5,0]。
仿真结果如图1和图2所示,图1和图2分别显示反演非奇异终端滑模控制和反演非奇异终端模糊滑模控制两种方法的仿真结果。其中r1(t)、q1(t)和u1(t)分别代表了关节1的期望角位移运行轨迹、实际角位移运行轨迹和控制输入;r2(t)、q2(t)和u2(t)分别代表了关节2的期望角位移运行轨迹、实际角位移运行轨迹和控制输入。仿真结果表明两种控制方法都能有效地跟踪指令信号。在控制器抖动上,u1(t)和u2(t)表明模糊滑模控制器的抖动明显比滑模控制器的要小。
4 结束语
本文对含有外界干扰和模型误差的多关节机器人系统,设计了反演非奇异终端模糊滑模控制,并构造李亚普诺夫函数,证明了控制系统的稳定性。设计了模糊控制器在线估计不确定性上界值,自动跟踪建模误差和干扰,削弱了抖振。仿真实验表明所提出方法的有效性和可行性。
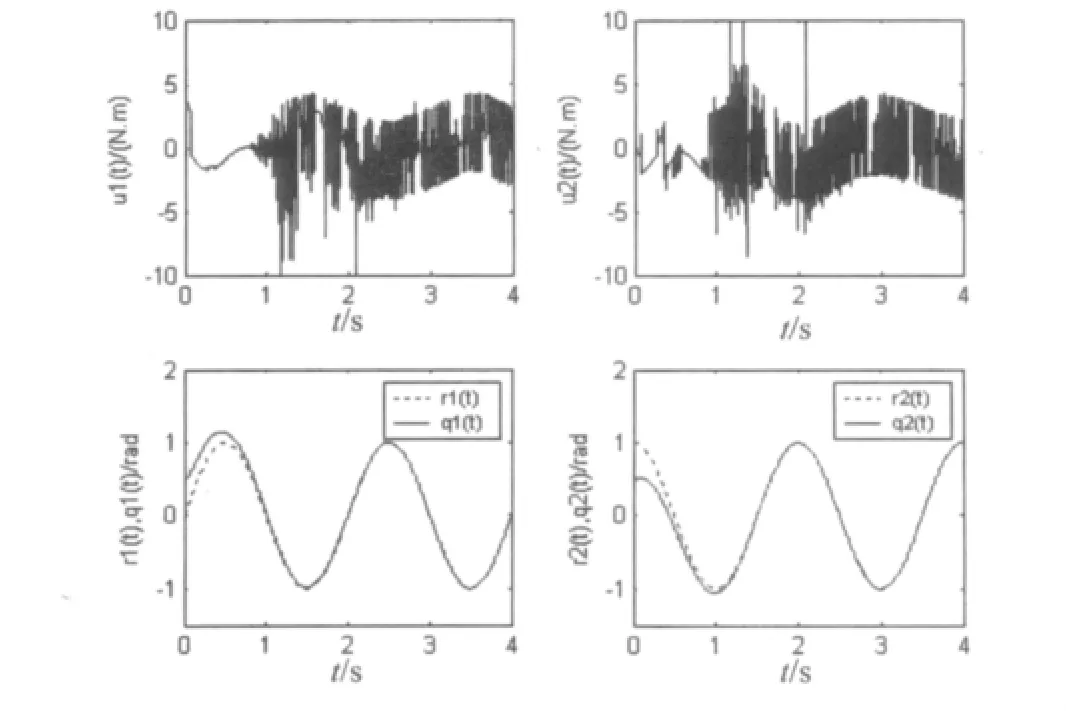
图1 非奇异终端滑模控制
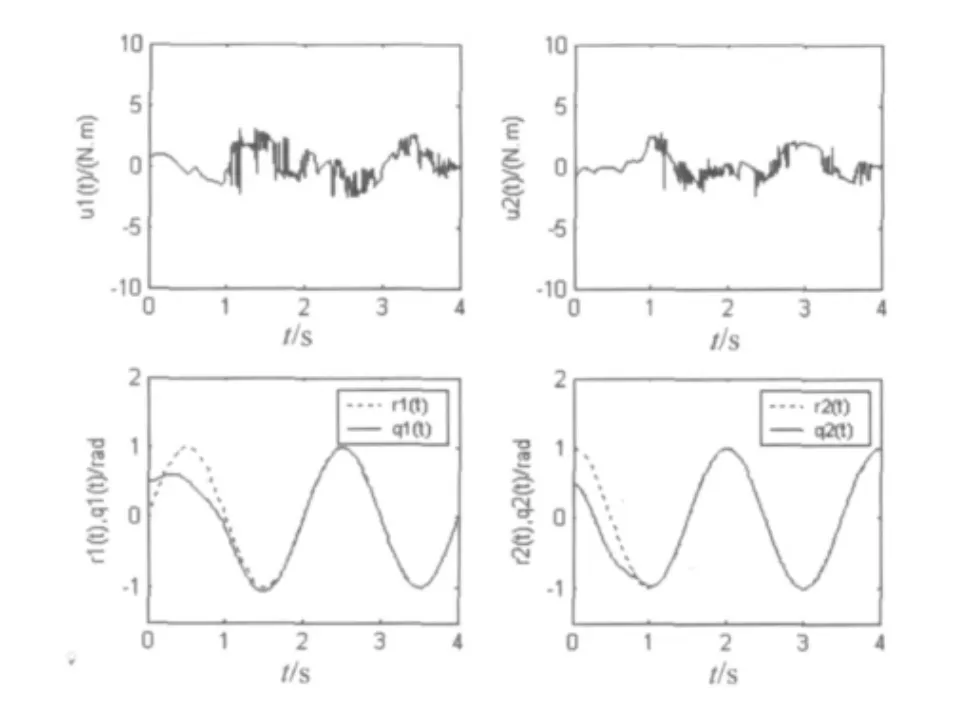
图2 非奇异终端模糊滑模控制
[1]F J Lin,P H Shen.Adaptive backstepping sliding mode control for linear induction motor drive [J].Electric Power Applications,IEEE Proceedings,2002,149(3):183 -193.
[2]Chi-Ying Liang,Juhng-Perng Su.Anew approach to the design of a Fuzzy sliding mode controller[J].Fuzzy Sets and Systems.2003,139(2):111-124.
[3]陈卫东,唐得志,王海涛,等.基于 Backstepping的机器人鲁棒跟踪控制[J].系统仿真学报.2004,16(4):837 -838.
[4]Venkataraman S T,Gulati S.Terminal sliding modes:A new approch to nonlinear control synthesis[A].Proceeding of the International Conference on Advanced Roboties[C].Piscataway,NJ,USA:IEEE,1991.443 -448.
[5]Man Z H,Yu X H.Terminal sliding mode control of MIMO linear systems[A].Proceedings of the IEEE Conference on Decision and Control[C].Piscataway,NJ,USA:IEEE,1996.4619 -4624.
[6]Lin C K.Nonsingular terminal sliding mode control of robot manipulators using fuzzy wavelet networks[J].IEEE Transactions on FuzzySystems,2006,14(6):849-859.
