风力发电机单神经元内模解耦研究
2012-12-14李雪龙周渊深
李雪龙,周渊深
(1.中国矿业大学 信息与电气工程学院,江苏 徐州 221008;2.淮海工学院 电子工程学院,江苏 连云港 222005)
0 引言
风力发电机基于磁场定向的矢量变换控制技术实现了转子电流M轴分量和T轴分量的静态解耦,但变换后仍然存在M轴和T轴间的交叉耦合电压,要想获得高精度的控制性能,有必要对其进行解耦。
内模控制由于其设计简单、控制性能良好以及所蕴含的解耦机制,在工业过程控制尤其是在具有耦合的多变量系统中获得广泛应用。但是内模控制却依赖于对象的逆模型,使其在应用上受到了一定的限制。风力发电机的数学模型为多变量、非线性、强耦合模型,因此获得风力发电机的逆模型难度比较大。近年来,人工神经网络已逐步应用于电机控制系统中,神经网络的算法复杂且收敛速度慢是一直未被克服的难题。单神经元由于其算法简单且具有自适应能力而被广泛应用于电机控制领域中。本文将内模控制与单神经元结合,通过泰勒级数展开将内模控制器约化为具有PID结构的控制器,因为PID控制具有一定的鲁棒性,且又结合了神经元使其不过分依赖于风力发电机的数学模型,仿真表明该种方案几乎可以实现被控对象的彻底解耦。
1 DFIG的数学模型
当DFIG的定、转子均按电动机惯例建模时,同步旋转M-T坐标系下的DFIG数学模型如下:
定子电压方程:

转子电压方程:

定子磁链方程:
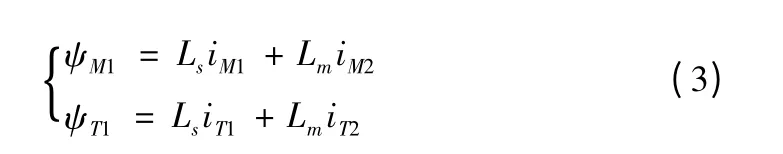
转子磁链方程:

其中:Rs、Rr为定、转子电阻;Ls、Lr、Lm为定、转子自感和定、转子间的互感;uM1、uT1、uM2、uT2为定、转子电压的 M、T 轴分量;iM1、iT1、iM2、iT2为定、转子电流的 M、T 轴分量;ψM1、ψT1、ψM2、ψT2为定、转子磁链的 M、T轴分量;ωs、Δω为旋转磁场同步角频率和转差角频率。
DFIG 空载并网时,iM1=0,iT1=0,代入式(3)、(4)可得:

风力发电系统中的DFIG的定子与电网相连,由于电网电压较高,定子电阻压降与定子反电势、互感压降相比可以忽略。将式(6)代入式(2)可得DFIG空载并网时的转子数学模型:
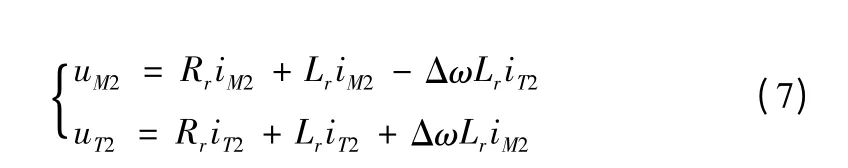
由(7)式可知转子M轴和T轴电压相互耦合,且大小为 ΔωLriT2、ΔωLriM2方向相反。
2 DFIG单神经元内模解耦控制原理
2.1 单神经元内模解耦原理
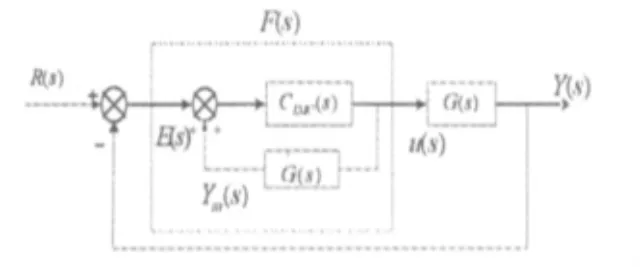
图1 内模控制等效反馈控制结构图

根据系统的实际情况,由(7)式可得电机转子的传递函数模型如下:

根据内模控制原理有内模控制器:

其中L(s)为滤波器,由于DFIG的转子传递函数无有半平面零点和滞后环节则滤波器可取为:
L(s)=λ/λ+si,由图1可得系统输入输出关系为:
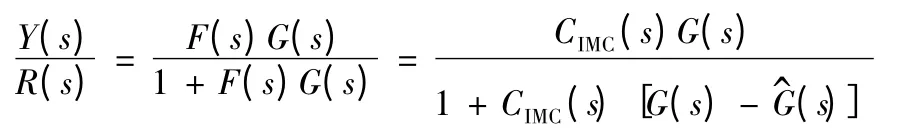
当被控对象与模型完全匹配,内模控制器中包含了模型的逆,因此适当选择L(s)为对角结构即可实现解耦。当保留内模控制结构而结合单神经元时也保留了内模控制本身所蕴含的解耦功能。
将上述结果带入到(8)式中,并设:
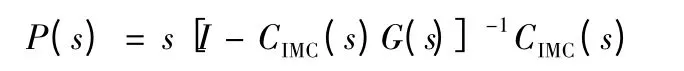
则F(s)=s-1P(s)。将P(s)在s=0处泰勒级数展开得:

其中P、I、D分别为等效PID控制器的比例积分微分系数,R(s)为误差项。由于单神经元结构简单且具有参数自适应性。将其合理的结合到内模控制中使控制器既具有内模控制的解耦功能,又具有神经元的参数自适应性来拓宽控制器的适用范围。因此将(9)式中的P、I、D用神经元控制器代替,将文献[4]中的内模控制器用神经元控制器代替,得到如图2所示的风力发电机中具体的神经元内模控制器结构框图。和分别为转子电流的给定值,iM2和iT2分别为转子实际电流。SNC1-SNC4为单神经元控制器,由内模控制原理可知SNC1与SNC4应有相同的结构,具有一样的增益系数,SNC2与SNC3具有相同的结构并且SNC2和SNC3起到主要的解耦作用,通过调节两者的系数可以调节解耦的强弱。

图2 单神经元内模控制器结构框图
2.2 单神经元PID的算法与实现
单神经元自适应控制器是通过加权系数的调整来实现自适应、自组织功能的,权系数的调整是按有监督的Hebb学习规则实现的。学习算法为:

式中:

ηP,ηI,ηD分为比例、积分、微分的学习速率,K为神经元的比例系数,K >0。
对积分I、比例P和微分D分别采用了不同的学习速率 ηP,ηI,ηD,以便对不同的权系数分别进行调整。K值的选择非常重要,K越大,则快速性越好,但超调量大,甚至可能使系统不稳定。当被控对象时延增大时,K值必须减少,以保证系统稳定。K值选择过小,会使系统的快速性变差。
由于单神经元的算法并不能用传递函数来实现,因此本文用可读性好、易于编写的MATLAB中的S函数实现神经元控制器的功能。以下是完整的算法程序:




3 仿真分析
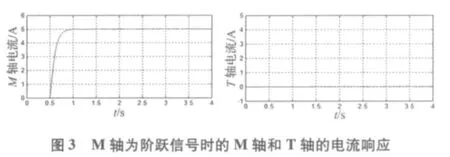
设转子电阻 Rr=1.62 Ω 和转子电感 Lr=4.5 mH,经计算得ΔωLr=1.42。当M轴电流为阶跃信号,T轴电流信号为零时的波形如图3;当T轴电流为阶跃信号,M轴电流信号为零时的波形如图4;当M轴和T轴同时为阶跃信号但跳跃时刻不同时的波形如图5。从图3和图4可以看出:当参数调整好以后,若仅M轴或T轴有信号时,由系统响应的波形图可知,另一条通道几乎不受影响,即实现了双变量系统的解耦,且解耦效果良好。而当M轴和T轴都存在阶跃信号时,但阶跃时刻不同,由系统响应波形图可以看出两个通道的响应相互独立不受影响,即在该种情形下也实现了系统的解耦。
4 结束语
本文介绍了神经元内模控制器的原理,并给出了MATLAB仿真实现,将其应用于风力发电机的转子电流环中。通过仿真结果分析证明了这种实现形式的可行性,在仿真调试过程中还表明除比例增益系数K外,其它参数都可以在较大范围内取值而对系统的性能不产生显著影响。这也是该控制器的优点,在实际应用中可通过现场实验来确定K的大小。并且由于具有算法简单、实时性强、动态响应速度较快,具有一定的工业实用价值。根据对象的运行参数将中间两个起主要解耦作用的控制器的系数制成表在对象运行时根据运行工况调用,将会获得更好的动态解耦效果。
[1]马小亮.大功率交交变频调速及矢量控制技术[M].北京:机械工业出版社,2004.
[2]Garcia C E,Morari M.Internal model control of an unifying review and some new results[J].Ind Eng Chen Pro Des Dev,1982,21(3):308 -323.
[3]周渊深,朱希荣.风力发电机转子电流交叉耦合电压的多自由度内模解耦研究,中国控制与决策学术年会论文集[C].辽宁:东北大学出版社,2010.
[4]李明,林永君.自适应神经元非模型多变量系统解耦控制[J].计算机仿真,2003,20(3):68 -71.
[5]刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003.
