一种改进的异步电机无速度传感器的直接转矩控制系统
2012-12-14李鸿彪曼苏乐
李鸿彪,曼苏乐
(上海交通大学 电气工程系 电力传输与功率变换控制教育部重点实验室,上海 200240)
0 引言
直接转矩控制DTC(Direct Torque Control)是矢量控制后出现的一种新型的高性能交流调速传动控制技术,由德国学者M.Depenbrock和日本学者 I.Takahashi在20世纪80年代首先提出[1,2]。DTC控制思想新颖,控制结构简单,控制手段直接,信号处理的物理概念明确,转矩响应迅速,是一种具有高静、动态性能的交流调速方法[3,4]。在高性能的DTC中,转速的闭环控制环节一般是必不可少的。通常采用光电编码器等速度传感器来进行转速检测,但速度传感器的使用增加了系统的安装难度及成本。本文用一种新的磁链观测方案观测定子磁链[5],并将其作为参考模型,构成新的模型参考自适应系统MRAS(Model Reference A-daptive System),可以在全速度范围内准确辨识速度,同时用模糊速度调节器代替传统PI调节器[6],进一步改善了直接转矩控制在全速范围内的性能,尤其是极低速的性能。
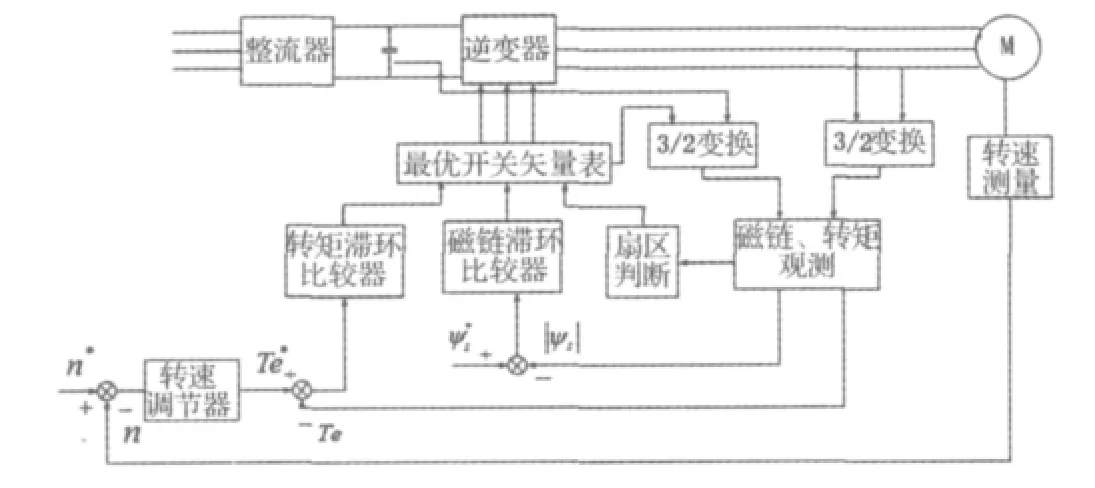
图1 直接转矩控制结构图
1 异步电动机磁链和速度的辨识
三相异步电机在旋转坐标系下的数学模型[7]:电压方程:
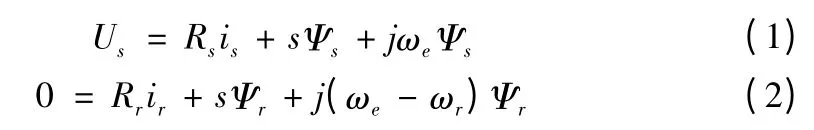
磁链方程:

电磁转矩方程:

运动方程:

符号说明:Rs定子电阻;Rr转子电阻;Ls定子电感;Lr转子电感;Lm定、转子互感;Ψs定子磁链矢量;Ψr转子磁链矢量;is定子电流矢量;ir转子电流矢量;Te电磁转矩;TL负载转矩;p极对数;J转动惯量;ωr转子转速;ωe旋转坐标系dq轴的旋转速度;τr转子时间常数;s微分因子;下标加 d,q表示各变量在 d,q轴上的分量,上标加e表示此变量在旋转坐标系中。
由(2)、(4)得在旋转坐标系下的转子磁链方程为:

方程(7)即转子磁链估计的电流方程,当电机在低转速时,此方程磁链估计准确。当ωe=ωr时,Ψr在d,q轴上的分量为:
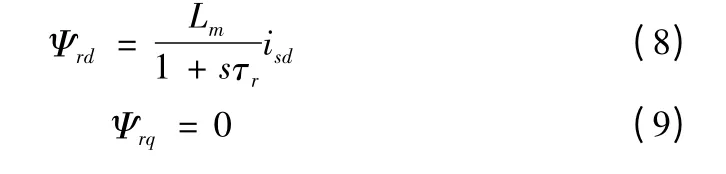
所以将电流方程得到的转子磁链带入方程(3)、(4)得到定子磁链为:

由方程(1)得基于电压方程的定子磁链为:
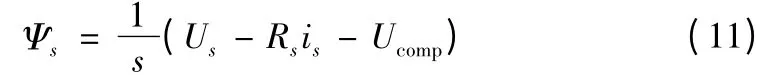
新的磁链辨识方法在传统的电压模型基础上加入了一个电压补偿Ucomp,以补偿由于电压模型的纯积分作用和电机低速时定子电阻Rs变化引起的误差,保证辨识的磁链在全速度范围内精确。Ucomp由PI调节器调节电压模型和电流模型得到的定子磁链的差值得到:

通过调节Kp、Ki使得系统在低频时电流模型起作用,高频时电压模型起作用,从而使得两个模型平滑过渡。
利用改进的电压模型结合方程(3)、(4)得到在静止坐标系下的转子磁链为:

在新的磁链辨识系统中,可以在大范围内同时准确估计定子磁链和转子磁链,将得到的定子磁链用于 DTC,转子磁链用于MRAS中估计转速,可以在全速度范围内准确应用于使得整个系统。
在 MRAS中,利用新的磁链辨识方程作为参考模型,根据方程(2),在静止坐标系下,即 ωe=0时得到的带有转速 ωr的电流模型的磁链辨识方程为可调模型:

由方程(13)、(14)、(15)、(16)构成了新的 MRAS系统估计转速,如图2所示。
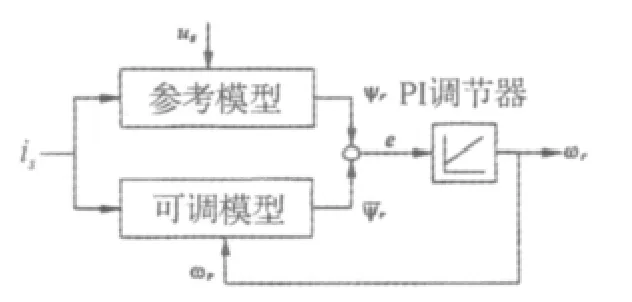
图2 MRAS结构图
2 模糊速度调节器
本文用模糊逻辑速度调节器代替传统的PI调节器,经典的模糊控制器需要三个步骤:输入变量的模糊化,模糊推理,解模糊,如图3所示。输入为速度反馈值与给定值的误差e和误差的微分ce,输出为du,输入输出的值都进行了归一化处理,Ke、Kce、Kdu为量化因子,为了提高动、静态的性能,本文选择三角形作为隶属函数,各个信号的模糊集及其定义模糊集合如下:
Z=零 PS=正小 PM=正中 PB=正大 NS=负小NM=负中 NB=负大 PVS=正很小 NVS=负很小
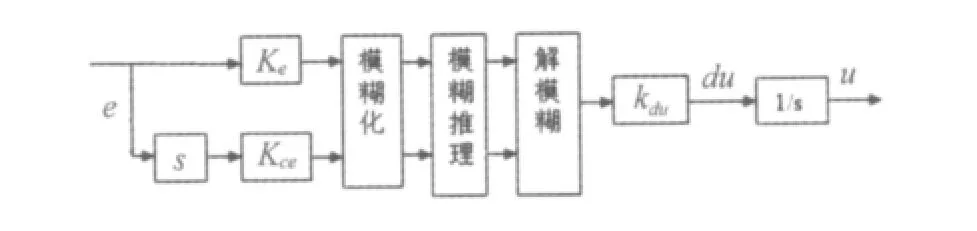
图3 模糊速度调节器结构图
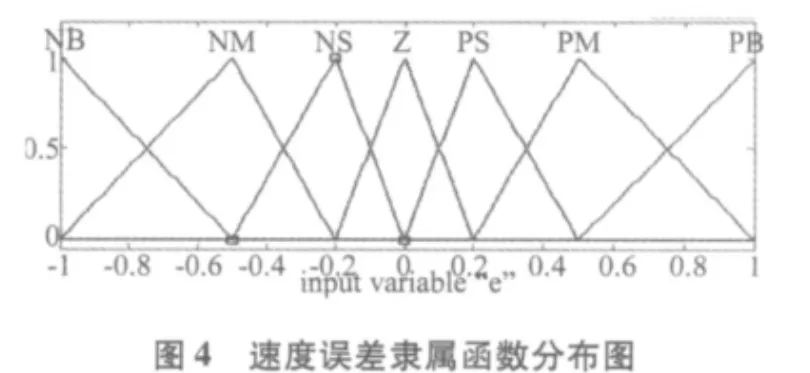
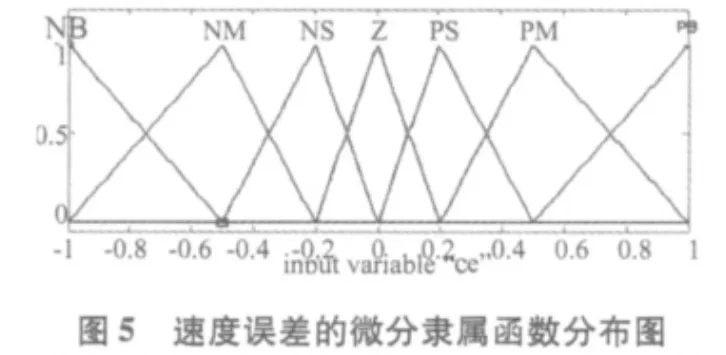
涵盖整个区间各变量的论域用单位值表示,信号e(pu)和ce(pu)有7个隶属函数,而输出有9个隶属函数,因为在原点附近要求的信号更加精确,用重心法进行解模糊。表1给出了对应的规则表,对应的隶属函数分布如图4~7所示。

表1 模糊速度调节的规则矩阵
3 仿真结果

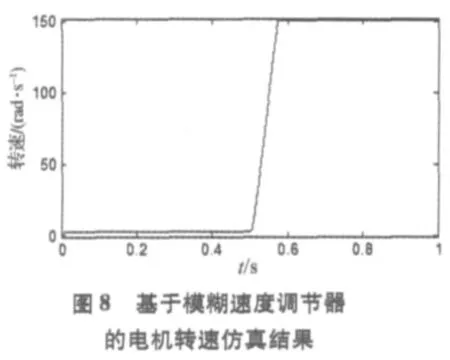
用MATLAB/SIMULINK进行仿真,仿真实验中用到的参数为:定子磁链幅值给定值为1 Wb,调节限定误差为0.01 Wb,转矩调节限定误差为0.5 N*m,直流侧电压为600 V,控制周期为2e-5 s。电机为空载时,0s时给定转速值为1 Hz,在0.5 s时给定转速值突变为50 Hz,仿真结果如图8,9所示。从图中可以看出新的磁链辨识方法可以在电机极低的转速下稳定应用,并且当定子电阻发生变化时,仍然能够准确的辨识电机转速。
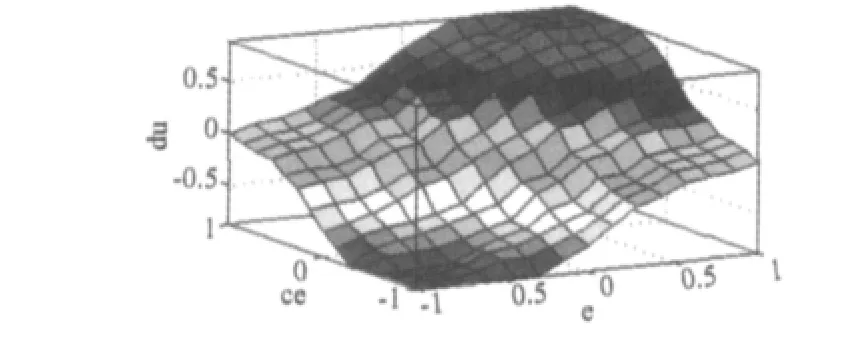
图7 模糊速度调节器的控制曲面图
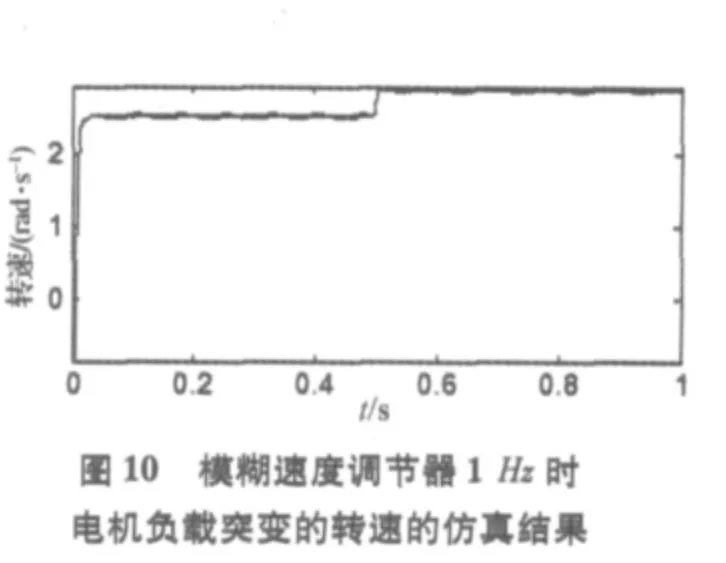
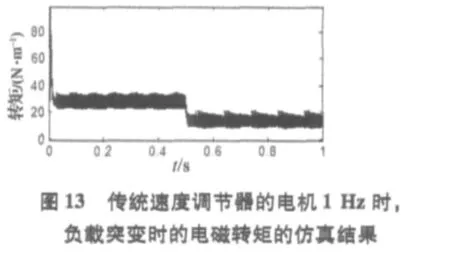
当电机给定为1 Hz(3.14 rad/s),给定初始负载转矩TL=28 N*m,0.5 s突变为14 N*m 时(电机额定转矩为 14 N*m),仿真结果如图10~13所示。从图中看出,电机给定为极低转速时,本文中基于模糊速度调节器的方法在2倍额定负载转矩下启动,相比传统的PI速度调节器,稳定精度提高了一倍。
4 结束语



本文提出了一种了新的磁链辨识方法,以克服传统U-I模型的积分饱和作用和低速定子电阻测不准带来的影响,由此方法构成的新的MRAS速度辨识系统可以在很大速度范围内准确辨识电机转速;文中用模糊速度调节器代替了传统的PI速度调节器,获得了更好的系统性能。
[1]李永东.交流电机数字控制系统[M].北京:机械工业出版社,2002:260-299.
[2]Bimal K.Bose,王聪,等译.Modern Power Electronics and AC Drives[M].北京:机械工业出版社,2005.450 -470.
[3]陈伯时,杨耕.无速度传感器高性能交流调速控制的三条思路及其发展建议[J].电气传动,2006,36(1):3 -8.
[4]徐安德.直接转矩最优控制研究现状及展望[J].信息技术,2007,11(1):145-147.
[5]Lascu C,Boldea I,Blaabjerg F.A Modified Direct Torque Control for Induction Motor Sensorless Drive[J].IEEE Trans,2000,1(36):122-130.
[6]Zhang Yongchang,Zhu Jianguo,Zhao Zhengming.An Improved Direct Torque Control for Three-Level Inverter-Fed Induction Motor Sensorless Drive[J].IEEE Trans,2010,5(21):1 - 12.
[7]王成元.电机现代控制技术[M].北京:机械工业出版社,2006:182-198.
