带钢热连轧工作辊温度场与热凸度的数值模拟

李维刚 ，刘相华，郭朝晖

(1.东北大学 信息科学与工程学院，沈阳 110819；2.东北大学 研究院，沈阳 110819；3.宝钢集团有限公司 中央研究院，上海 201900)

热轧带钢工作辊的温度场和热变形的影响因素多，边界条件复杂，是板形研究中的热点问题[1]。弯辊作为常规板形控制手段，对复合波、局部波等较复杂的板形缺陷修正能力有限，而利用热辊形可对工作辊有载辊缝的局部形状进行控制，配合弯辊得到优良板形[2]。因此，研究工作辊的温度场与热变形行为对板形控制有重要意义[2]，对轧辊的使用与管理具有重要参考价值。

对轧辊温度和温度场已有大量研究，可归纳为解析法、有限元法和差分法3种。解析法由于包含假设条件较多，一般仅用于温降过程的简单计算，UNGER曾采用解析法计算轧辊温度[3]。有限元法[4-9]计算结果精确，能够考虑复杂边界条件和材料特性等因素，但有限元法的问题在于数学概念复杂，一般常用于离线计算。差分法数学概念直观，便于考虑复杂边界条件，能快速准确计算稳态或非稳态温度变化。盐崎宏行[3]、GINZBURG[10]、杜凤山等[1]、郭振宇等[11]、王连生等[12]和杨利坡等[13]都曾分别建立了工作辊温度场的差分模型，从工程实用考虑，差分法已成为当前较实用的轧辊温度场在线算法。除冯明杰等[4]提出将轧辊内温度分为高频和低频非稳态温度波来研究以外，以往研究者对轧辊温度场的频域分析涉及很少，轧辊内不同深度处温度场频率的特性存在较大差异，这方面的研究有待进一步深入。此外，对高速旋转的轧辊受热与冷却边界条件的加以精细处理并做出评价一直是困扰人们的难题，到目前为止未能得到圆满解决。

本文作者考虑轧辊温度场在轴向和径向变化的特点，建立径向隐式、轴向显式的温度场差分模型，考虑工作辊圆周方向的周期性动边界条件，从而使建立的差分模型更贴近实际生产，满足实时跟踪计算的速度和精度要求。采用边界分区逐一处理与等效处理两种方式求解轧辊温度场，进而把轧辊温度场分解为低频分量和高频分量，研究两者在一个轧制周期中的变化规律。

1 轧辊温度场与热凸度模型

1.1 轧辊传热的基本方程

轧辊温度场为三维非稳态场，在轧制过程中，轧辊轴向、径向和周向的温度都要发生变化。假设轧辊轴向对称，轧辊温度计算归结为对称二维圆柱体第二类边值问题：

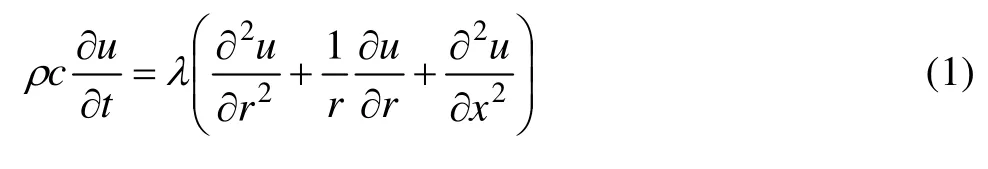
式中：ρ、c、λ分别为轧辊材料的密度、比热容和导热系数；r、x分别为轧辊径向、轴向坐标；u为工作辊的温度；t为时间；；q(x,t)、f (r,t)分别为轧辊轴向辊面边界条件函数、径向辊面边界条件函数；为各点温度初值。

1.2 轧辊温度场的差分模型

选取1/4工作辊作为分析对象，建立轧辊温度场轴向对称差分模型如图1所示。图中Nr为径向单元数，Nx为轴向单元数；i和j分别为径向和轴向的单元编号；①为轧辊辊颈与轴承热交换区，②为轧辊与空气热交换区，③为轧辊与冷却水热交换区，④为轧辊与带钢热交换区。

图1 轧辊温度场轴向对称差分模型Fig.1 Axially symmetric difference model of work roll temperature field

考虑到显式差分是有条件稳定的，而隐式差分计算量大，为了满足轧辊温度实时跟踪计算的要求，本研究力求在稳定性和计算量之间达成平衡，采用径向隐式、轴向显式的差分格式，确保在径向无条件稳定，同时总体计算速度较快。根据式(1)列写径向隐式、轴向显式的差分方程：

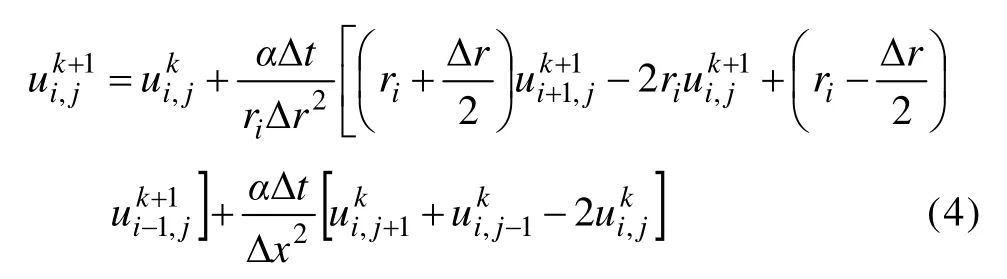
式中：k为时间步编号；Δt为时间步长；Δx为轴向长度；Δr为径向单元长度；ri为轧辊径向第i点的坐标；α为热扩散率，α=λ/(ρc)。式(4)经整理得到：

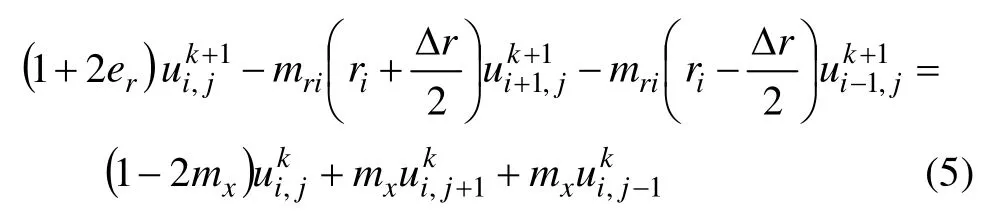
对边界面及边界角点根据热量平衡关系建立差分式，结合轧辊内部节点的差分式(5)，得到方程组：

因为方程组(6)中矩阵为三角阵，可用追赶法实现快速求解。

1.3 轧辊热凸度模型

由于轧辊内部存在不均匀温度场，使得辊身轴向产生不均匀热膨胀，进而形成轧辊热凸度。在温度分布已知的情况下，轧辊热变形可作为弹性力学问题求解，轧制过程中辊身表面j点k时刻的热膨胀量为

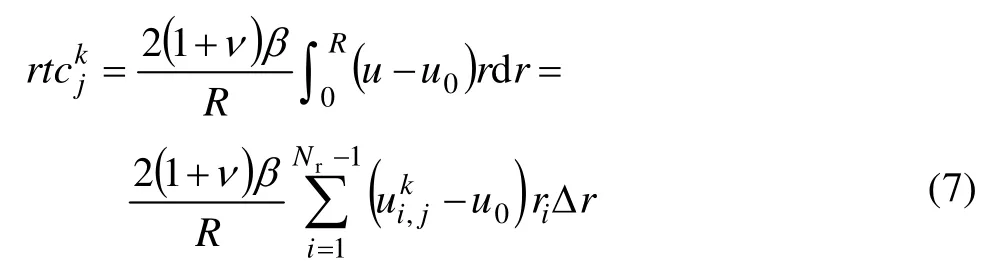
2 换热边界条件

轧辊温度计算的关键问题在于边界条件处理[3]，包括轧辊转动中各传热、冷却区域的划分，边界条件及相关参数的选择和确定，边界条件的处理模式及等效方式的确定等。

2.1 换热过程

轧辊轴向对称模型的换热过程如图1所示：AB为绝热过程；BC为轧辊与带钢的接触传热(轧制阶段)或空气自然冷却(间歇阶段)；CD为轧辊与冷却水的热交换；DE与EF为空气自然冷却；FG为辊颈与轴承的热交换；GH为空气自然冷却；HA为绝热过程。

另外，工作辊旋转一周过程中轧辊表面(BD边)将经历不同的热交换过程，本研究将圆周方向的热交换过程分为10个区域，6种情况，如图2所示。图2(a)所示为工作辊冷却水喷嘴和挡水板的周向布置方式，图2(b)所示为工作辊圆周方向的热换条件分区。

图2 工作辊圆周方向换热边界条件Fig.2 Heat transfer boundary condition of circumferential direction for work roll: (a)Work roll cooling diagram;(b)Boundary condition zones of heat transfer of roll circumferential direction

6种换热情况如下：1)Z1，轧制时轧辊与带钢接触传热，工作辊温度升高的热量来源，表面温度迅速上升，间歇时为空气自然冷却；2)Z2和Z10 ，主要为带钢对工作辊的辐射；3)Z3 和Z9 ，挡水板积水换热，由于冷却水在挡水板间的积水，使工作辊表面温度降低；4)Z4和Z8，直接水冷换热，是工作辊冷却的主要途径，通过安装在出入口的冷却水集管对轧辊表面进行强制冷却；5)Z5和Z7，空气自然冷却；6)Z6，与支撑辊的接触传热。

2.1.1 接触传热

1)与带钢接触传热(Z1)

工作辊与带钢接触传热是一个十分复杂的过程。一方面，在接触区内存在氧化铁皮、冷却水、润滑油等其它介质；另一方面，两固体的实际接触表面不可能是理想的光滑表面，即所谓“粗糙接触”。本研究采用换热边界条件：

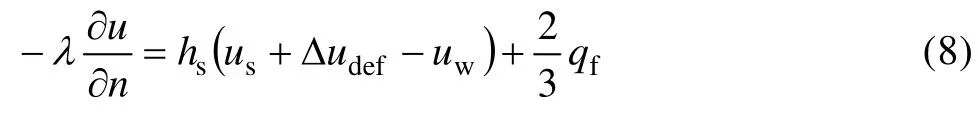
式中：n为工作辊表面的外法线方向；hs为带钢与工作辊之间的换热系数；us为带钢的表面温度；uw为工作辊的表面温度；Δudef为带钢变形温升；qf为摩擦热流密度。

对于热连轧带钢，换热系数hs可表示为[14]：

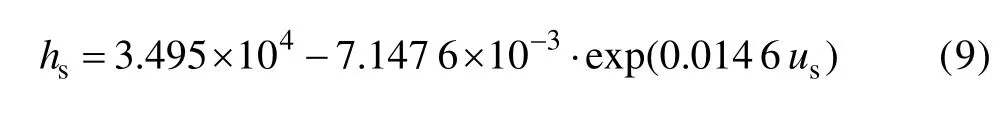
由于带钢变形而引起的温升：

式中：ρs为带钢的密度；cs为带钢的比热容；σdef为带钢的屈服压力；β为压缩比。2)与支撑辊接触传热(Z6)

工作辊与支撑辊的传热过程也是接触传热，采用SABOONCHI和 ABBASPOUR[14]提出的公式计算其边界条件：

式中：hb为支撑辊与工作辊之间的换热系数；ub为支撑辊的温度。

换热系数的表达式如下：

式中：Δθ为支撑辊与工作辊之间的接触角；Lc为摩擦弧长；Vr为工作辊的线速度。

2.1.2 强制水冷

1)档水板水冷(Z3和Z9)

为保证对工作辊的充分冷却，同时避免大量工作辊冷却水喷射到轧件表面，在轧件上方沿工作辊轴向装有挡水板，使工作辊冷却水从工作辊两侧流失，这样在挡水板上会存在一定量的积水，这部分积水对工作辊也会有冷却作用。根据文献[15]，挡水板处的积水与工作辊表面间的换热系数hww为

式中：Re为雷诺数；Prcw为挡水板积水的Prandtl常数；lww为挡水板积水与工作辊接触弧长；λw为水的导热系数；cw为冷却水的比热容；νcw为冷却水流动粘度；ρw为冷却水的密度。

2)直接水冷(Z4和Z8)

工作辊热量主要通过喷水冷却带走，冷却水与工作辊表面之间的换热是一种强制对流换热，对流换热系数hcw值与冷却水压力、温度、喷嘴与工作辊表面的距离、喷射角度及喷射水量密度等因素有关。在考虑这些因素的基础上，对流换热系数可由下式[15]计算：

1)当工作辊表面温度uw＜100 ℃时

2)当工作辊表面温度uw＞200 ℃时

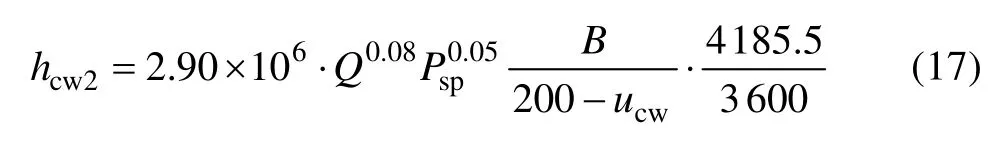
3)当工作辊表面温度100 ℃≤uw≤200 ℃时

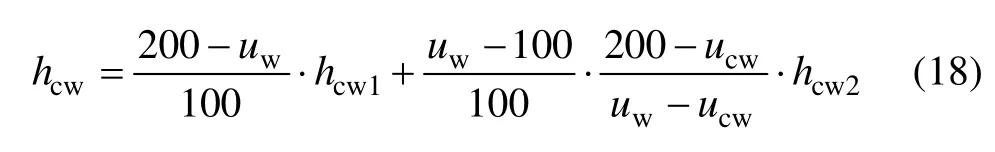
式中：Q为水流密度，Q= Vsp/Asp；Vsp为冷却水量；Asp为喷射面积；Psp为喷射压力；ucw为冷却水温度；当Q＜10 000 L/(s·m-2)，B=(ucw/16)-0.17；当Q≥10 000 L/(s·m-2)，B=1。

2.1.3 辐射换热(Z2和Z10)

在工作辊咬入钢坯前，Z10区与轧前带坯表面、前挡水板构成辐射换热系统；在钢坯抛出后，Z2区与轧后带坯表面、后挡水板构成辐射换热系统。这两个区域的换热根据文献[14]采用的方法求出。

2.1.4 空气自然冷却(Z5、Z7和间歇时Z1)

采用对流和大空间辐射换热综合边界条件，即

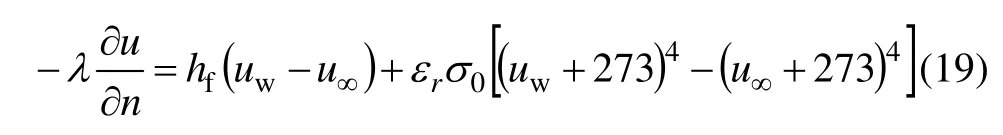
式中：hf为工作辊表面与周围空气之间的对流换热系数；u∞为工作辊周围空气的温度；εr为工作辊的表面温度；σ0为Stenfan Boltzmann常数。

2.2 等效方式

通过数值模拟对各种边界处理方式作比较，寻找能满足实时计算要求的速度、精度和稳定性都适宜的等效处理方式。工作辊圆周方向的热交换过程通常存在两种等效方式。

1)边界等效处理，按弧长比例对圆周方向各区域边界条件做加权处理，即

式中：qequ为总等效热流密度；li代表各区域的圆周弧度；qi代表各区域的热流密度，由换热边界条件计算得到。

2)边界逐一处理，对图2中的10个分区的边界条件进行逐一处理，根据轧辊旋转一周依次经历的不同换热分区，依次施加相应的换热边界条件qi，藉此将轧辊圆周方向坐标转化为时间坐标。

对某同宽轧制计划的工作辊温度场进行数值模拟，主要参数：轧辊材质为高速钢辊，轧辊直径 830 mm，线速度1.24 m/s；轧件宽度1 140 mm，轧件温度1 022 ℃；轧制时间70 s，间隙时间40 s, 轧制周期共60卷带钢。图3所示为采用转1周逐一处理、转动1周等效处理和转动5周等效处理的温度计算结果(轧辊中心横截面x=0处，仅画出前6卷)。

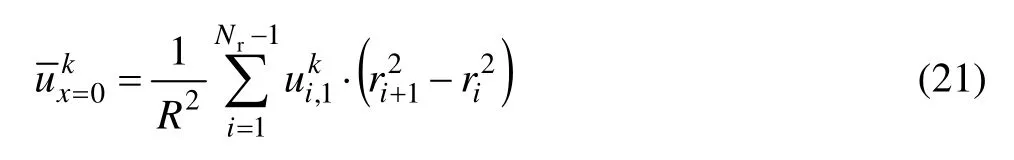
由图3可见：①转动1周逐一处理与等效处理的轧辊表层温度有一定差异，但径向平均温度几乎相等，可将轧辊转动的复杂边界条件用等效边界条件替代；②在一定误差范围内，可将轧辊转动几周(对F7机架甚至是几十周)的温度计算处理成1次计算，这将大大减小模型计算次数，使轧辊温度的在线实时跟踪计算得以实现。

3 实验验证

为了验证模型的可靠性和计算精度，用C++语言编制了轧辊温度场及热凸度离线模拟计算程序。现以宝钢1880热连轧某一轧制计划为例，对F7机架工作辊的温度场及热凸度进行离线模拟分析。该轧制计划共53卷带钢，轧件温度908 ℃、轧辊速度9.3 m/s，轧制时间70 s，间歇时间43 s。计划结束后，立即停掉机架水，将轧辊从机架中抽出，用接触式温度计测量轧辊表面温度，考虑到对称性，只测量辊身长度的一半，每隔100 mm测1点。图4所示为计算值与实测值的比较。由图4可见，误差在3 ℃以内，说明模型可以较准确计算轧辊的温度场分布。

利用GS-332 辊形测量仪对下线后的热态辊形和冷态辊形进行测量。两者差值为工作辊的热膨胀量，图5所示为测量值与模型计算值的比较。由图5可见，误差在10 μm以内，测量值与计算值吻合较好。

4 分析与讨论

4.1 轧辊温度场

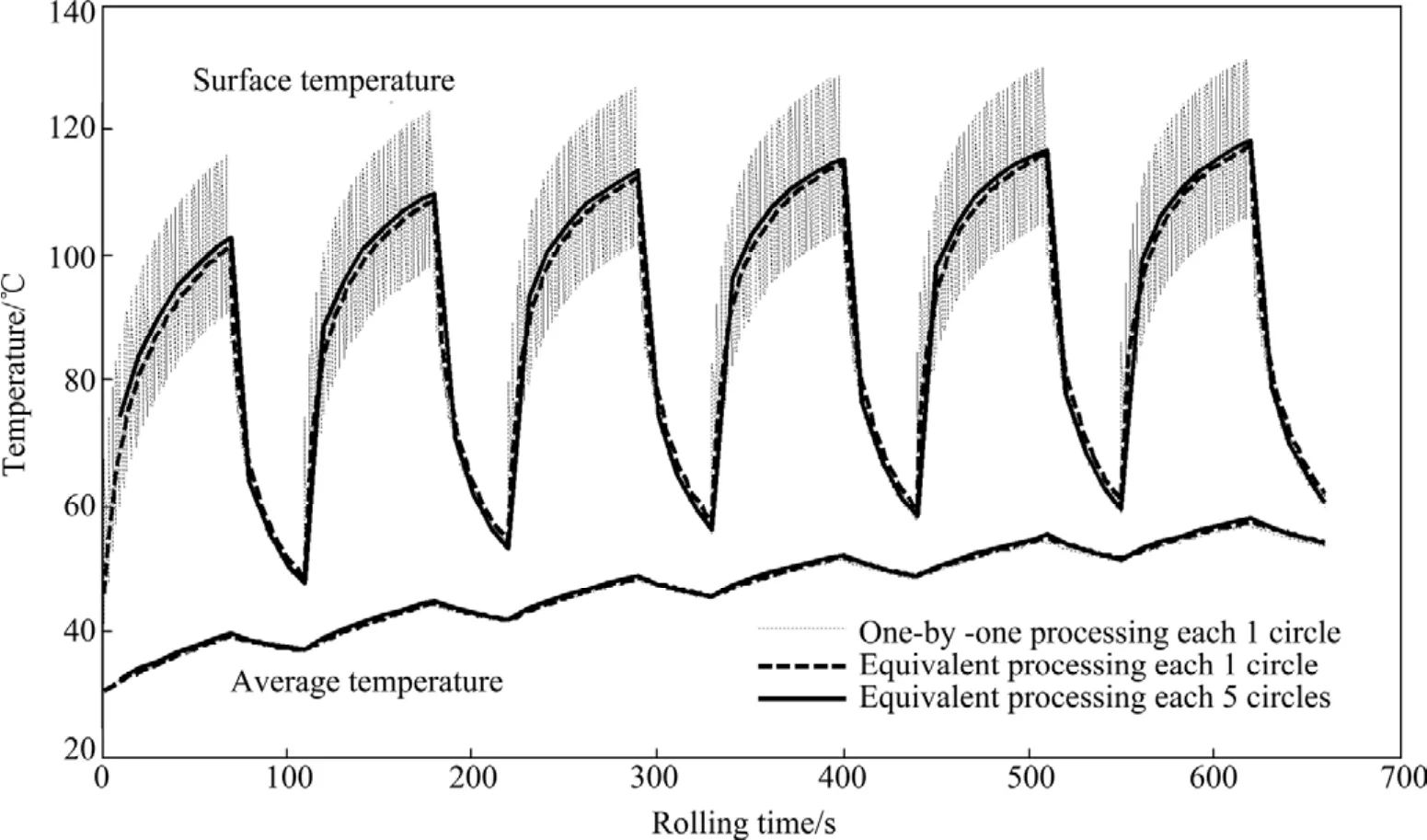
图3 边界逐一处理与等效处理时的结果对比Fig.3 Result comparison between one-by-one and equivalent boundary conditions

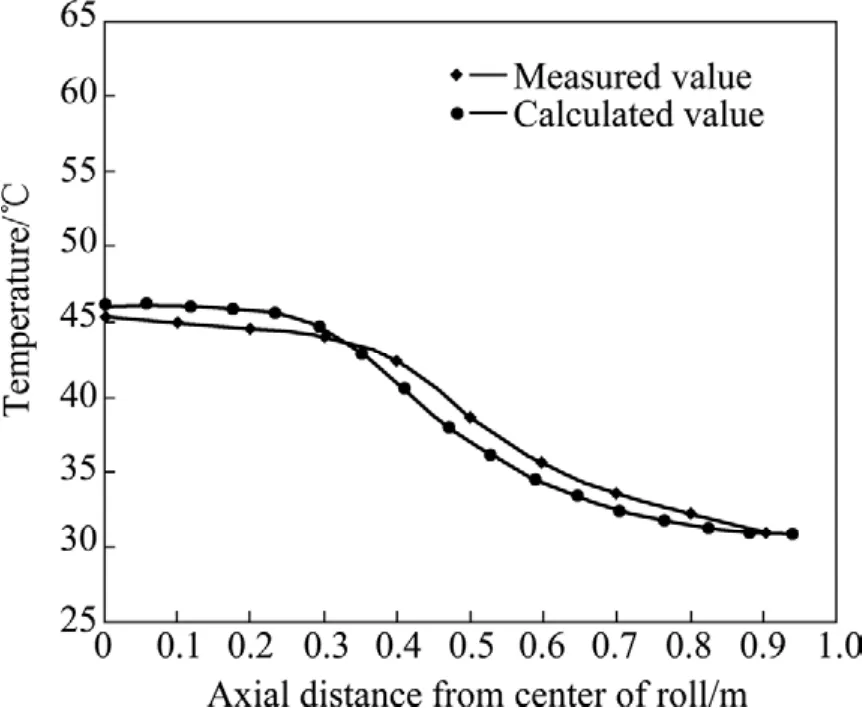
图4 轧辊表面温度实测值与计算值Fig.4 Measured and calculated roll surface temperatures

轧线生产连续进行时要周而复始地经历轧制阶段和间歇阶段，两个阶段工作辊的换热条件不同，轧辊在转动1周过程中辊面所经历的换热过程也不相同。因此，从边界条件的交变特性考虑，轧辊内温度变化可分解为两部分：1)以轧制1卷带钢经历的时间为周期的低频分量；2)以轧辊转动1周经历的时间为周期的高频分量，轧辊传热是这2种分量共同作用的结果。

分析可知，边界等效处理求得的结果实际上为圆周方向总的温度均值(周向平均温度)，属于轧辊温度的低频分量；而边界逐一处理求得的结果为轧辊圆周方向各区域的温度均值。从后者减去前者，可分离出轧辊温度的高频分量。

对2.2中相同的轧制计划，下面分别通过边界等效处理和边界逐一处理求解轧辊内温度场。

图5 轧辊热膨胀量实测值与计算值Fig.5 Measured and calculated roll thermal expansions

图6所示为边界等效处理求得的轧辊中心横截面(x=0)处距轧辊表面不同深度的温度曲线，即低频分量。由图6可见：①轧辊内不同深度的温度处于周期性的变化中，内部温度随表面温度的波动而波动，但随着深度的增加，温度波动的幅度衰减较快，这是因为温度在向轧辊内部传递过程需要时间且存在向附近扩散；②轧制初期，无论是表面温度还是内部温度，都呈上升趋势，在轧制一定数量的带钢后，不同深度处的温度会渐渐趋于一个动态稳定值；③距离表面越远的位置，达到稳态所需时间越长，温度曲线a为轧制约8卷带钢后基本达到动态稳定状态，温度曲线b、c和d则分别在第12 、22、40卷后不再有明显的上升趋势；④轧辊中心的温度曲线e和径向平均温度曲线f在整个过程中都保持上升趋势，轧制60卷后仍未能达到稳定值。

图6 轧制过程中轧辊不同深度处温度的低频分量Fig.6 Low frequency component of roll temperature in different penetrations during rolling process

再通过边界逐一处理求解轧辊内温度场，结果如图7所示(为清晰，仅给出前3卷)。用边界逐一处理结果与边界等效处理结果做差，分离出高频分量，如图8所示。比较图6和8可知：低频分量是轧辊温度的主要成分，高频分量随着深度的增加衰减很快，其影响深度有限，仅在距轧辊表层10 mm以内的范围有明显影响，对轧辊径向平均温度及轧辊热变形影响很小，这为计算与板形控制相关的热凸度时采用边界等效处理方法提供了依据。

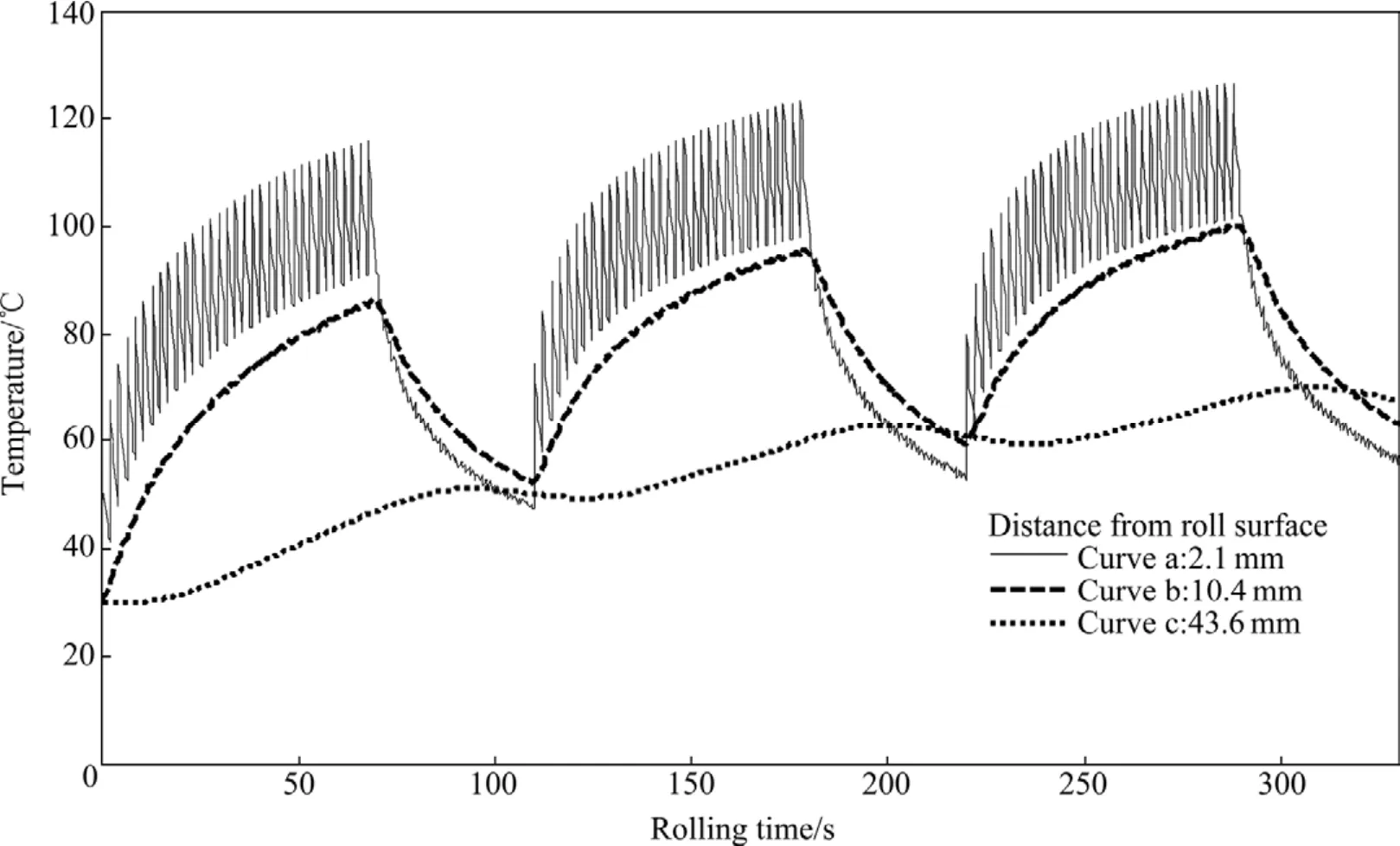
图7 轧制过程中轧辊不同深度处的温度分布Fig.7 Temperature distribution of work roll in different penetrations during rolling process

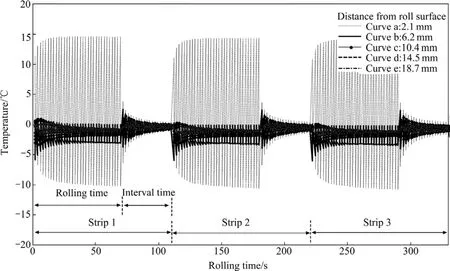
图8 轧制过程中轧辊不同深度处温度的高频分量Fig.8 High frequency component of roll temperature in different penetrations during rolling process

根据图6和8，可求得轧制过程中轧辊温度低频分量与高频分量波动的幅度，图9所示为一卷带钢温度的波动幅度(各卷波动幅度基本相同)。由图9可见，低频分量波动幅度在辊面以下超过40 mm时还有7.2℃，而高频分量波动幅度在辊面以下 10 mm时仅有4.5 ℃，本研究把这种现象称为轧辊温度高频分量的“浅层效应”。“浅层效应”的分析对于轧辊外层材质的选取、轧辊表面失效分析及轧辊冷却水的工艺优化等方面具有重要参考价值。

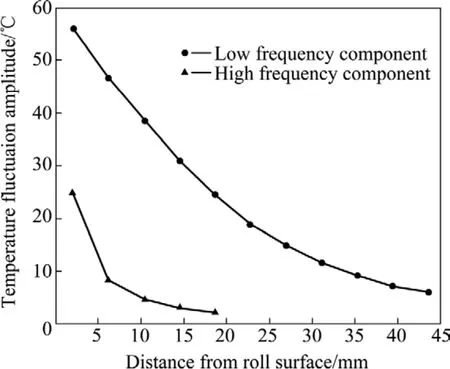
图9 一卷带钢轧制过程中轧辊不同深度处温度的波动幅度Fig.9 Fluctuation amplitude of roll temperature in different penetrations during rolling process of one strip

需要注意的是，在实际生产过程中，轧辊旋转一周，局部区域的瞬间温度可高达几百摄氏度，但持续时间很短。由于本研究采用有限差分法，在圆周方向的计算单元有限，因而计算出的轧辊温度高频分量的变化幅度比实际情况要小一些，但其基本趋势和实际生产是一致的。

4.2 轧辊热凸度

将4.1节中的轧制计划延长至120卷带钢，模拟计算轧辊全长热凸度CT(指轧辊辊身在中部和边部对应的轧辊直径差)及有效轧辊热凸度CP(指带材中部和带材边部对应的轧辊直径差)的变化过程，结果如图10所示。

由图10可见：①轧辊热凸度连续周期性变化，形成动态热变形。这是由于高温轧件与轧辊间的接触传热和冷却水的喷射冷却、空气的对流冷却，同时轧辊温度受压下量、轧制速度、板宽、带钢长度、轧件温度、轧制节奏、冷却条件等一系列工艺因素的影响，轧辊温度处于不稳定状态；②轧制初期热凸度增加明显，呈指数上升趋势，轧制后期热凸度趋于一个动态稳定值，轧辊有效热凸度CP和轧辊全长热凸度CT分别在轧制50 卷、70 卷带钢后达到稳态。这是由于轧制初期轧辊温度低时温度上升快，热凸度增加也较快；轧制一定数量的带钢后，吸收的热量与散失的热量接近平衡，轧辊热凸度处于一个动态稳定值。

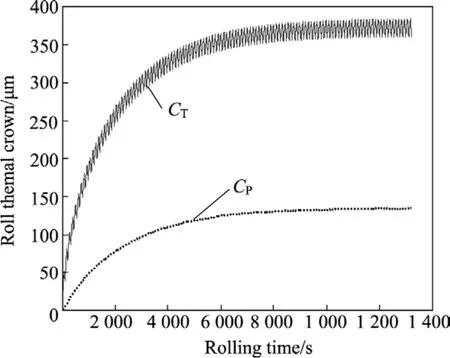
图10 轧制过程中轧辊热凸度随时间的变化Fig.10 Change of roll thermal crown with rolling time during rolling process

通过上述分析可知，可采用上述方法建立现场在线动态热凸度模型，将一个轧制计划热凸度控制过程分为两部分：1)轧制初期，通过本研究计算结果拟合为指数型热凸度参数变化曲线；2)轧制带钢达到一定批量后，可将热凸度设定为恒定值。

5 结论

1)考虑热轧带钢工作辊的边界条件，建立了工作辊温度场的径向隐式、轴向显式的差分模型，通过数值模拟与现场实测轧辊表面温度和热膨胀量的对比表明，轧辊表面温度计算值与实测值偏差在3 ℃以内，轧辊热膨胀量计算值与实测值偏差在10 μm以内，吻合较好。

2)在轧辊温度场的数值模拟计算中，提出两种边界条件的处理方法：一是把轧辊表面分为10个区间、6种情况的分区逐一处理方法，二是按照各区弧长加权的等效处理方法。对两种处理方法做了比较，发现两者对接近轧辊表面处，温度计算结果差别较大；而对轧辊径向平均温度和热凸度的计算结果差别不大，等效处理方式可用于板形控制中的轧辊热凸度计算。

3)采用上述两种处理方法进行模拟计算发现，轧辊温度可分解为以轧制1卷带钢所经历时间为周期的低频分量和以轧辊转动1周所经历时间为周期的高频分量，其中低频分量是轧辊温度场的主导因素，而高频分量仅在轧辊表面 10 mm以内有明显影响，存在“浅层效应”，它对轧辊外层材质的选取、轧辊表面失效分析及轧辊冷却水的工艺优化等方面具有重要参考价值。

4)轧制初期轧辊内温度变化较快，热凸度呈指数上升趋势，轧制一定数量的带钢后，吸收的热量与散失的热量接近平衡，热凸度处于动态稳定状态，据此可建立两段式轧辊热凸度在线计算模型，在一个轧制计划初期采用指数型模型计算轧辊热凸度，后期热凸度可采用恒定值。

[1]杜凤山, 于 辉, 郭振宇.板带热轧工作辊温度场的研究[J].塑性工程学报, 2005, 12(2): 78-81.DU Feng-shan, YU Hui, GUO Zhen-yu.Study on temperature field of hot strip work roller[J].Journal of Plasticity Engineering,2005, 12(2): 78-81.

[2]YANG L P, PENG Y, LIU H M.Two-dimensional transient temperature field of finish rolling section in hot tandem rolling[J].Journal of Iron and Steel Research International, 2004,11(4): 29-33.

[3]王国栋.板形控制和板形理论[M].北京: 冶金工业出版社.1986: 389-438.WANG Guo-dong.Shape control theory[M].Beijing:Metallurgical Industry Press, 1986: 389-438.

[4]冯明杰, 王恩刚, 赫冀成.带钢热连轧机工作辊非稳态传热的数值模拟[J].金属学报, 2010, 46(8): 1009-1017.FENG Ming-jie, WANG En-gang, HE Ji-cheng.Numerical simulation on unsteady state heat transfer of work rolls during continuous hot strip rolling[J].Acta Metallurgica Sinica, 2010,46(8): 1009-1017.

[5]GUO Z F, LI C S, XU J Z, LIU X H, WANG G D.Analysis of temperature field and thermal crown of roll during hot rolling by simplified FEM[J].Journal of Iron and Steel Research International, 2006, 13(6): 27-30.

[6]ABBASPOUR M, SABOONCHI A.Work roll thermal expansion control in hot strip mill[J].Applied Mathematical Modeling, 2008, 32: 2652-2669.

[7]PARK C M, CHOI J T, MOON H K, PARK G J.Thermal crown analysis of the roll in the strip casting process[J].Journal of Materials Processing Technology, 2009, 209: 3714-3723.

[8]YUAN S Y, ZHANG L W, LIAO S L, JIANG G D, YU Y S, QI M.Simulation of deformation and temperature in multi-pass continuous rolling by three-dimensional FEM[J].Journal of Materials Processing Technology, 2009, 209: 2760-2766.

[9]高建红, 黄传清, 王 敏, 黄建平.基于 ANSYS的热轧工作辊温度场的有限元分析[J].塑性工程学报, 2009, 16(3):218-221.GAO Jian-hong, HUANG Chuan-qing, WANG Mei, HUANG Jian-ping.Finite element analysis of temperature fields of work roll in hot rolling mill based on ANSYS[J].Journal of Plasticity Engineering, 2009, 16(3): 218-221.

[10]GINZBURG V B.Application of coolflex model of analysis of work roll thermal conditions in hot strip mills[J].Iron and Steel Engineer, 1997(11): 38-45.

[11]郭振宇, 安 强, 程 博, 曹秉刚.差分演化算法在热连轧工作辊温度场仿真中的应用[J].系统仿真学报, 2007, 19(21):4877-4880.GUO Zhen-yu, AN Qiang, CHENG Bo, CAO Bing-gang.Research on work roll temperature with improved differential evolution in hot strip rolling process[J].Journal of System Simulation, 2007, 19(21): 4877-4880.

[12]WANG Lian-sheng, YANG Quan, HE An-rui, ZHENG Xuan,YU Hong-rui.Improvement of prediction model for work roll thermal contour in hot strip mill[J].Journal of Central South University of Technology, 2010, 17(6): 1251-1257.

[13]杨利坡, 王东城, 于丙强, 王英睿.热轧辊瞬态温度场快速仿真模型[J].塑性工程学报, 2010, 17(1): 123-128.YANG Li-po, WANG Dong-cheng, YU Bing-qiang, WANG Ying-rui.Research on the quick simulation model for the transient temperature field of the hot roll[J].Journal of Plasticity Engineering, 2010, 17(1): 123-128.

[14]SABOONCHI A, ABBASPOUR M.Changing the geometry of water spray on milling work roll and its effect on work roll temperature[J].Journal of Materials Processing Technology,2004(148): 35-49.

[15]昌先文.轧辊热凸度模拟系统的开发[D].沈阳: 东北大学,2005: 36-46.CHANG Xian-wen.Development of simulation system of the roll’s thermal crown[D].Shenyang: Northeastern University,2005: 36-46.