自适应过滤法在磁悬浮陀螺全站仪观测数据预测中的应用研究
2012-12-11周志易杨志强
周志易,杨志强
(1.长安大学地质工程与测绘学院,陕西西安710054;2.合肥工业大学土木与水利工程学院,安徽合肥230009)
一、引 言
对于磁悬浮陀螺全站仪在定向的过程中,仪器采集的转子电流数据都是受环境影响的动态时间序列数据,由于受制造工艺及外界环境条件的影响,这些数据经常会偏离实际的真值。因此,当环境条件变化时,仪器若能科学预报观测数据的发展趋势将对仪器自动监测起到关键作用。目前,虽然仪器的精度和自动化程度都很高,但采集的数据是在动态变化的环境中完成的,因此,要客观地反映数据的发展变化过程,应采用动态的方法,其模型也应是动态模型,使之与环境变化相适应,来不断完善、改进观测数据分析和预报方法,以完善仪器的自动监测过程,使定向测量的数据不会偏离真值,即使有偏离,也应使定向测量的观测数据在合理的范围内。否则,将失去建立预测模型的意义,只能作为对过去所产生的数据的拟合,而没有预测未来的价值。由于环境变化的复杂性,至今仍处于探索性研究阶段。传统的基于数理规律的回归分析方法是一种静态的数据处理方法,不适用于动态数据分析处理[1]。本文就是基于磁悬浮陀螺全站仪采集的转子电流数据随时间变化的动态特征,应用自适应过滤法(self-adaptive filtering)这种近代时间序列分析的新方法来处理此数据。经分析可知,其观测值是影响仪器计算的定向角的精度的,而自适应过滤法适合于处理动态数据,因此,对仪器采集到的转子电流观测值进行分析,并建立动态模型,进而对仪器采集的数据趋势作出预报,以达到自动监测的目的。
二、自适应过滤法的基本原理
1.自适应过滤法的概念
设x1,x2,…,xt是某一随机过程观测的M个观测值的随机时间序列,则时间序列预测模型可表示为
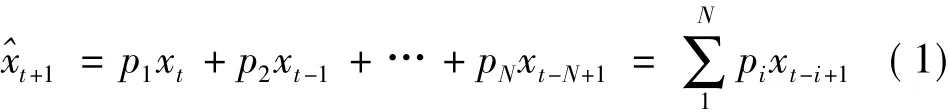
自适应过滤法就是从权系数的一组初始观测值开始利用式(1)作加权处理,并不断反馈迭代来调整权系数,以实现权系数的最优化。一般权系数的初始值可简单地取作pi=1/N。
2.自适应过滤法具体过程
用式(1)作预测的基本思想是认为过去的观测值不仅包含了未来发展的基本信息,而且包含了随机成分,通过加权平均处理可以保留发展的基本信息,离析随机干扰。其计算的基本过程是:
1)假定当前期t=N,取一组初始权数pi(i=1,2,…,N),按照式(1)计算下一期t+1时的预测值。
2)计算预测值和实际值之间的误差
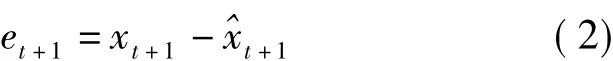
3)根据预测误差et+1调整权数以减少误差。如此反复进行,可找到一组“最佳”的权数,使误差减少到最低限度。其公式为
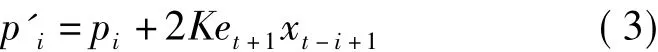
式中,p'i为调整后的第i个权数;K为学习常数。利用此方法对权数进行调整,从t=N开始到t=M称为一轮迭代。然后将得到的新的权数作为初始权数,重新开始下一轮迭代过程,如此反复进行至误差无多大改进时,即认为获得了一组最佳权数,并用来进行预测。初始权数取初始t=N,pi=1/N(i=1,2,…,N)。
3.学习常数K的选择
用式(3)调整权数源于数学上的最速下降法逼近,是依据数学中的最优化原理,以预测误差的平方最小为目标函数。这里K的取值是有一定限制条件的,否则自适应过滤法就不一定向最小误差收敛,经证明按照式(2)调整权数的自适应过滤法收敛的充分条件是[4]:,此式分母表示观测值时间序列中最大的N个观测值的平方之和。为了避免反复迭代四舍五入造成的收敛条件得不到满足,按照文献[1]可取学习常数
为了减少计算工作量和提高预测精度,还需要选取恰当的权数个数N。在观测值序列没有周期性选择时,N通常取2~6[5]。可以选择几个不同的N,最后选用产生预测误差最小的N值。对于含有周期性的数据,权数就是时间序列的周期。对于权数个数,也可通过现代时间序列分析模型的判定方法来判定下一期的发展同以往多少期关系较密切来判定[6-7]。
三、自适应过滤法应用于磁悬浮陀螺全站仪定向测量中的转子电流数据预报
在某隧道工程定向测量中,选用仪器在定向测量中采集的有代表性的转子电流的部分观测数据,利用自适应过滤法对此转子电流数据进行计算验证。笔者在选择权数的个数上遵循以上的选择原则,经时序分析模型的判定方法确定N=3,通过编程计算得到较好的结果,在选择数据上前几组数据来建立模型,用后面的10组数据进行预测检验。生成的模型为

为了进行比较,同时也建立了传统的统计回归模型[7-8]。由于观测数据有一定的起伏,因此统计模型选用样条回归分析模型,在数据选择上,同自适应过滤法一样用前几组数据来建立回归模型,对后面10组数据进行预测检验。
两种方法的计算结果如图1、表1所示。自适应过滤法有3个权数,从第4期开始迭代,所以前几期没有计算预测值,所建模型就是用来预测未来的数据的稳定性,以达到自动监测的目的。从图1与表1可以看出,从预测误差来看,自适应过滤法预测的误差较小,总体变化较为平稳。自适应过滤法10期预测值标准差为±1.689 1e-009,而传统的回归分析模型10期预测值标准差为±1.961 5e-011,自适应过滤法预测效果明显优于传统的回归分析模型。
自适应过滤法预测结果与实际观测值相近,误差很小。自适应过滤法用来预测仪器的转子电流数据是可行的,根据初期观测的稳定的数据建立的模型可以作为仪器在观测过程中的预测模型,以实现自动控制的目的。它不仅可用来作为未来转子电流稳定性的监测手段,也扩展了预测预报的方法,是一种较好的动态观测系统数据预处理的新方法。
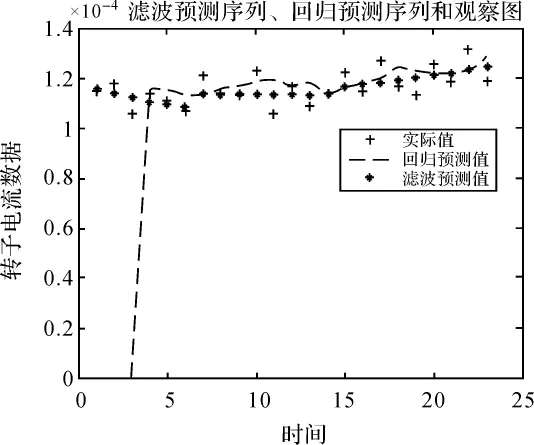
图1 两种模型预测值与实测值比较
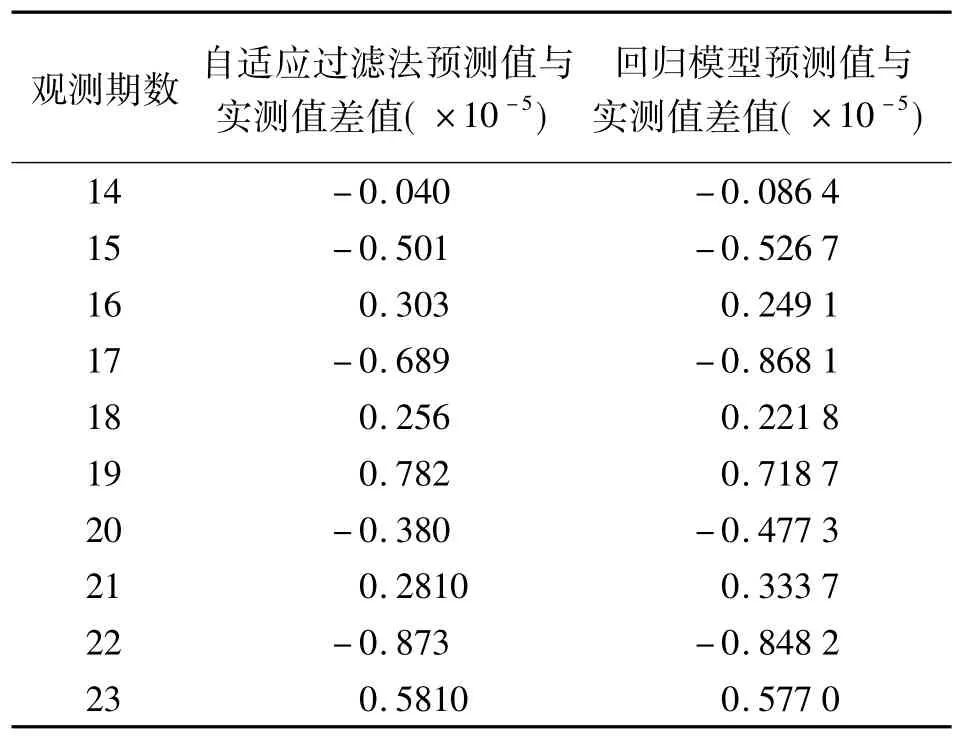
表1 预测值与实测值对比分析
四、结束语
本文针对传统的静态的数据处理方法不适应于对磁悬浮陀螺全站仪采集的转子电流的动态数据进行分析处理的问题,提出了利用自适应过滤法进行仪器采集的转子电流数据,以达到预测预报转子电流的稳定性。实际采集的数据通过编程计算,结果表明:
1)自适应过滤模型适用于高精度的磁悬浮陀螺全站仪的转子电流的分析预报,为使仪器在观测过程中采集的数据更稳定提供了理论模型。
2)此方法简单易行,可用标准程序上机运算,约束条件较少,具有自适应性。它能自动调整权系数,只要仪器初期采集的数据稳定可靠,运用此模型来监测数据的稳定性具有一定的发展空间和推广使用价值。
今后进一步将模型移植到仪器的功能模块中,以达到自动控制和监测数据稳定性的目的。
[1]尹晖.时空变形分析与预报的理论和方法[M].北京:测绘出版社,2002:1-5.
[2]赵敏,贾惠敏.自适应过滤法在火灾发展趋势预测中的应用[J].武警学院学报,2007,23(6):44-45.
[3]姚奇富,马华林,张国清.一个网络管理软件中基于自适应的流量预测[J].计算机测量与控制,2006,14(1):45-46.
[4]郝小员,郝小红.自适应过滤法在边坡变形破坏时间预报中的应用[J].华北水利水电学院学报,1998,19(1):53-55.
[5]周雄鹏.一种近代时间序列预测模型——自适应过滤法[J].外国经济与管理,1986(3):37-39.
[6]王振龙.应用时间序列分析[M].北京:中国统计出版社,2010.
[7]朱明英.ARMA模型的几种定阶方法[D].吉林:东北师范大学理学院,2007.
[8]黎昵,岳建平,段鹏.改进模糊神经网络模型及其在大坝监测中的应用[J].水电自动化与大坝监测,2007,31(1):74-76.
