基于多目标的TSP模型在物流配送中的应用

韦美雁

（湖南科技学院 计算机与通信工程系，湖南 永州 425100）

基于多目标的TSP模型在物流配送中的应用

韦美雁

（湖南科技学院 计算机与通信工程系，湖南 永州 425100）

本文以永州市为例，从配送中心的角度出发，以时间、费用、距离三个为参数指标，采用分支定界法建立多目标 TSP模型，然后使用基于粒子群算法的满意度模型对其进行评价，得到了最佳运输线路的设计方案，为配送中心设计运输线路提供理论依据和实用参考价值。

运输线路；TSP模型；PSO算法；物流配送

1 问题的提出

20世纪90年代末以来，随着国民经济的发展，我国物流业的发展势头迅速。物流配送中心作为物流供应链上的中心环节，上连供应商，下连终端客户，起着举足轻重的作用。而车辆作为物流配送中心重要的作业资源，其调度是否优化、行走路径是否合理，大大影响着物流中心的经营成本和服务质量。物流配送中心的车辆调度和运输路线安排的科学性[1]，直接影响企业的整体效益。因此，进行物流中心车辆调度和运输路线的优化研究是十分必要的。本文主要从物流配送中心的角度出发，考虑车辆调度和运输路线的优化设计中的距离、费用、时间等多个因素，建立了一个多目标TSP优化模型，并把该模型应用于湖南省永州市的物流配送中心车辆调度和运输路线的优化设计中，为永州市的物流配送中心车辆调度和运输路线的优化提供理论基础和参考依据。

2 多目标TSP模型

2.1 基本多目标TSP数学模型[2]

TSP是个典型的组合优化问题，属于NP完全问题（NP—Complete）之一。当问题的规模较大时，很难得到全局最优解或满意解，而且随着问题规模的增大，算法的计算时间将以指数速度增加。

多目标优化问题可以描述为求：

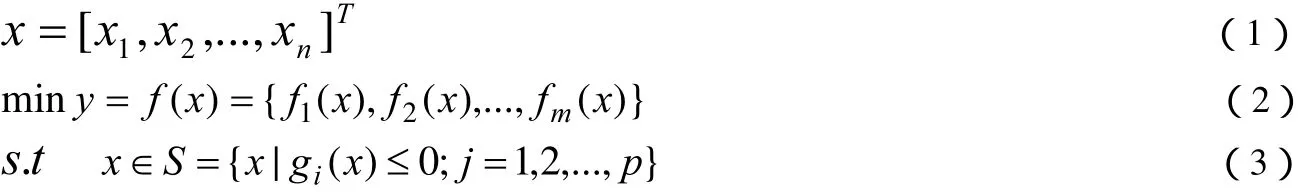
式中x为决策向量，y为目标向量，g(x)i为第j个约束，S为决策变量可行解域。本文中对旅游线路进行优化决策时，考虑三个指标：距离、时间和费用。其目标函数描述如下：

其中，xij=l表示从城市i到城市j的路径，xij=0表示没有这条路径，dij为第i个城市到第j个城市的距离，tij为从第i个城市到第j个城市消耗的时间，cij为第i个城市到第j个城市的费用。

2.2 基于PSO算法的满意度

在求解单目标优化时，人们寻找的是一个最好的解，这个解比其它所有的解都要好。当我们求解多目标优化问题时，由于有多个目标且存在目标之间的无法比较和冲突现象，要使所有的目标函数同时达到最大（或最小）是不可能的，一个解可能在其中某个上是最好的，但在其他目标上是最差的，不一定有在所有目标上都是最优的解，但是，可以存在这样的解：对一个或几个目标函数不可能进一步优化，对其他目标函数不至于劣化，这样的解称之为非劣最优解（Pareto optimal）。情况下，最优解不只一个，而是一个最优解集。多目标算法的工作就是，构造非支配集，并使非支配集不断逼近Pareto最优解集，最终达到最优。

定义1 对于最小化问题，若'x是搜索空间中一点，当且仅当不存在i（在搜索空间中）使得成立，说'x为非劣最优解。

定义2 所有非劣最优解组成的集合称为多目标优化问题的最优解集（Pareto optimal set），也称为可接受解集或有效解集。

定义3 通过对各目标进行单目标优化来获得各个目标的最优解，将其作为评价多目标优化解的指标，称这些解为理想解。

定义4 多目标优化解的满意度为

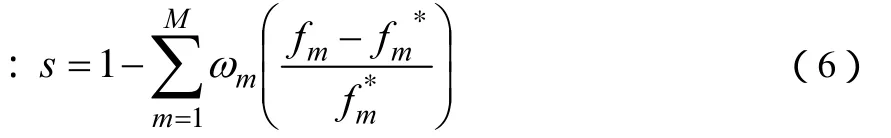
其中，mω为惯性权重，用来调节距离、时间、费用三个优化目标的相对重要性，为第m个指标的理想解，fm为多目标优化得到的第m个指标的解。我们把满意度较高的解称为满意解。

3 TSP模型在永州市物流配送设计中的应用

3.1 模型的实例研究

为了突出配送点的代表性，我们以冷水滩区为中心，构造向其他区县配送的车辆调度和运输路线。对各区县的编号如下：1、冷水滩，2、零陵，3、祁阳，4、东安，5、双牌，6、道县，7、宁远，8、江永，9、江华，10、新田，11、蓝山。

实验中我们假设以汽车为交通工具，交通道路以国道公路和省道公路为主。基于GPS，得到11个区县距离矩阵如D所示：

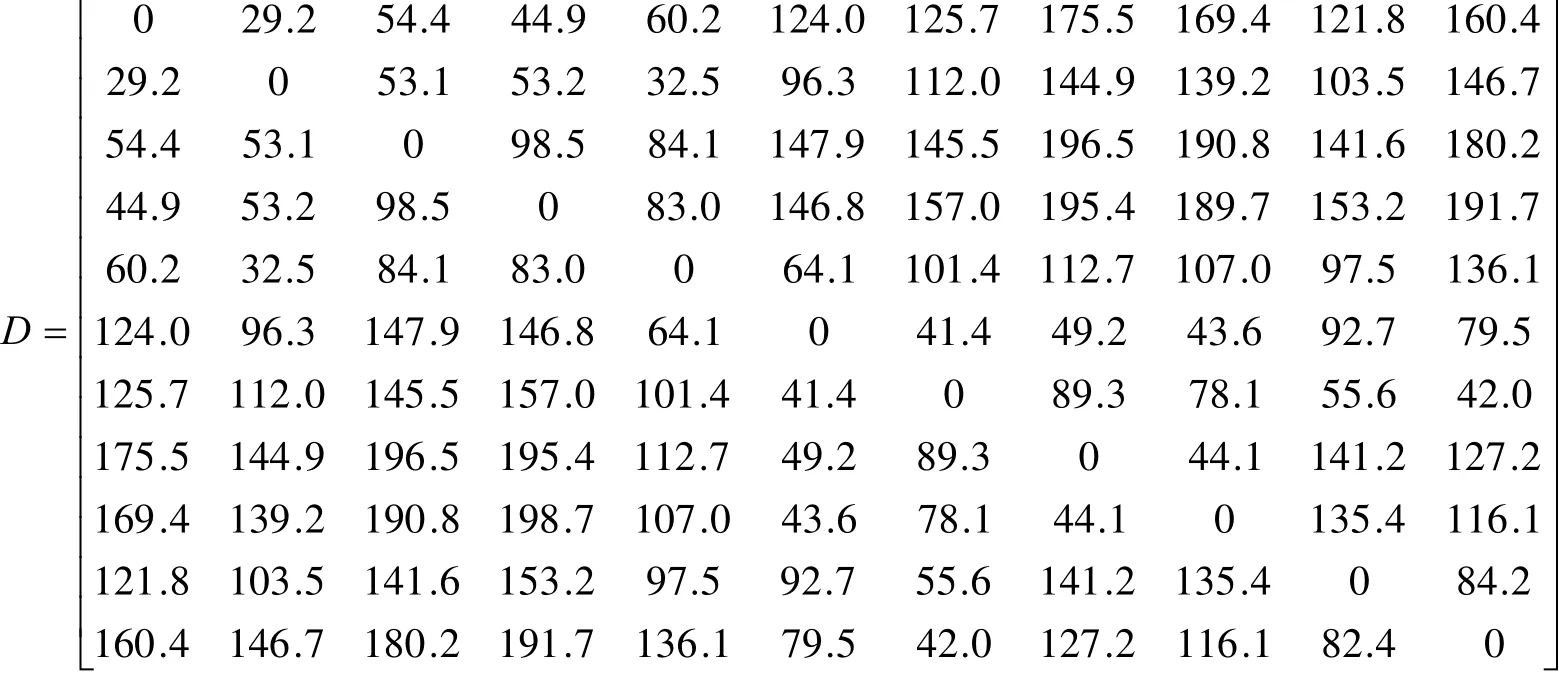
两两配送点之间的费用主要由交通、餐饮和住宿所产生，由于餐饮、住宿的不确定性因素很大，可以估算出总费用并将其平均到每个边上，这样每个边的餐饮、住宿费用与所访问的城市次序无关，而交通费用与公路等级有关，因此我们只考虑交通费用，按照国道公路1.0元每公里，省道公路0.5元每公里，结合距离矩阵，估算出交通费用如矩阵C所示：

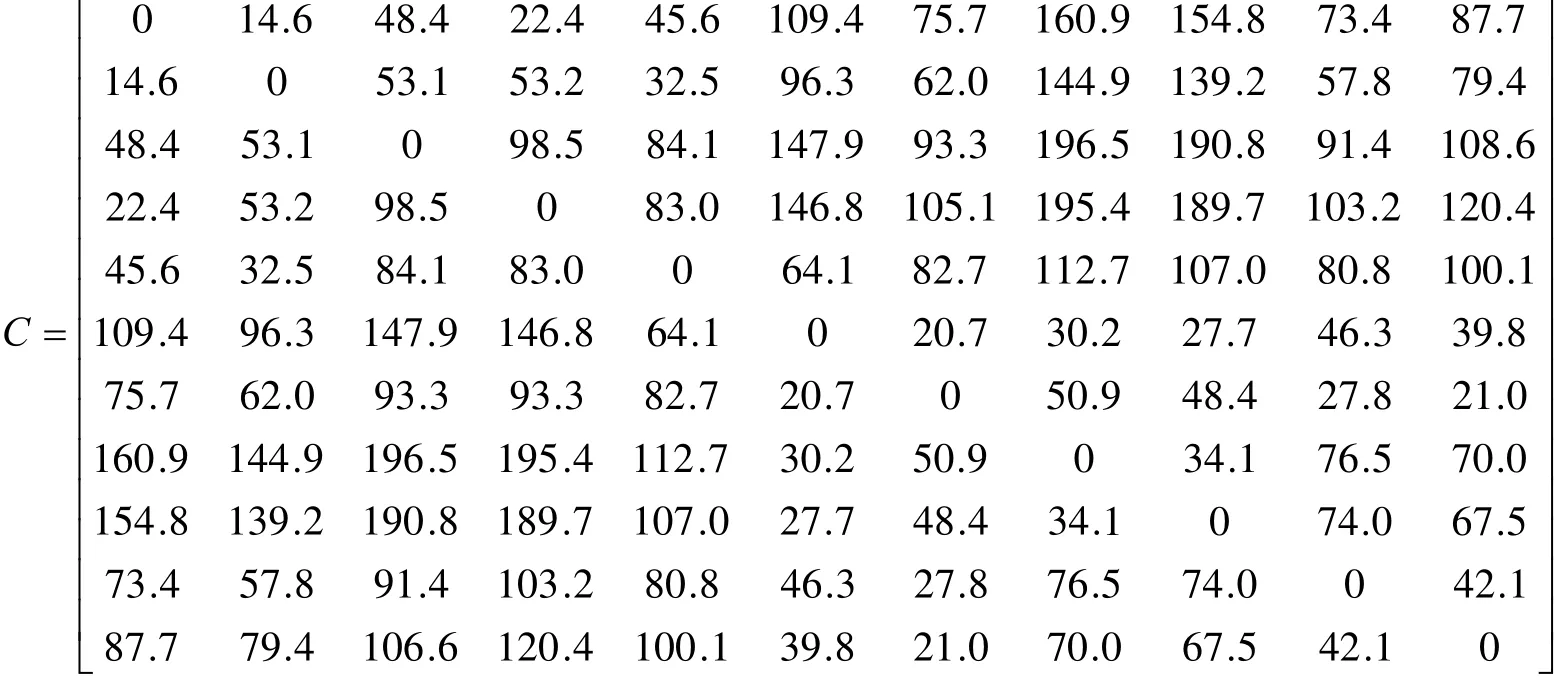
由于把路况分为平地和山区两种，我们假设平地路段汽车行驶速度为80公里/小时，山区路段行驶速度50公里/小时估算时间，得到时间矩阵如T所示：

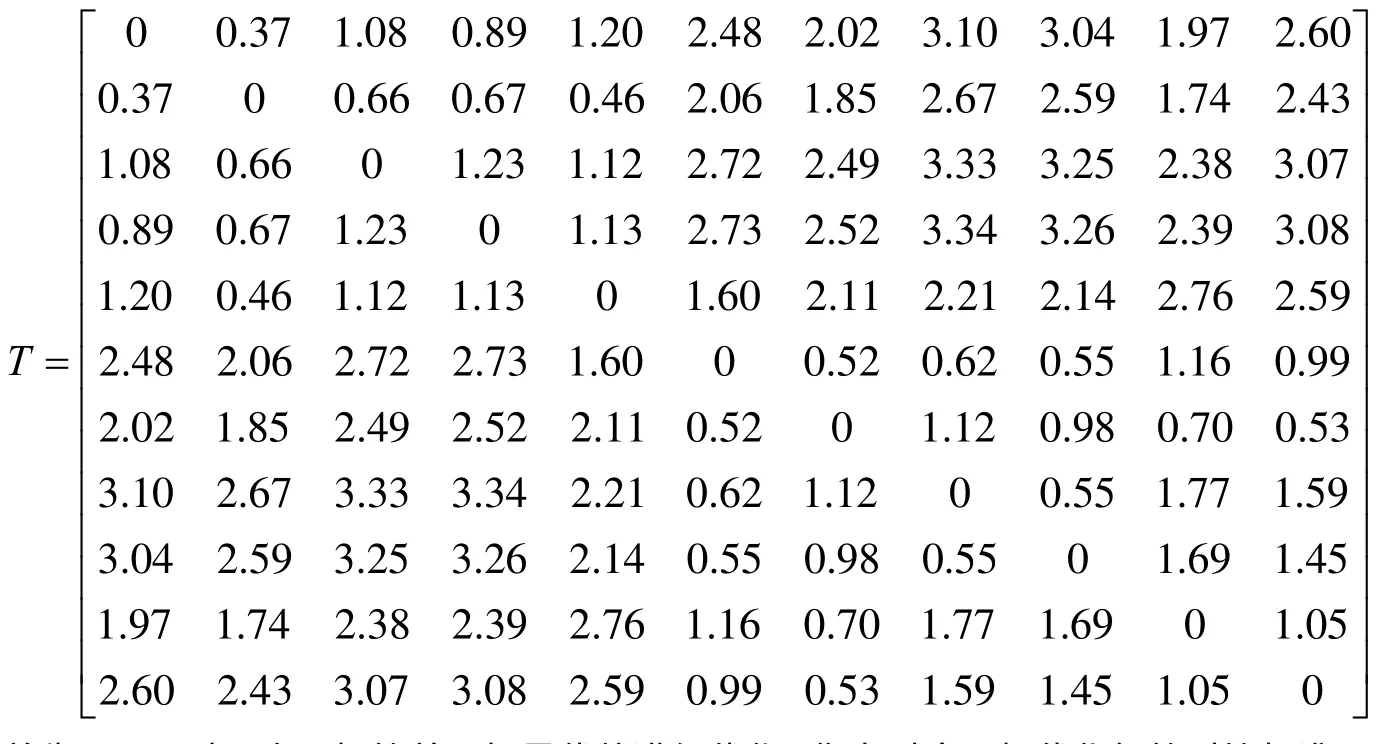
首先用PSO对三个目标的单目标最优值进行优化，作为对多目标优化解的对比标准，即理想解。三个单目标最优值如下：

以距离最短为目标，最短距离为628.6公里，配送点访问次序为：1-3-4-2-5-6-8-9-10-7-11

以费用最少为目标，最少费用为472.5元，配送点访问次序为：1-4-3-2-5-6-9-8-7-11-10

以时间最短为目标，最少时间为9.05小时，配送点访问次序为：1-3-4-2-5-6-8-9-7-11-10．

两目标优化时，令两个惯性权重相等，都为0.5，结果如表3.1、表32和表3.3所示：

表3.1 以距离和时间为目标的Pareto最优解集

表3.2 以距离和费用为目标的Pareto最优解集

表3.3 以时间和费用为目标的Pareto最优解集

三个目标一起优化时，惯性权重的选择不同会产生不同的优化结果，取三个权重均分区间[0,1]，即，1ω=0.33，2ω =0.33，3ω =0.34，得到Pareto最优解如表3.4所示：

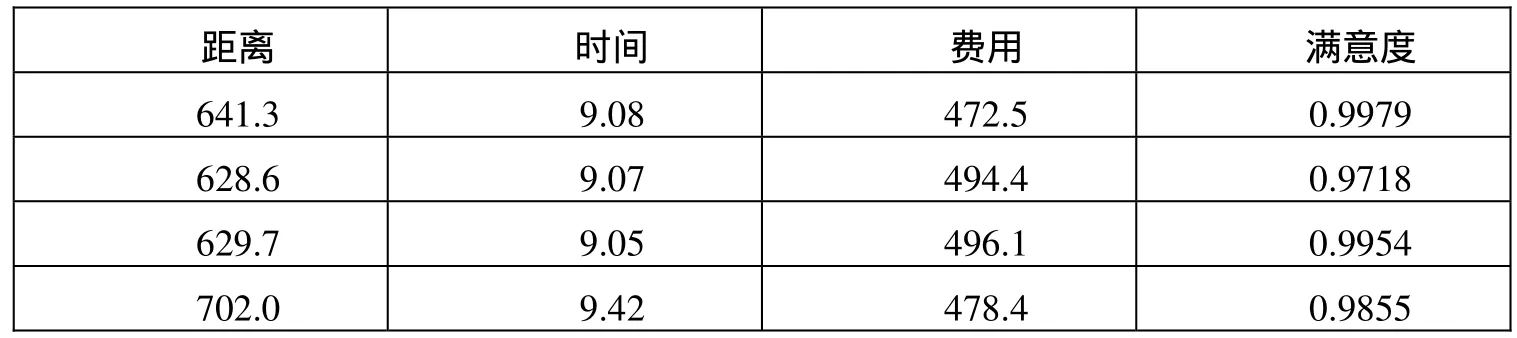
表3.4 三个目标优化的Pareto最优解集

其中，满意度最高的解对应的景点访问次序为：1-4-3-2-5-6-9-8-7-11-10，对应的景点顺序为：

冷水滩—东安—祁阳—零陵—双牌—道县—江华—江永—宁远—蓝山—新田。

3.2 模型分析

该模型是基于多目标的TSP问题的数学模型，它主要针对于当前对单目标研究运输线路中的不足而提出来的，其综合考虑了距离、时间、费用等因素在模型中的影响，并根据满意度评价模型而获得综合Pareto最优解。最后，我将该模型应用到永州市物流配送中心车辆调度和运输路线的优化系统中，实现了部分功能，对永州市l1个区县进行了时间、距离、费用的目标优化，得到了较满意的Pareto最优解。为永州市的物流配送中心车辆调度和运输路线的优化提供了理论依据和实用价值。但是，该模型还存在着很多不足之处，主要表现在如下：

（1）模型中权重系数没有一个精确地确定方法；

（2）对求多目标模型的考虑因素还不全面，例如交通堵塞、天气影响行程等。

（3）由于永州市的区县较多，因此建模时考虑的配送点数也较多，没有考虑配送过程中的休息，有一定的局限性。

如不考虑单线路配送，而考虑分组配送的话应可得到更优化的配送线路。

4 结束语

物流中心配送路径优化问题是一个典型的车辆路径问题，属于NP—Complete问题之一。随着节点数的增加，计算量将迅速增大，运用计算机工具和GPS信息是必不可少的。本文根据物流中心的实际情况，对物流中心的配送问题进行了相对简单的模型建立和简化，基于GPS信息灵活运用TSP的求解方式，来解决物流配送中心的车辆分配和运输路径的优化，得到相对较为优化的方案。

[1]齐少安,宋齐军.基于TSP模型的物流配送中心车辆路径优化[J].邮电设计技术,2006,6,（6）:62-64.

[2]苏晋荣.基于智能优化算法的TSP问题研究及应用[D].山西:山西大学学报,2007,5,22.

Based multi-objective TSP model’s application in Yongzhou city’s logistic distribution

Wei Mei-yan
(Dept. of Computer and Communication engineering, Hunan University of Science and Engineering, YongZhou, 425100, China)

In this paper, from the perspective of logistic center, we take Yongzhou City as an example. To distance, time, cost of indicators, adopting branch and round method to set up a multi-objective TSP model. Afterwards using based PSO algorithm satisfaction of degree model to evaluate satisfaction of degree, got the best design scheme of transportation routes, then provided a theoretical basis and reference for logistic center in mathematical model.

Transportation routes; TSP model; PSO algorithm; logistic distribution

TP39

A

1673-2219（2012）08-0035-04

2012－04－20

项目资助：永州市科技计划项目。

韦美雁（1974－），女，湖南永州人，副教授，硕士，主要从事应用软件和地理信息系统研究。

（责任编校：何俊华）