平面简谐波势能的简易分析方法

汪新文 唐世清 许成科 陆世专 王文炜

(衡阳师范学院 物理与电子信息科学系，湖南 衡阳 421008)

平面简谐波势能的简易分析方法

汪新文 唐世清 许成科 陆世专 王文炜

(衡阳师范学院 物理与电子信息科学系，湖南 衡阳 421008)

平面简谐波是理工科专业《大学物理》课程中的重要内容。势能的分析和推导是平面简谐波教学中的难点。本文利用弹性波的传播机理和特征，提出一种简易的分析和推导平面简谐波势能密度函数的方法。此方法可以避开学生陌生和难以理解的一些物理量和概念，因此其可使教学过程大为简化，并便于学生掌握和深刻理解相关内容。

平面简谐波；势能函数；分析方法

1 引言

近些年来，由于各种原因，大学课程门类不断增加，大学生学习负担也不断加重。因此，各门传统课程（包括专业课和公共课）的课时数大幅减少。作为理工科学生必修的一门公共课，《大学物理》的课时也不例外地被大幅削减。而另一方面，地方二本院校的学生的物理和数学基础呈下滑趋势。在这种背景下，《大学物理》课程在教学内容和教学方式方法等方面都必须进行改革。教师在教学过程中应更加注重对学生物理思维的培养、把复杂问题尽量简单化，在备课时应积极探索相关定理、定律及其数学表示的尽可能简易的分析和推导方法，才可能达到既节约课时又提高教学质量和效果的目的。

平面简谐波是《大学物理》课程中的重要内容。为了揭示机械波是振动状态和能量传播的本质，需要分析和讨论介质中各质元和一定体积内的机械能及其随时间的变化情况。动能关于时间的函数可以直接从波动方程导出，所以比较简单。势能是由介质内各体积元的形变而产生的，其大小与形变的程度有关，分析起来要复杂些。几乎所有的教材和文献[1-5]都是利用胡克定律来推导势能密度函数。这种方法涉及到应力、弹性模量、切变模量等概念以及它们之间的关系，然而这些内容超出了教学大纲，教材中也都没有相关详细介绍。鉴于此，多数教材中都把势能函数的推导过程放在附录中或列为选讲内容。由于课时的限制，教师在教学过程中通常直接给出势能公式，这样严重影响学生对机械波的能量传播的深刻理解。

本文充分利用弹性波的传播机理和特征，以及谐振子与平面简谐波之间的关系，提出一种简易的分析和推导平面简谐波势能密度函数的方法。由于此方法没有涉及到应力、弹性模量、切变模量等学生陌生和难以理解的“新”概念和物理量，其不仅可使课堂教学过程变得流畅，更便于学生掌握和深刻理解传播机械波的媒质中各部分体积元的能量的变化规律。

2 平面简谐波的势能分析

机械波是机械振动在连续介质中的传播，即是振动状态和能量的传播，当机械波在介质中传播时，体积元（作机械振动）的机械能是不守恒的。然而，由波动的周期性可知：体积元的机械能在一个周期内的平均值应该是不变的。如果取各向同性介质中的单位体积为质元，并把其视为质点，则其在一个周期内的平均机械能在形式上应该与相应的谐振子系统的平均机械能相类似。

下面，我们把上述思想运用到平面弹性简谐波的能量分析中，并非常简单地导出平面简谐波的势能密度（单位体积内的势能）。设平面简谐波的波动方程为

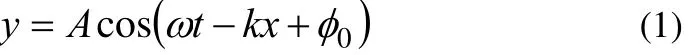
式中 A为振源及各质元的振幅，ω为波的圆频率，k 为波矢，x是与一条波线（传播方向）重合的坐标轴，0φ是坐标原点处质元的振动初相位。此平面简谐波的动能密度（单位体积内的动能）为

式中ρ为介质的密度。由 (2) 式可得一个周期T内的平均动能密度

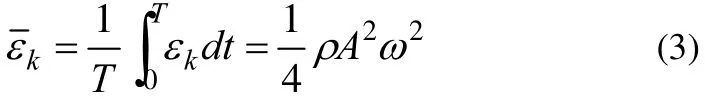
由 (3) 和 (4) 式可得此平面简谐波在一个周期内的平均势能密度

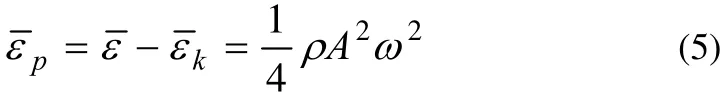
很显然，平面简谐波在一个周期内的平均势能密度与平均动能密度相等。

现在分析任意时刻的势能密度εp。由 (5) 式可得εp必须满足如下条件：

由弹性波的传播机理可知：体积元的势能和动能应同时变大、同时变小；在平衡位置时同时达到最大值，在位移绝对值最大位置时同时达到最小值。这里以在绳上传播的横波为例来证实上述的结论。如图1所示，横波在绳上传播时，

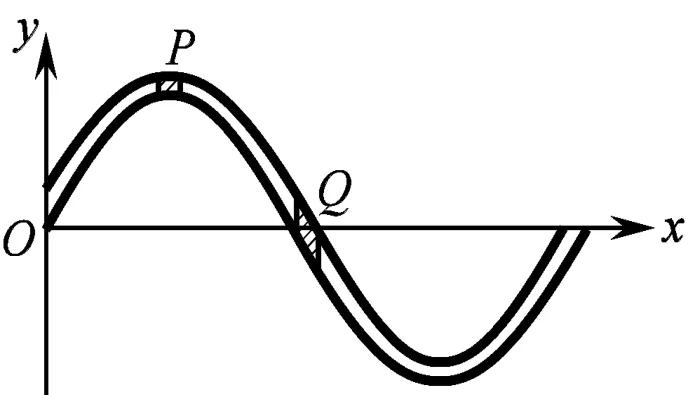
图1：横波在绳上传播的示意图

平衡位置Q处体积元的速度最大因而动能最大，此时Q处体积元的相对形变也最大，因此弹性势能也为最大；在振动位移最大的 P处体积元，其振动速度为零，动能等于零，而此处体积元的相对形变量为最小值其弹性势能亦为零；更一般地，体积元的动能变大或变小时，势能也相应地变大或变小，反之亦然。根据上述分析可得：平面简谐波的势能密度与动能密度同相。因此，

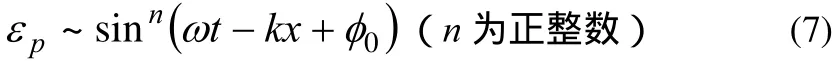
而由 (6) 的条件可得n=2，且有

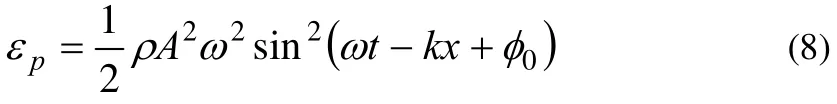
此结果正是正确的势能密度函数，其与动能密度函数完全相同。根据势能密度函数就可以分析平面简谐波在单位体积内的势能随时间的变化情况。

3 总 结

本文根据谐振子与平面简谐波之间的关系，并把媒质中单位体积元视为质点，利用类比的方法得到了平面简谐波在一个周期内的平均能量密度，进而得到了平均势能密度。然后利用弹性波的传播机理和特征，即媒质中体积元的动能与势能同相，导出了平面简谐波的势能密度函数。此思路和方法没有借助胡克定律，从而没有涉及到应力、弹性模量、切变模量等学生陌生和难以理解的物理量。因此，本文中的方法不仅可以节约课堂时间，又可使课堂教学过程变得流畅，更便于学生掌握和深刻理解相关内容。

[1]匡乐满,等.大学物理:第二册[M].北京:北京邮电大学出版社,2007.

[2]陈曙光,等.大学物理学:上册[M].长沙: 湖南大学出版社,2006.

[3]赵近芳,等.大学物理学:上册[M].北京: 北京邮电大学出版社,2011.

[4]叶帆.关于连续介质中横波的能量探讨[J].大学物理,2008,27(9):19-21.

[5]郭芳英,闫夷平,李爱玲.用横波推导简谐波的能量[J].物理与工程,2003, 12(2): 16-17.

Simple method for analyzing the potential energy of a simple harmonic plane-wave

WANG Xin-wen, TANG Shi-qing, XU Cheng-ke, Lu Shi-zhuan, Wang Wen-wei
(Department of Physics and Electronic Information Science, Hengyang Normal University, Hengyang 421008, China)

Simple harmonic plane-wave is an important content of《College Physics》course which is a required course for the students of science and engineering specialties. It may be not easy for students to deeply understand the potential energy during the study of the simple harmonic plane-wave. This paper proposes a very simple method of analyzing and deriving the potential energy,by using the transmission mechanism and characteristics of the elastic wave. This method does not involve the physical quantities that are unfamiliar to students, and thus can simplify the teaching process and benefit the students in understanding the related contents.

simple harmonic plane-wave; potential energy; analyzing method

O4-3

A

1673-2219（2012）08-0022-02

2012－05－20

衡阳师范学院教改项目(编号：jy201101)、教育部第一类特色专业(物理学)、湖南省“光电课程组”教学团队、湖南省“十二五”重点建设学科资助。

汪新文 (1980－)，男，湖南衡阳人，衡阳师范学院物理与电子信息科学系副教授，博士，主要从事量子光学与量子信息科学以及《大学物理》等课程的教学改革研究。

（责任编校：何俊华）