天然肠衣搭配问题的优化模型研究
2012-12-08夏英
夏 英
(海南工商职业学院基础课部,海南海口 570203)
天然肠衣搭配问题的优化模型研究
夏 英
(海南工商职业学院基础课部,海南海口 570203)
以2011年全国大学生数学建模竞赛D题为背景,针对天然肠衣搭配问题建立了双目标规划模型及整数规划模型,采用了“三步走”方法对模型进行简化,为制定出“照方抓药”的搭配方案提供了重要思路。
天然肠衣;双目标规划;整数规划;分组搭配
一 问题的提出
考虑如下天然肠衣搭配问题。天然肠衣的原料按长度分档,通常以0.5米为一档,如:3-3.4米按3米计算,3.5米 -3.9米按3.5米计算,其余依此类推。为提高生产效率,公司计划改变组装工艺,先丈量所有原料,建立一个原料表,数据来源2011年全国大学生数学建模竞赛D题附表[1]。根据以上成品和原料描述,设计一个原料搭配方案,工人根据这个方案“照方抓药”进行生产。公司对搭配方案有以下具体要求:
(一)对于给定的一批原料,装出的成品捆数越多越好;
(二)为提高原料使用率,总长度允许有±0.5米的误差,总根数允许比标准少1根;
(三)某种规格对应原料如果出现剩余,可以降级使用。如长度为14米的原料可以和长度介于7-13.5米的进行捆扎,成品属于7-13.5米的规格。建立上述问题的数学模型,给出求解方法。
二 问题的分析
首次按将46种原材料进行依次编号,每种原材料的长度按要求规范化,并将三种成品的原材料进行了分组(见表1、2、3)。在已知成品标准和原料规格的情况下[2,3],制定出符合多种要求的搭配方案,故其实质是一个优化问题。本文建立了双目标规划模型及整数规划模型[4],采用了“三步走”方法对模型进行分解,为制定出“照方抓药”的搭配方案提供了重要思路。

表1 产品一原料描述表

表2 产品二原料描述表
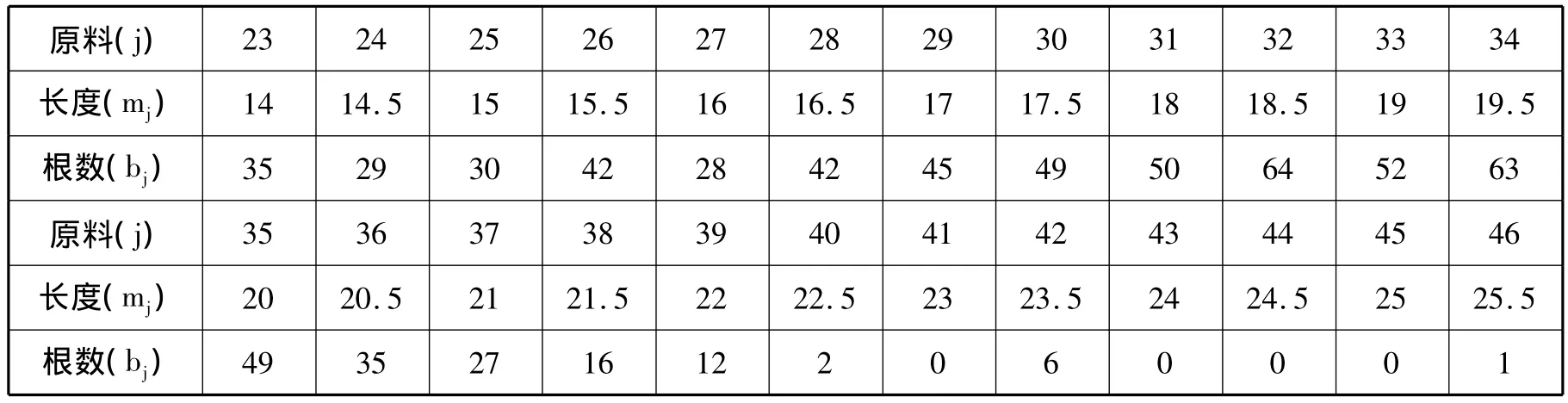
表3 规格要求产品三原料描述表
三 基本假设
(一)假设原材料1—8号生产成品一,9—22号生产成品二,23—46号生产成品三;
(二)假设在计算成品时允许总长度有0.5米的误差;
(三)假设允许计算成品时总根数比标准少一根;
(四)假设某种规格对应原料如果出现剩余,可以降级使用。降级使用时为避免余料浪费过多,将余料统一降级到下一个等级中的最大档使用。
四 双目标规划的模型建立与求解探讨
(一)双目标规划模型的建立
1.双目标规划模型的目标函数和约束条件的分析
(1)先考虑目标函数
用Z表示三种成品i的总捆数,Zi表示成品i的捆数,为使给定的原材料最大程度得到利用,组装出的成品捆数越多越好,即要实现目标一:

另一方面,用F表示三种成品i的总误差和,δi表示Zi捆成品i的误差和,要求余料越少越好,最大程度减少原料浪费,即要实现目标二:

(2)约束条件分析
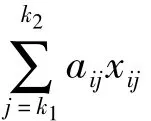

其中:
aij表示制作成品i所需要的第j种原材料1根的长度;当 i=1时,k1=1,k2=8;当i=2时,k1=9,k2=22;当 i=3 时,k1=23,k2=46。
②为提高原材料使用率,每捆要求总长度允许有±5米的误差,从而Zi捆成品i的误差和δi的绝对值应该小于每捆误差要求0.5米的捆数Zi倍。那么:

③采用第j种原材料制作第i种成品的根数xij应该不多于第i种原材料的总根数bj,那么:
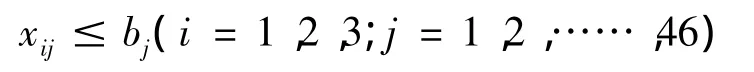


⑤整数非负限制
显然需要 xij≥0(i=1,2,3;j=1,2,…,46)并且取整数。
2.双目标规划模型的建立
由此可得到一个双目标优化模型:


其中:
当 i=1 时,k1=1,k2=8;当i=2 时,k1=9,k2=22;当 i=3 时,k1=23,k2=46.
3.双目标规划模型的求解探讨

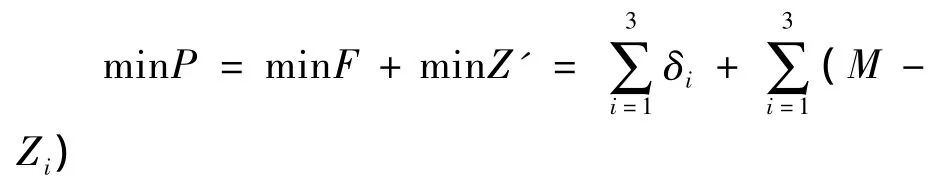

其中:
当 i=1 时,k1=1,k2=8;当i=2 时,k1=9,k2=22;当 i=3 时,k1=23,k2=46.
鉴于上述模型用数学软件Matlab编程的难度比较大,实际操作难以实现。于是进一步改进思路,采用“三步走”方法实现模型简化。

3 )可以具体转化为。于是,由模型(2)可以得到生产一捆成品三的单目标规划模型:


借助于数学软件Matlab,对上述模型(3)进行编程可以得到成品三搭配成一捆的搭配方案。同样,可以取i=1,2,求出成品一、二搭配成一捆的搭配方案。
第二步:先对成品三按照搭配一组的最优成捆方案进行“照方抓药”,直到有某种原材料短缺,无法再组装搭配下一捆为止。再将成品三的余料汇总,全部作降级处理,为避免浪费太大,全部降级到成品二的原材料中的最长档使用。按照这种思路接着搭配处理成品二、成品一。
第三步:最后将三种“照方抓药”成品i的捆数Zi求和,就得到了三种成品的总捆数Z。
(二)整数规划模型的建立与求解探讨
1.整数规划模型的目标函数和约束条件的分析
(1)先考虑目标函数

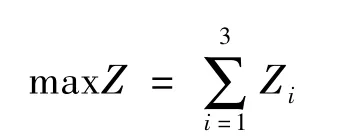
(2)再考虑约束条件
①由于天然肠衣每一种规格成品的长度是89米,那么对于捆数为Zi的第i种成品的总长度为89Zi,这正好就是制作的成品i采用原料j的长度与采用次数的乘积。而每捆要求总长度允许有±5米的误差,故1捆成品i的长度应该介于88.5~89.5米之间。那么Zi捆成品i总长度的范围为:

其中:
aij表示制作成品i所需要的第j种原材料1根的长度;
当 i=1 时,k1=1,k2=8;当i=2 时,k1=9,k2=22;当 i=3 时,k1=23,k2=46.
②采用第j种原材料制作第i种成品的根数xij应该不多于第种原材料的总根数bj,并且根数xij应该是非负数整数,那么:
x ij≤ bj(i=1,2,3;j=1,2,…,46),xij≥ 0且取整数


注:当 i=1时,k1=1,k2=8;当i=2时,k1=9,k2=22;当 i=3 时,k1=23,k2=46。
④成品i所取原料的总根数ni除以每种成品要求成捆的根数mi后取整就是成品i的捆数Zi(Zi为非负的整数)。而题中允许每捆成品i成捆时可以少一根,那么:
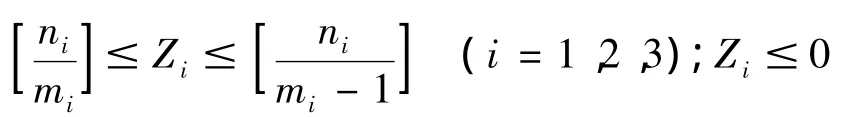
且取整数
2.整数规划模型的建立
由此可得到一个整数规划模型[6]:

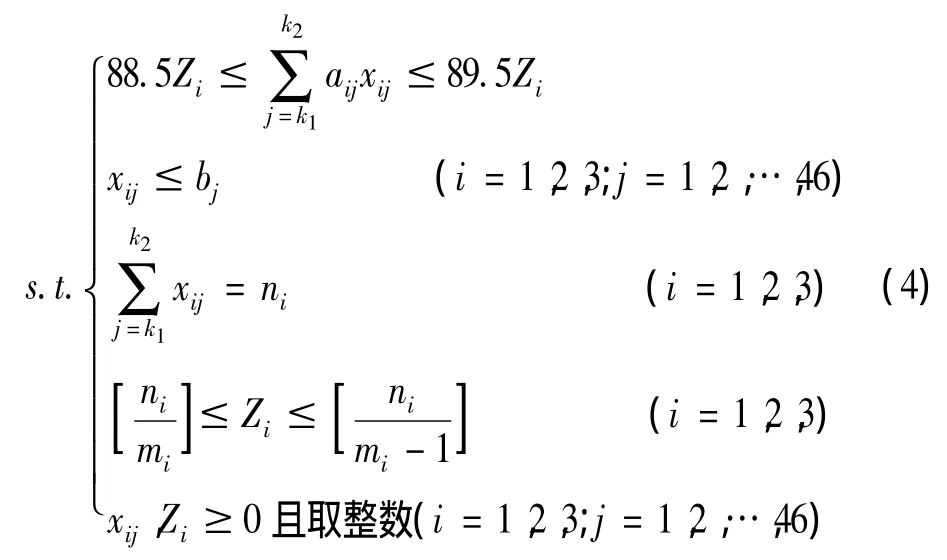
其中:
当 i=1 时,k1=1,k2=8;当i=2 时,k1=9,k2=22;当 i=3 时,k1=23,k2=46。
3.整数规划模型的求解探讨
由于上述模型综合考虑了三种规格的成品以及约束条件,对于求解比较复杂,为了简便起见,对三种规格的成品分组进行求解。在目标函数中要求成品捆数越多越好,这里可以理解为:每种规格的成品捆数都达到最大时,总捆数Z也达到最大。运用这个想法,对于三种规格的成品分别建立相应的整数规划模型。



同理可以分别针对成品二、成品一构建类似的整数规划模型,运用Matlab软件可以求得三种成品的成捆的各自最大捆数Zi。当三种成品的捆数Zi均达到最大值,那么对于给定的这批原料,装出成品的总捆数Z就最大。
五 模型的评价与改进
(一)模型的优点
1.模型针对天然肠衣搭配问题构建了两个优化模型,全面地考虑题目中的各种要求;
2.模型结构清晰、层次分明、数学表达式含义直观、易懂;
3.巧妙将模型一由原来双目标规划问题转化为单目标规划问题,并针对该模型提出“三步走”策略,将模型一的编程求解难度大大降低。同时巧妙地将模型二按照生产产品的种类分解开,将模型二的编程求解难度大大降低;
4.此模型可推广应用于材料切割、材料的优化搭配选取、制定批量生产与存储问题、企业的各项管理活动等方面。
(二)模型的缺点
1.在成品原料分组的情况下分析解决问题,使得某些长的原料因为无法与该组的其他原料有效组合,导致在该轮组装中被迫降级使用,造成不必要浪费;
2.两个模型的算法思路很好,但是算法实现耗时太长,对于30分钟内产生最优搭配方案有一定难度。
(三)模型的改进
模型在此基础上考虑结合其他优化方法和决策控制知识作进一步改进。
[1]2011 高教社杯全国大学生数学建模竞赛组委会[EB/OL].http://www.mcm.edu.cn/html_cn/node/a1ffc4c5587c8a6f96eacefb8dbcc34e.html.
[2]朱锦林.天然肠衣加工指南[M].北京:中国计量出版社,2009.
[3]刘德明.肠衣的生产与加工[J].甘肃畜牧兽医,1985(2).
[4]姜启源.数学模型(第二版)[M].北京:高等教育出版社,1993.
[5]朱道元.数学建模精品案例[M].南京:东南大学出版社,1999.
[6]教材编写组.运筹学(第三版)[M].北京:清华大学出版社,2005.
Study on the Optimal Models of the Tie-in Problem of Natural Casing
XIA Ying
(Department of Basic Courses,Hainan Technology and Business College,Haikou 570203,China)
The article is based on the 2011 Mathematical Contest in Modeling D(MCM)of China.It sets up a dual- goal programming model and integer programming model for the natural casing tie-in problem,and uses the"three-step"method to simplify the models,providing referential ideas for working out a"fill a prescription as"match scheme.
Natural casing;Dual-goal programming;Integer pro;Block matching
O 224
A
1009-9743(2012)01-0149-05
2011-12-15
夏英(1975-),女,汉族,湖南岳阳人。硕士。海南工商职业学院基础课部讲师。主要研究方向:运筹学。
(责任编辑:张玉秀)
